A very helpful method for understanding the operation of proportional, integral, and derivative control terms is to analyze their respective responses to the same input conditions over time.
This section is divided into subsections showing P, I, and D responses for several different input conditions, in the form of graphs. In each graph, the controller is assumed to be direct-acting (i.e. an increase in process variable results in an increase in output).
It should be noted that these graphic illustrations are all qualitative, not quantitative. There is too little information given in each case to plot exact responses. The illustrations of P, I, and D actions focus only on the shapes of the responses, not their exact numerical values.
Also Read : Two out of Three Logic Analogy
In order to quantitatively predict PID controller responses, one would have to know the values of all PID settings, as well as the original starting value of the output before an input change occurred and a time index of when the change(s) occurred.
Responses to a single step-change input
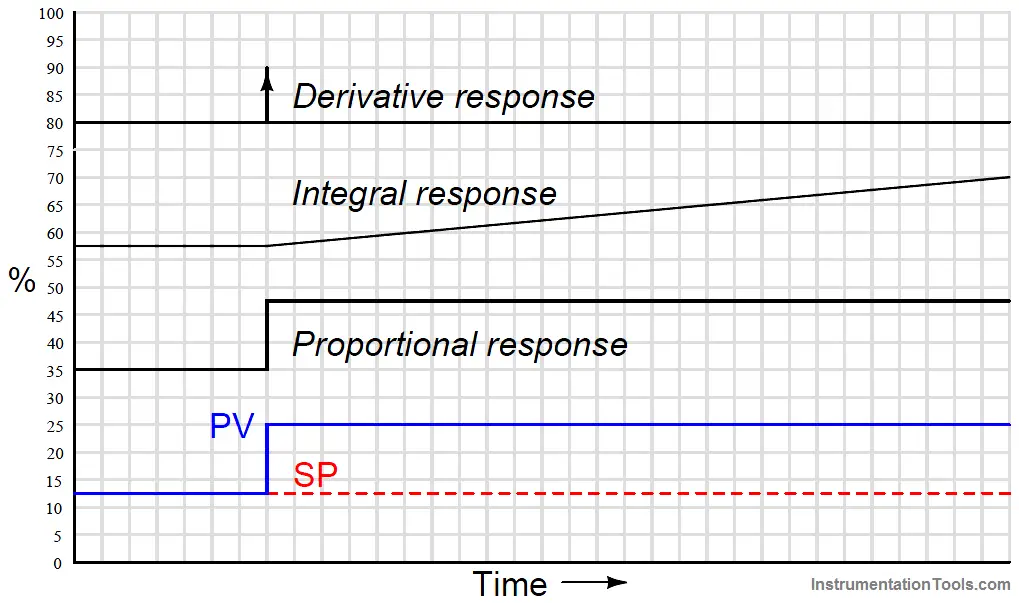
Proportional action directly mimics the shape of the input change (a step). Integral action ramps at a rate proportional to the magnitude of the input step.
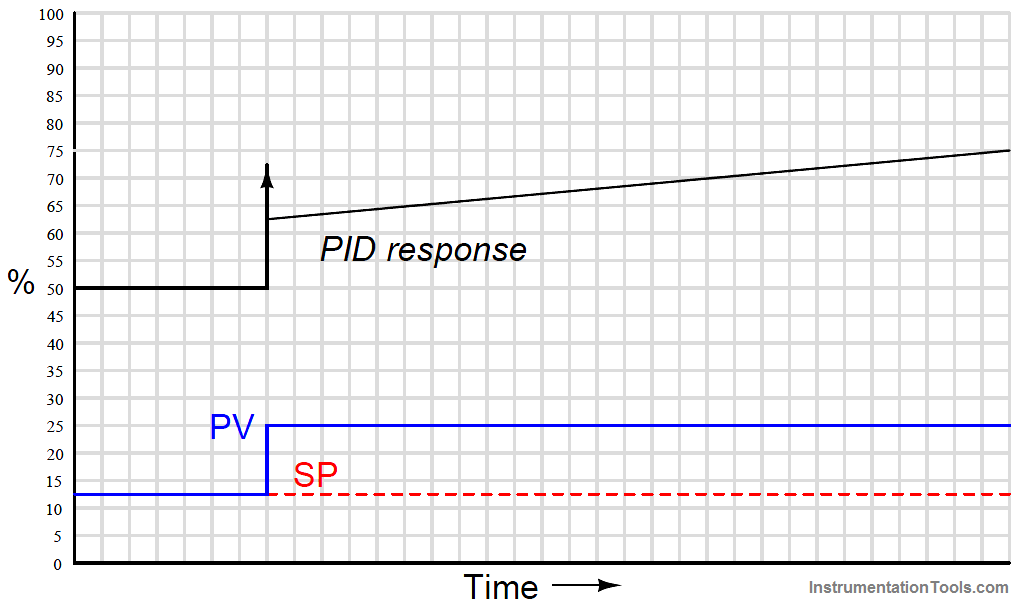
Since the input step holds a constant value, the integral action ramps at a constant rate (a constant slope). Derivative action interprets the step as an infinite rate of change, and so generates a “spike” (Note 1 ) driving the output to saturation. When combined into one PID output, the three actions produce this response:
Note 1 : This is the meaning of the vertical-pointing arrowheads shown on the trend graph: momentary saturation of the output all the way up to 100%.
Responses to a momentary step-and-return input
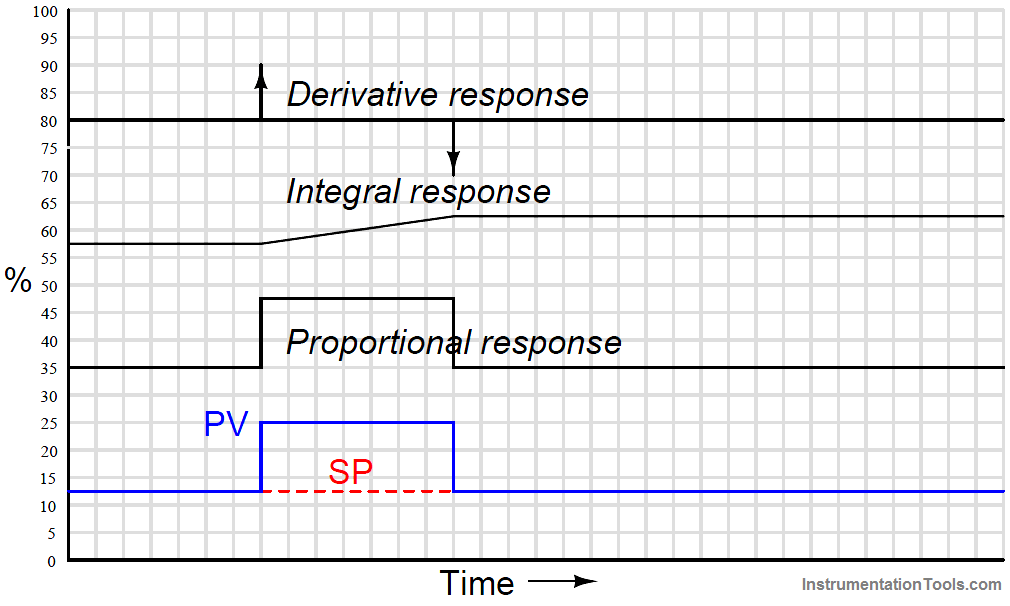
Proportional action directly mimics the shape of the input change (an up-and-down step).
Integral action ramps at a rate proportional to the magnitude of the input step, for as long as the PV is unequal to the SP.
Once PV = SP again, integral action stops ramping and simply holds the last value (Note 1 ).
Derivative action interprets both steps as infinite rates of change, and so generates “spikes” (Note 3 ) at the leading and at the trailing edges of the step.
Note how the leading (rising) edge causes derivative action to saturate high, while the trailing (falling) edge causes it to saturate low.
Note 2 : This is a good example of how integral controller action represents the history of the PV − SP error.
The continued offset of integral action from its starting point “remembers” the area accumulated under the rectangular “step” between PV and SP.
This offset will go away only if a negative error appears having the same percent-minute product (area) as the positive error step.
Note 3 : This is the meaning of the vertical-pointing arrowheads shown on the trend graph: momentary saturation of the output all the way up to 100% (or down to 0%).
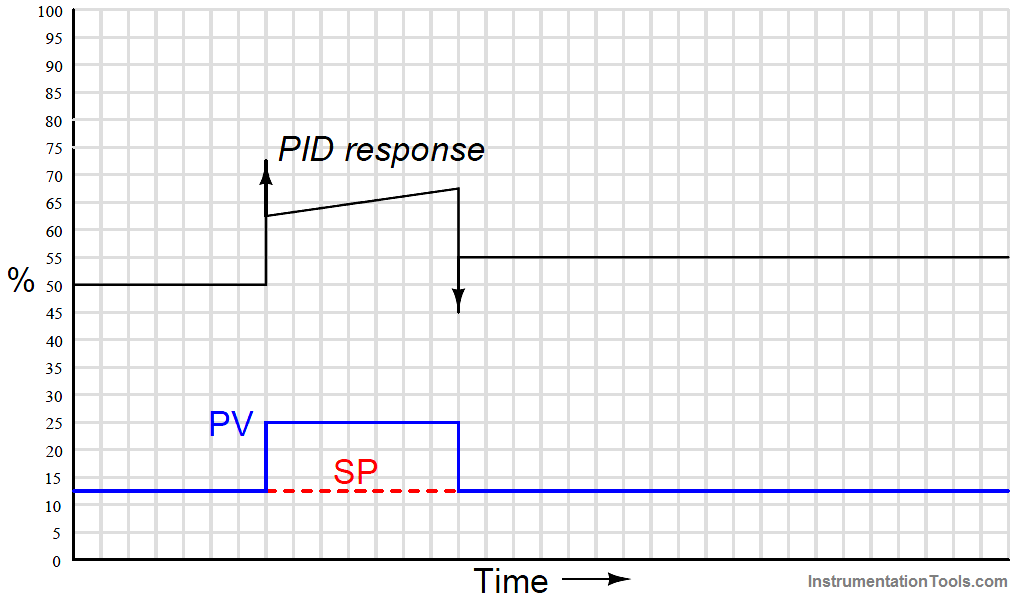
When combined into one PID output, the three actions produce this response:
Responses to two momentary steps-and-returns input
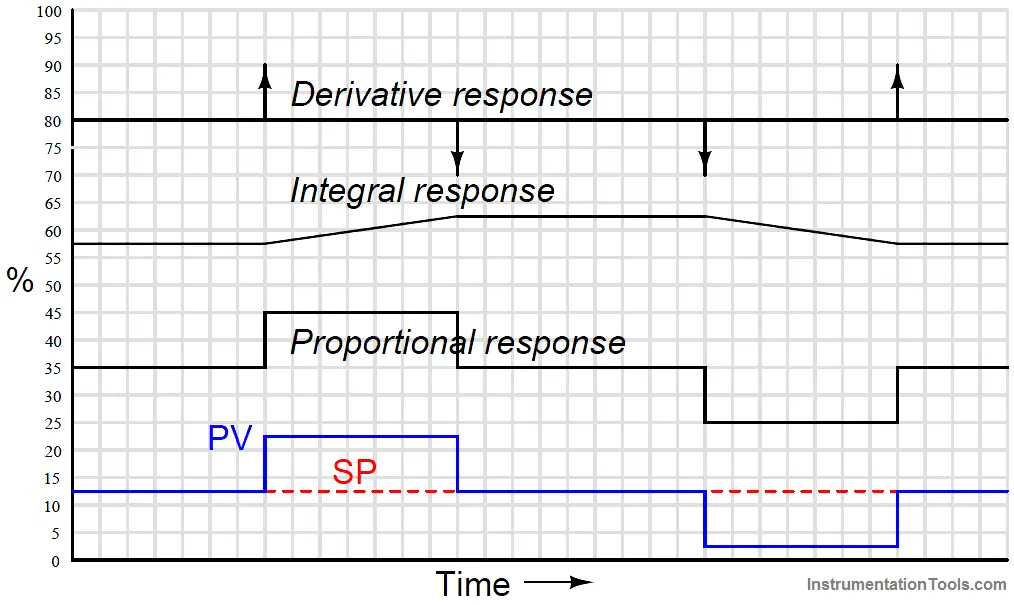
Proportional action directly mimics the shape of all input changes.
Integral action ramps at a rate proportional to the magnitude of the input step, for as long as the PV is unequal to the SP.
Once PV = SP again, integral action stops ramping and simply holds the last value.
Derivative action interprets each step as an infinite rate of change, and so generates a “spike” at the leading and at the trailing edges of each step.
Note how a leading (rising) edge causes derivative action to saturate high, while a trailing (falling) edge causes it to saturate low.
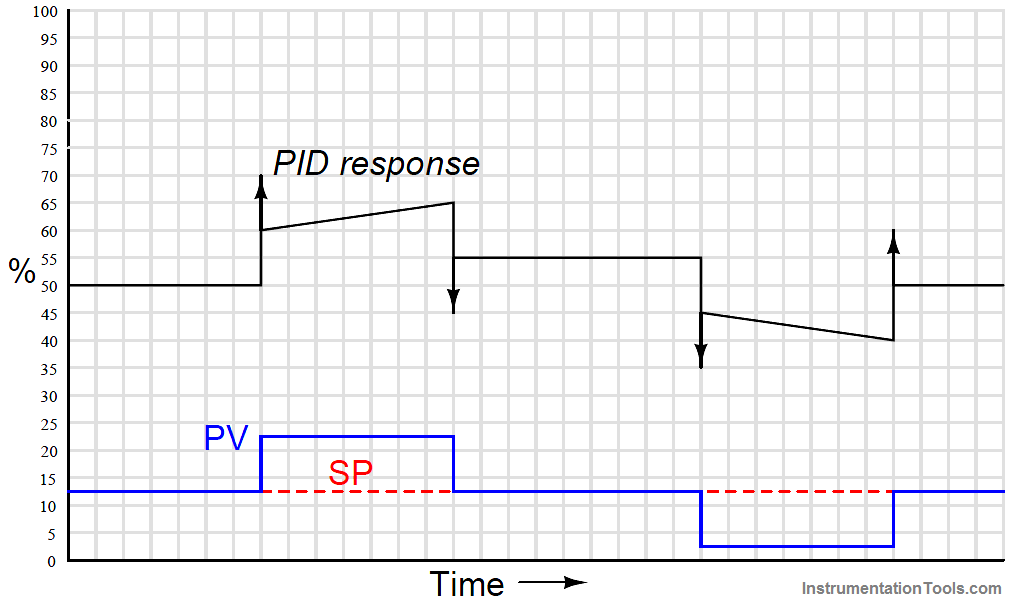
When combined into one PID output, the three actions produce this response:
Responses to a ramp-and-hold input
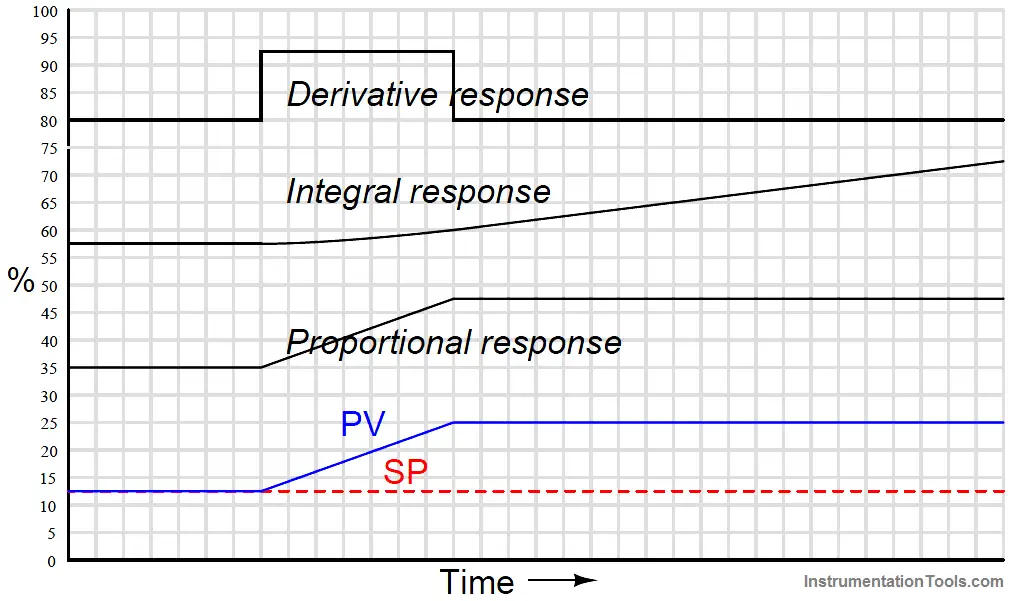
Proportional action directly mimics the ramp-and-hold shape of the input.
Integral action ramps slowly at first (when the error is small) but increases ramping rate as error increases.
When error stabilizes, integral rate likewise stabilizes. Derivative action offsets the output according to the input’s ramping rate.
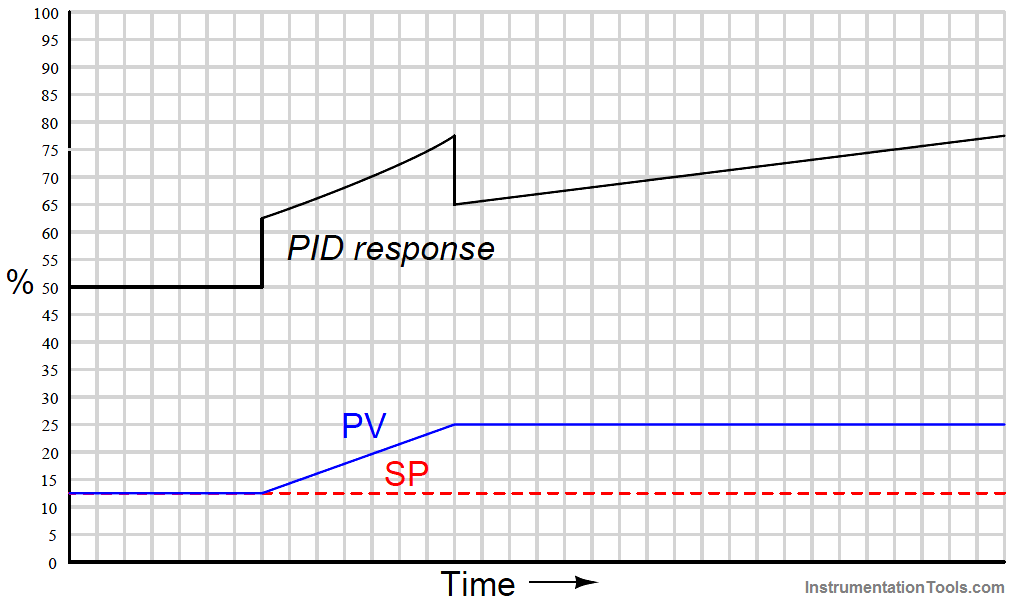
When combined into one PID output, the three actions produce this response:
Responses to an up-and-down ramp input
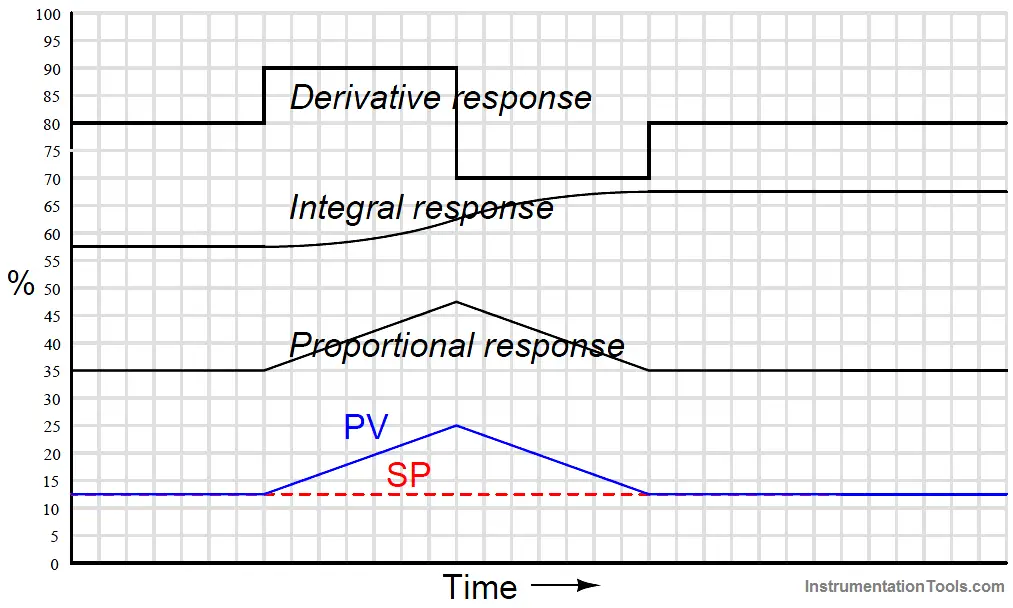
Proportional action directly mimics the up-and-down ramp shape of the input.
Integral action ramps slowly at first (when the error is small) but increases ramping rate as error increases, then ramps slower as error decreases back to zero.
Once PV = SP again, integral action stops ramping and simply holds the last value. Derivative action offsets the output according to the input’s ramping rate: first positive then negative.
When combined into one PID output, the three actions produce this response:
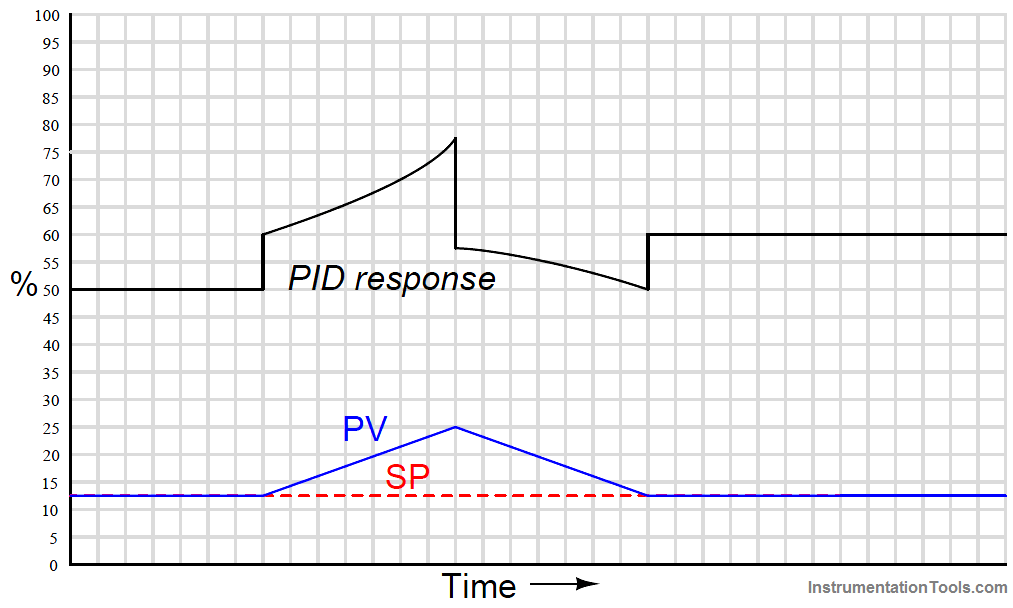
Responses to a multi-slope ramp input
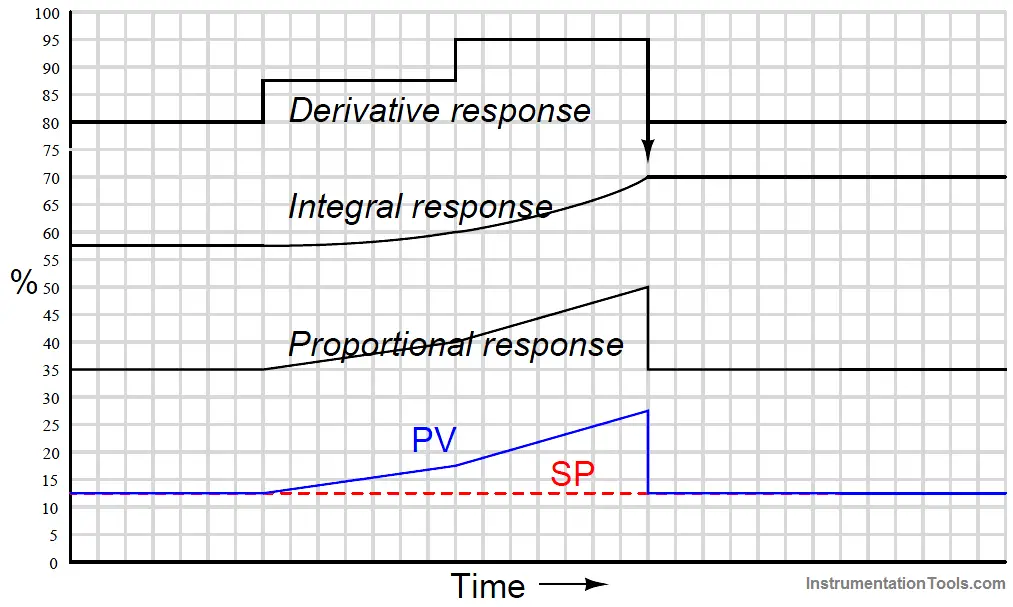
Proportional action directly mimics the ramp shape of the input.
Integral action ramps slowly at first (when the error is small) but increases ramping rate as error increases, then accelerates its increase as the PV ramps even steeper.
Once PV = SP again, integral action stops ramping and simply holds the last value.
Derivative action offsets the output according to the input’s ramping rate: first positive, then more positive, then it spikes negative when the PV suddenly returns to SP.
When combined into one PID output, the three actions produce this response:
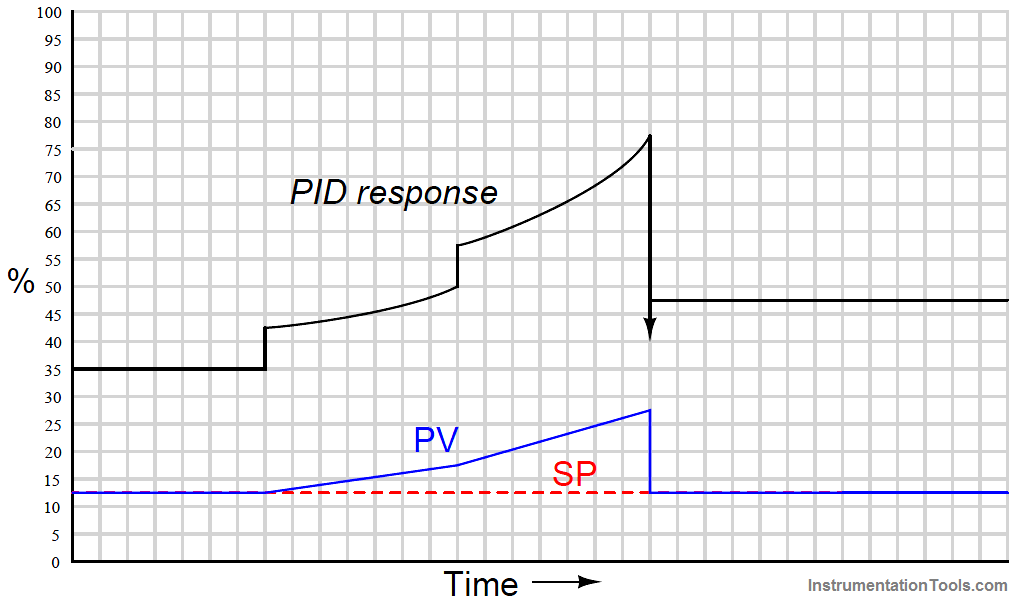
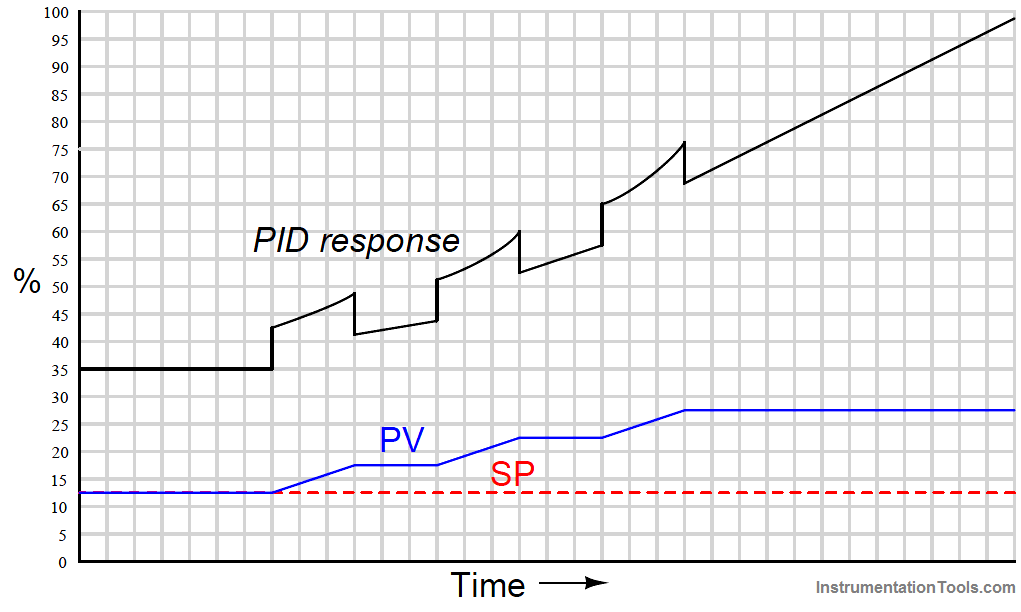
Responses to a multiple ramps and steps input
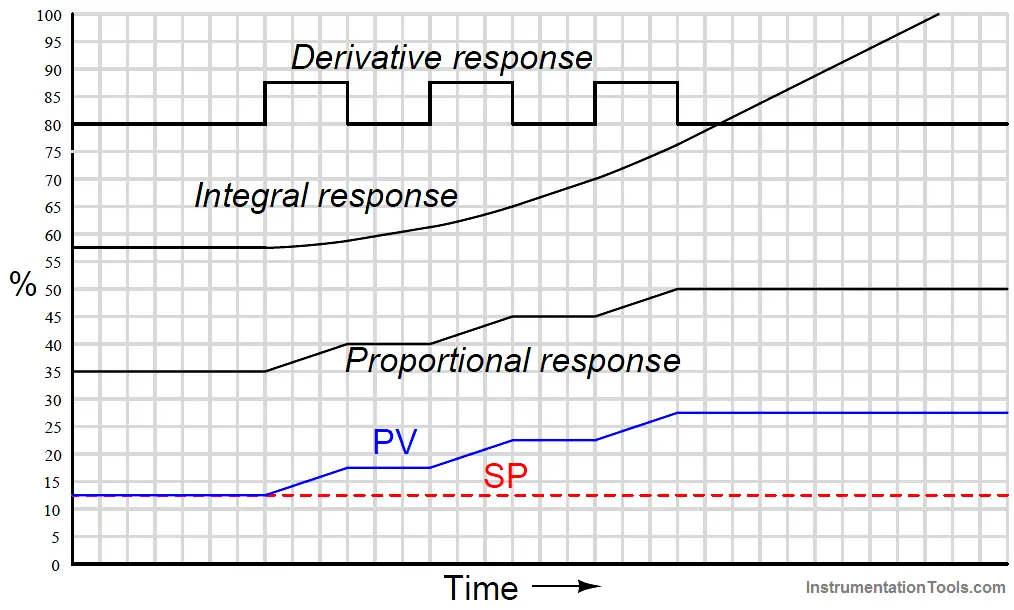
Proportional action directly mimics the ramp-and-step shape of the input. Integral action ramps slowly at first (when the error is small) but increases ramping rate as error increases.
Which each higher ramp-and-step in PV, integral action winds up at an ever-increasing rate. Since PV never equals SP again, integral action never stops ramping upward. Derivative action steps with each ramp of the PV.
When combined into one PID output, the three actions produce this response:
Responses to a sine wavelet input
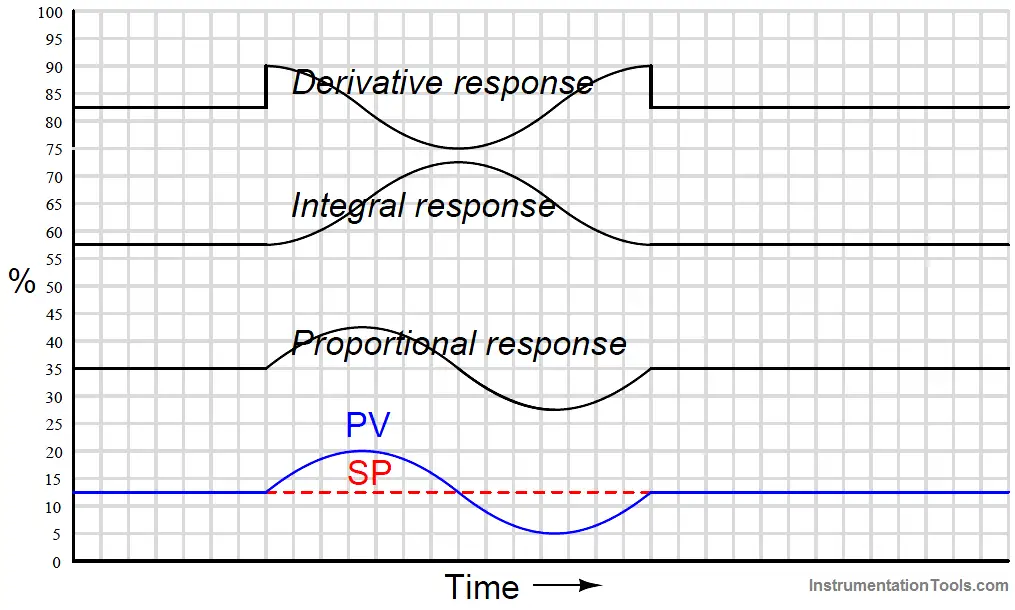
As always, proportional action directly mimics the shape of the input. The 90o phase shift seen in the integral and derivative responses, compared to the PV wavelet, is no accident or coincidence.
The derivative of a sinusoidal function is always a cosine function, which is mathematically identical to a sine function with the angle advanced by 90 o :
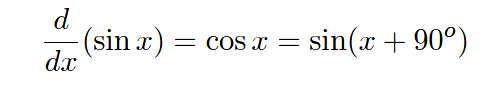
Conversely, the integral of a sine function is always a negative cosine function, which is mathematically identical to a sine function with the angle retarded by 90 o :
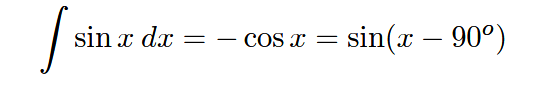
In summary, the derivative operation always adds a positive (leading) phase shift to a sinusoidal input waveform, while the integral operation always adds a negative (lagging) phase shift to a sinusoidal input waveform.
When combined into one PID output, these particular integral and derivative actions mostly cancel, since they happen to be sinusoidal wavelets of equal amplitude and opposite phase.
Thus, the only way that the final (PID) output differs from proportional-only action in this particular case is the “steps” caused by derivative action responding to the input’s sudden rise at the beginning and end of the wavelet:
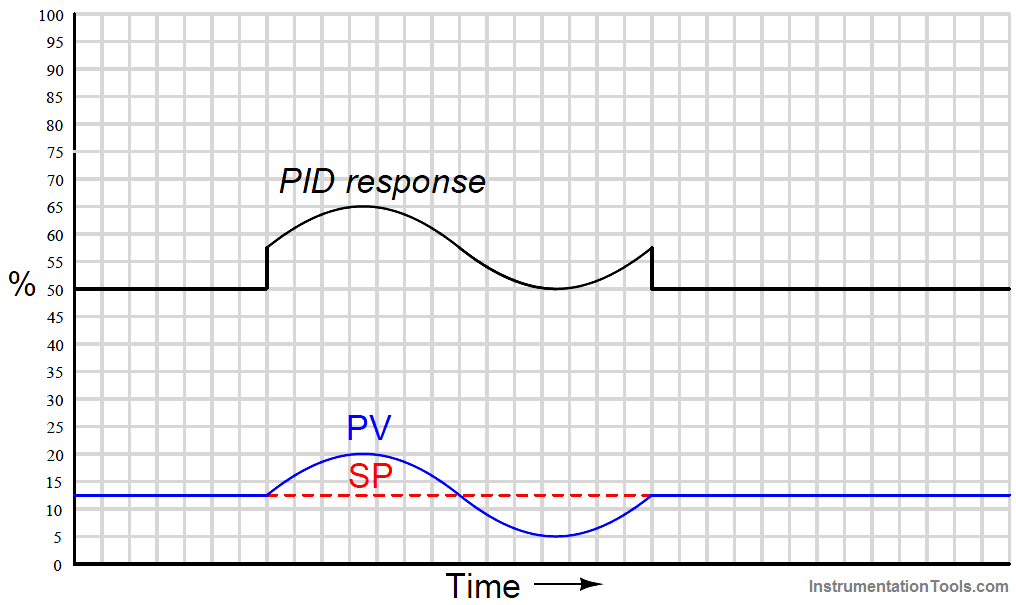
If the I and D tuning parameters were such that the integral and derivative responses were not equal in amplitude, their effects would not completely cancel.
Rather, the resultant of P, I, and D actions would be a sine wavelet having a phase shift somewhere between −90o and +90o exclusive, depending on the relative strengths of the P, I, and D actions.
The 90 degree phase shifts associated with the integral and derivative operations are useful to understand when tuning PID controllers.
If one is familiar with these phase shift relationships, it is relatively easy to analyze the response of a PID controller to a sinusoidal input (such as when a process oscillates following a sudden load or setpoint change) to determine if the controller’s response is dominated by any one of the three actions.
This may be helpful in “de-tuning” an over-tuned (overly aggressive) PID controller, if an excess of P, I, or D action may be identified from a phase comparison of PV and output waveforms.
Credits : Tony R. Kuphaldt – Creative Commons Attribution 4.0 License











Great post! Very informative.
very nicely information given. thank you