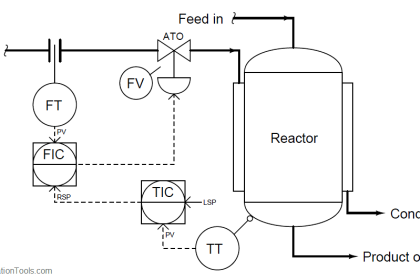
A common exercise for students learning the function of PID controllers is to practice graphing a controller’s output with given input (PV and SP) conditions, either qualitatively or quantitatively.
This can be a frustrating experience for some students, as they struggle to accurately combine the effects of P, I, and/or D responses into a single output trend. Here, I will present a way to ease the pain.
PID Controllers
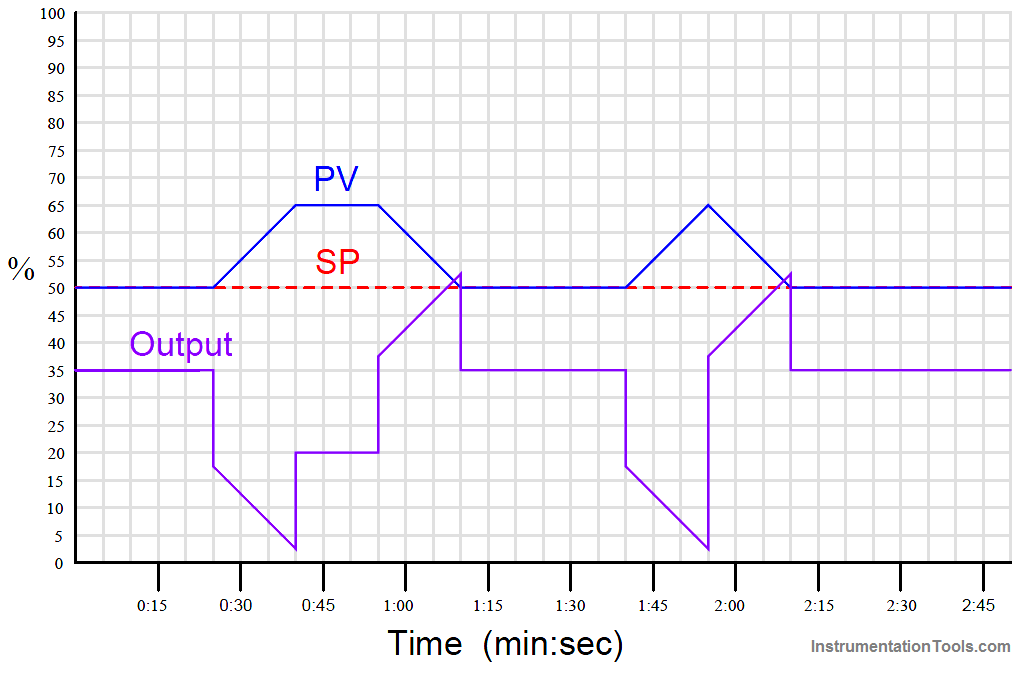
Suppose for example you were tasked with graphing the response of a PD (proportional + derivative) controller to the following PV and SP inputs over time.
You are told the controller has a gain of 1, a derivative time constant of 0.3 minutes, and is reverse-acting:
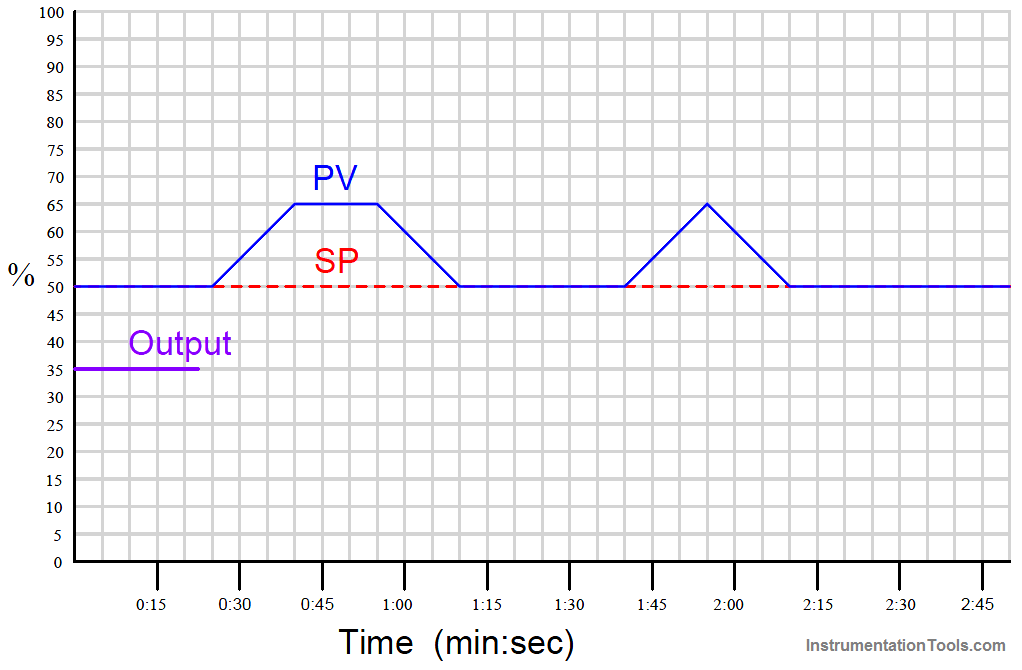
My first recommendation is to qualitatively sketch the individual P and D responses. Simply draw two different trends, each one right above or below the given PV/SP trends, showing the shapes of each response over time.
You might even find it easier to do if you re-draw the original PV and SP trends on a piece of non-graph paper with the qualitative P and D trends also sketched on the same piece of non-graph paper.
The purpose of the qualitative sketches is to separate the task of determining shapes from the task of determining numerical values, in order to simplify the process.
After sketching the separate P and D trends, label each one of the “features” (changes either up or down) in these qualitative trends. This will allow you to more easily combine the effects into one output trend later:
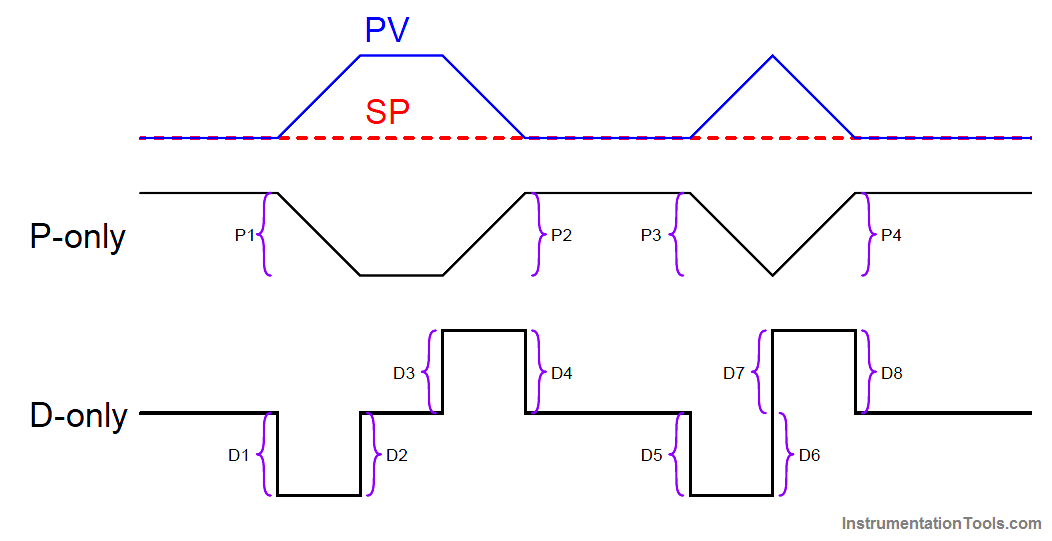
Now, you may qualitatively sketch an output trend combining each of these “features” into one graph.
Be sure to label each ramp or step originating with the separate P or D trends, so you know where each “feature” of the combined output graph originates from:
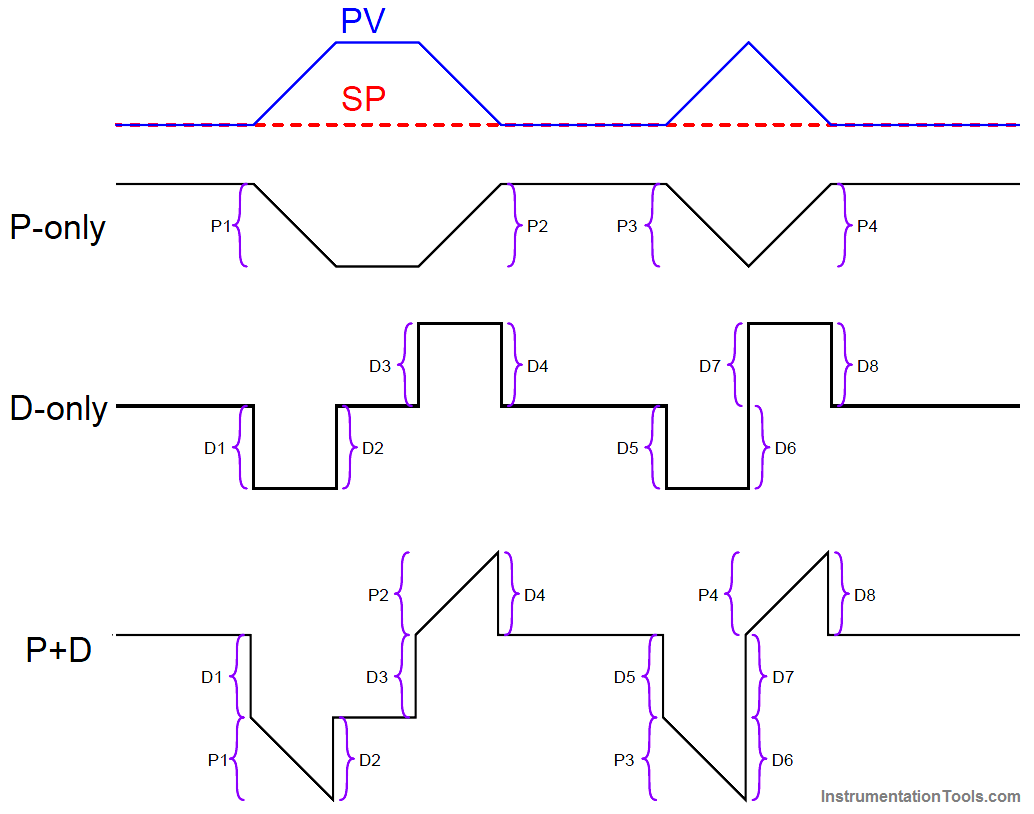
Once the general shape of the output has been qualitatively determined, you may go back to the separate P and D trends to calculate numerical values for each of the labeled “features.”
Note that each of the PV ramps is 15% in height, over a time of 15 seconds (one-quarter of a minute). With a controller gain of 1, the proportional response to each of these ramps will also be a ramp that is 15% in height.
Taking our given derivative time constant of 0.3 minutes and multiplying that by the PV’s rate-of-change ( dPV/dt ) during each of its ramping periods (15% per one-quarter minute, or 60% per minute) yields a derivative response of 18% during each of the ramping periods. Thus, each derivative response “step” will be 18% in height.
Going back to the qualitative sketches of P and D actions, and to the combined (qualitative) output sketch, we may apply the calculated values of 15% for each proportional ramp and 18% for each derivative step to the labeled “features.”
We may also label the starting value of the output trend as given in the original problem (35%), to calculate actual output values at different points in time.
Calculating output values at specific points in the graph becomes as easy as cumulatively adding and subtracting the P and D “feature” values to the starting output value:
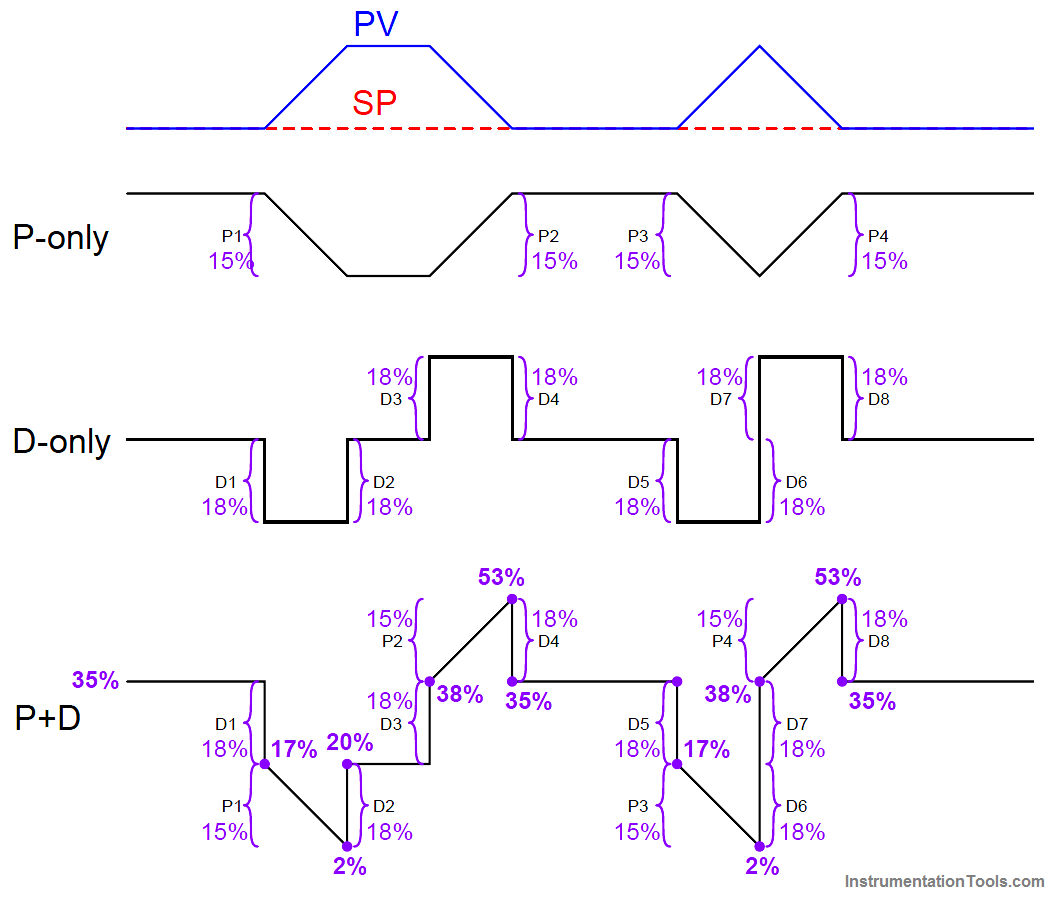
Now that we know the output values at all the critical points, we may quantitatively sketch the output trend on the original graph:
Credits : Tony R. Kuphaldt – Creative Commons Attribution 4.0 License