The final element of PID control is the “D” term, which stands for derivative. This is a calculus concept like integral, except most people consider it easier to understand. Simply put, derivative is the expression of a variable’s rate-of-change with respect to another variable.
Finding the derivative of a function (differentiation) is the inverse operation of integration. With integration, we calculated accumulated value of some variable’s product with time.
With derivative, we calculate the ratio of a variable’s change per unit of time. Whereas integration is fundamentally a multiplicative operation (products), differentiation always involves division (ratios).
A controller with derivative (or rate) action looks at how fast the process variable changes per unit of time, and takes action proportional to that rate of change. In contrast to integral (reset) action which represents the “impatience” of the controller, derivative (rate) action represents the “caution” of the controller.
If the process variable starts to change at a high rate of speed, the job of derivative action is to move the final control element in such a direction as to counteract this rapid change, and thereby moderate the speed at which the process variable changes. In simple terms, derivative action works to limit how fast the error can change.
What this will do is make the controller “cautious” with regard to rapid changes in process variable. If the process variable is headed toward the setpoint value at a rapid rate, the derivative term of the equation will diminish the output signal, thus tempering the controller’s response and slowing the process variable’s approach toward setpoint. This is analogous to a truck driver preemptively applying the brakes to slow the approach to an intersection, knowing that the heavy truck doesn’t “stop on a dime.” The heavier the truck’s load, the sooner a cautious driver will apply the brakes, to avoid “overshoot” beyond the stop sign and into the intersection. For this reason, derivative control action is also called pre-act in addition to being called rate, because it acts “ahead of time” to avoid overshoot.
If we modify the controller equation to incorporate differentiation, it will look something like this:
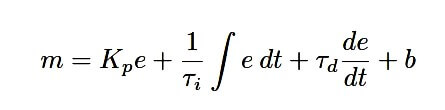
Where,
m = Controller output
e = Error (difference between PV and SP)
Kp = Proportional gain
Ti= Integral time constant (minutes)
Td = Derivative time constant (minutes)
t = Time
b = Bias
The de/dt term of the equation expresses the rate of change of error (e) over time (t). The lower-case letter “d” symbols represent the calculus concept of differentials which may be thought of in this context as very tiny increments of the following variables. In other words, de/dt refers to the ratio of a very small change in error (de) over a very small increment of time (dt). On a graph, this is interpreted as the slope of a curve at a specific point (slope being defined as rise over run).
It is also possible to build a controller with proportional and derivative actions, but lacking integral action. These are most commonly used in applications prone to wind-up , and where the elimination of offset is not critical:
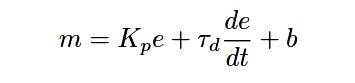
Many PID controllers offer the option of calculating derivative response based on rates of change for the process variable (PV) only, rather than the error (PV − SP or SP − PV). This avoids huge “spikes” in the output of the controller if ever a human operator makes a sudden change in setpoint . The mathematical expression for such a controller would look like this:
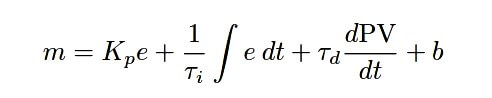
Even when derivative control action is calculated on PV alone (rather than on error), it is still useful for controlling processes dominated by large lag times. The presence of derivative control action in a PID controller generally means the proportional (P) and integral (I) terms may be adjusted more aggressively than before, since derivative (D) will act to limit overshoot. In other words, the judicious presence of derivative action in a PID controller lets us “get away” with using a bit more P and I action than we ordinarily could, resulting in faster approach to setpoint with minimal overshoot.
It should be mentioned that derivative mode should be used with caution. Since it acts on rates of change, derivative action will “go crazy” if it sees substantial noise in the PV signal. Even small amounts of noise possess extremely large rates of change (defined as percent PV change per minute of time) owing to the relatively high frequency of noise compared to the timescale of physical process changes.
The latest control effect made its appearance under the trade name “Pre-Act.” On some control applications, the addition of pre-act response made such a remarkable improvement that it appeared to be in embodiment of mythical “anticipatory” controllers. On other applications it appeared to be worse than useless. Only the difficulty of predicting the usefulness and adjustment of this response has kept it from being more widely used.










You guys are adding much value to the competency and knowledge base of many of us.
Thanks so much for this platform.