All masses require force to accelerate (we can also think of this in terms of the mass generating a reaction force as a result of being accelerated). This is quantitatively expressed by Newton’s Second Law of Motion:
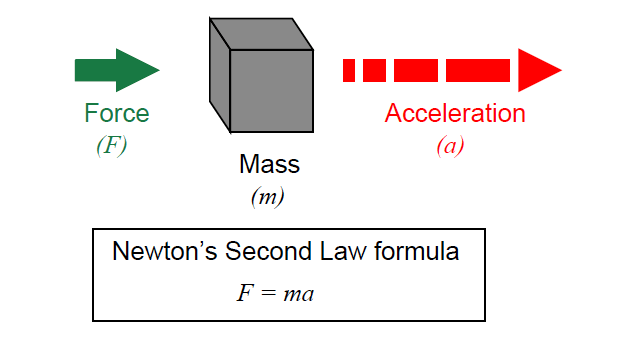
All fluids possess mass, and therefore require force to accelerate just like solid masses.
If we consider a quantity of fluid confined inside a pipe, with that fluid quantity having a mass equal to its volume multiplied by its mass density (m = ρV , where ρ is the fluid’s mass per unit volume), the force required to accelerate that fluid “plug” would be calculated just the same as for a solid mass:
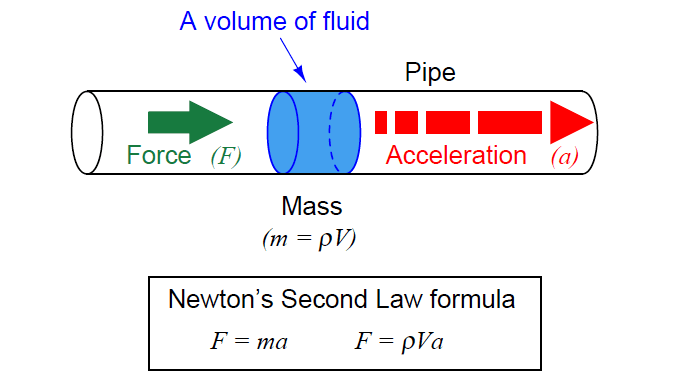
Since this accelerating force is applied on the cross-sectional area of the fluid plug, we may express it as a pressure, the definition of pressure being force per unit area:
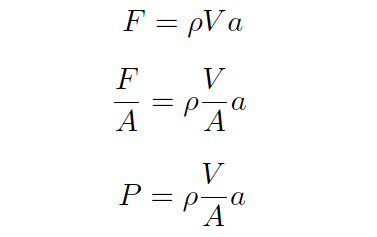
Since the rules of algebra required we divide both sides of the force equation by area, it left us with a fraction of volume over area (V/A) on the right-hand side of the equation.
This fraction has a physical meaning, since we know the volume of a cylinder divided by the area of its circular face is simply the length of that cylinder:
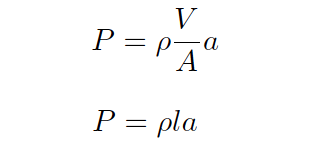
When we apply this to the illustration of the fluid mass, it makes sense: the pressure described by the equation is actually a differential 3 pressure drop from one side of the fluid mass to the other, with the length variable (l) describing the spacing between the differential pressure ports:
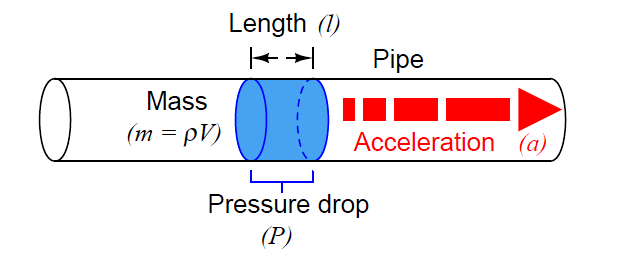
This tells us we can accelerate a “plug” of fluid by applying a difference of pressure across its length.
The amount of pressure we apply will be in direct proportion to the density of the fluid and its rate of acceleration. Conversely, we may measure a fluid’s rate of acceleration by measuring the pressure developed across a distance over which it accelerates.
We may easily force a fluid to accelerate by altering its natural flow path. The difference of pressure generated by this acceleration will indirectly indicate the rate of acceleration.
Since the acceleration we see from a change in flow path is a direct function of how fast the fluid was originally moving, the acceleration (and therefore the pressure drop) indirectly indicates fluid flow rate.
A very common way to cause linear acceleration in a moving fluid is to pass the fluid through a constriction in the pipe, thereby increasing its velocity (remember that the definition of acceleration is a change in velocity).
Pressure based Flow Meters
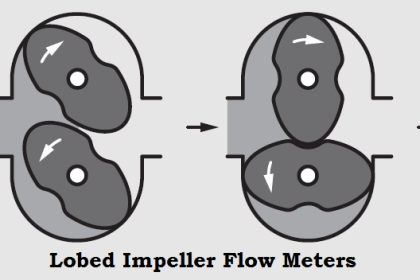
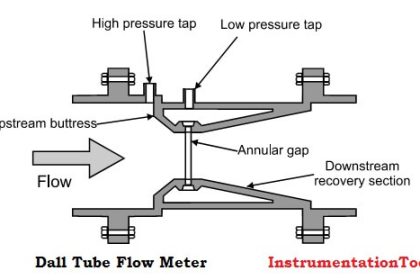
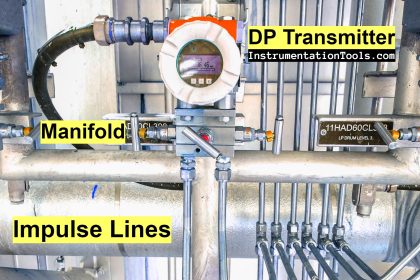
The following illustrations show several devices used to linearly accelerate moving fluids when placed in pipes, with differential pressure transmitters connected to measure the pressure drop resulting from this acceleration:
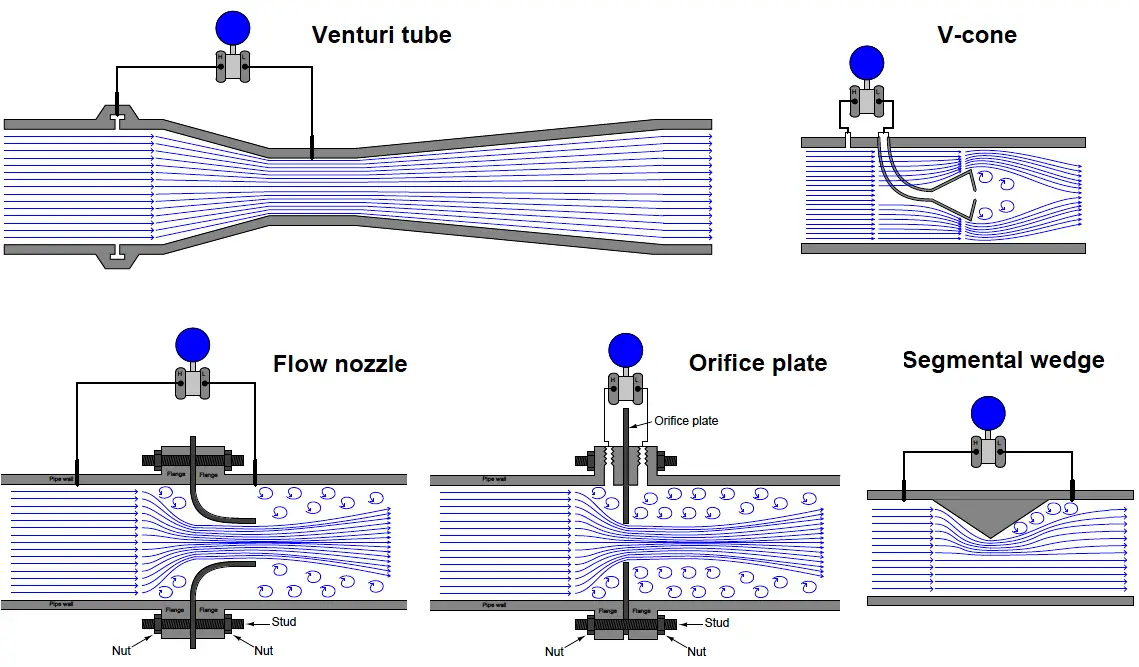
Read the detailed topics on below flow meters :
Another way we may accelerate a fluid is to force it to turn a corner through a pipe fitting called an elbow.
This will generate radial acceleration, causing a pressure difference between the outside and inside of the elbow which may be measured by a differential pressure transmitter:
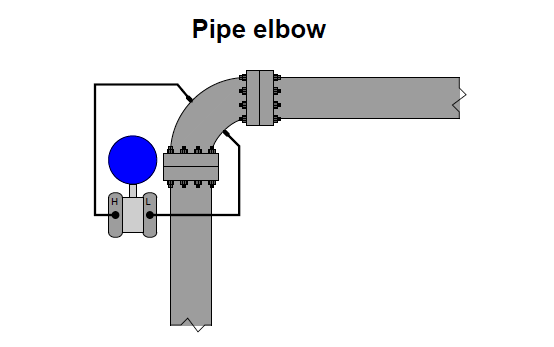
Note : we do not use this type of installation for flow measurement in real world
The pressure tap located on the outside of the elbow’s turn registers a greater pressure than the tap located on the inside of the elbow’s turn, due to the inertial force of the fluid’s mass being “flung” to the outside of the turn as it rounds the corner.
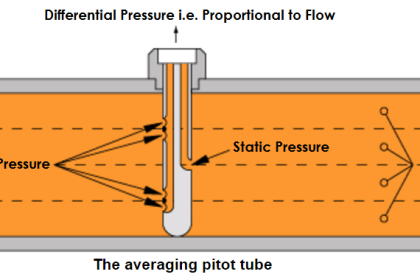
Yet another way to cause a change in fluid velocity is to force it to decelerate by bringing a portion of it to a full stop. The pressure generated by this deceleration (called the stagnation pressure) tells us how fast it was originally flowing.
A few devices working on this principle are shown here:
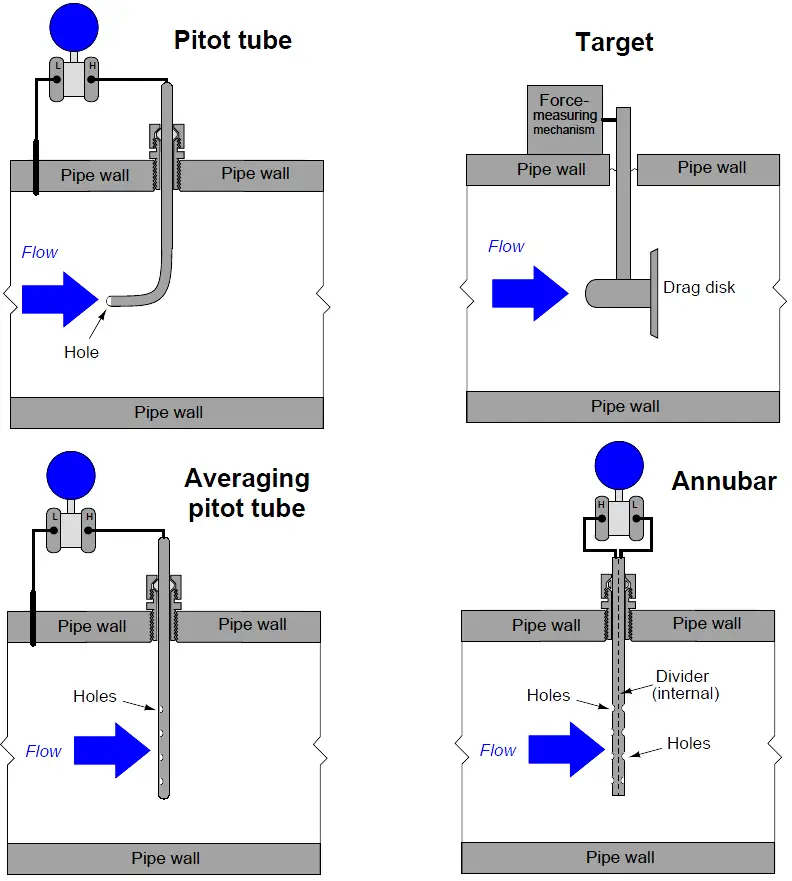
Different primary sensing elements (PSE’s) used to generate differential pressure in a moving fluid stream.
Despite their very different designs, they all operate on the same fundamental principle: causing a fluid to accelerate or decelerate by forcing a change in its flow path, and thus generating a measurable pressure difference.
Sir , Also include calibration of Circular flow recorder
Can venturi flowmeter detect reverse flow. What configuration is needed in transmitter and DCS. Please clarify