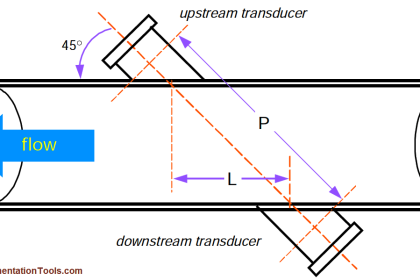
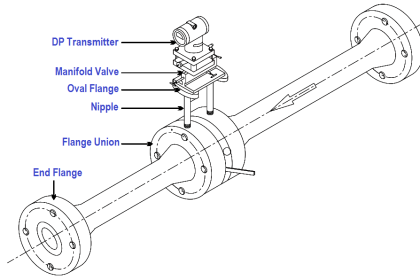
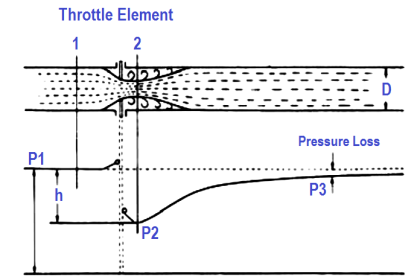
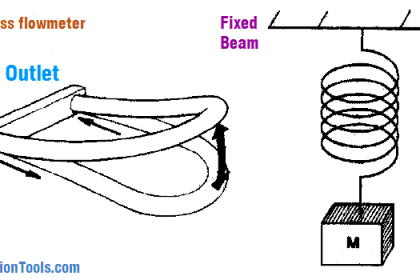
Measurements of mass flow are preferred over measurements of volumetric flow in process applications where mass balance (monitoring the rates of mass entry and exit for a process) is important.
Whereas volumetric flow measurements express the fluid flow rate in such terms as gallons per minute or cubic meters per second, mass flow measurements always express fluid flow rate in terms of actual mass units over time, such pounds (mass) per second or kilograms per minute.
Mass Flow
Applications for mass flow measurement include custody transfer (where a fluid product is bought or sold by its mass), chemical reaction processes (where the mass flow rates of reactants must be maintained in precise proportion in order for the desired chemical reactions to occur), and steam boiler control systems (where the out-flow of vaporous steam must be balanced by an equivalent in-flow of liquid water to the boiler – here, volumetric comparisons of steam and water flow would be useless because one cubic foot of steam is certainly not the same number of H2O molecules as one cubic foot of water).
If we wish to calculate mass flow instead of volumetric flow, the equation does not change much. The relationship between volume (V ) and mass (m) for a sample of fluid is its mass density (ρ):
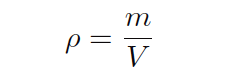
Similarly, the relationship between a volumetric flow rate (Q) and a mass flow rate (W) is also the fluid’s mass density (ρ):
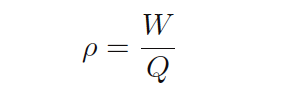
Solving for W in this equation leads us to a product of volumetric flow rate and mass density:
W = ρQ
A quick dimensional analysis check using common metric units confirms this fact. A mass flow rate in kilograms per second will be obtained by multiplying a mass density in kilograms per cubic meter by a volumetric flow rate in cubic meters per second:
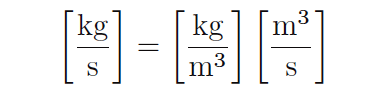
Therefore, all we have to do to turn our general volumetric flow equation into a mass flow equation is multiply both sides by fluid density (ρ):
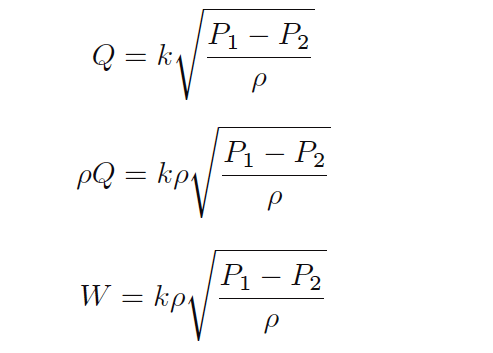
It is generally considered “inelegant” to show the same variable more than once in an equation if it is not necessary, so let’s try to consolidate the two densities (ρ) using algebra.
First, we may write ρ as the product of two square-roots:
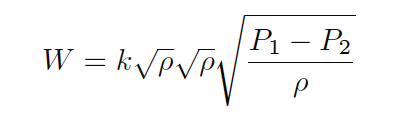
Next, we will break up the last radical into a quotient of two separate square roots:
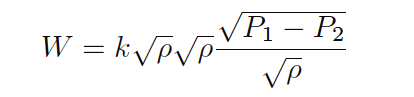
Now we see how one of the square-rooted ρ terms cancels out the one in the denominator of the fraction:
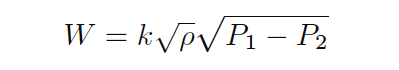
It is also considered “inelegant” to have multiple radicands in an equation where one will suffice, so we will re-write our equation for esthetic improvement:
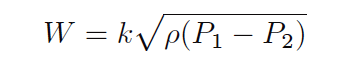
As with the volumetric flow equation, all we need in order to arrive at a suitable k value for any particular flow element is a set of values taken from that real element in service, expressed in whatever units of measurement we desire.
Also Read: Volumetric Flow Calculations
Example Calculations
if we had a venturi tube generating a differential pressure of 2.30 kilopascals (kPa) at a mass flow rate of 500 kilograms per minute of naphtha (a petroleum product having a density of 0.665 kilograms per liter), we could solve for the k value of this venturi tube as such:
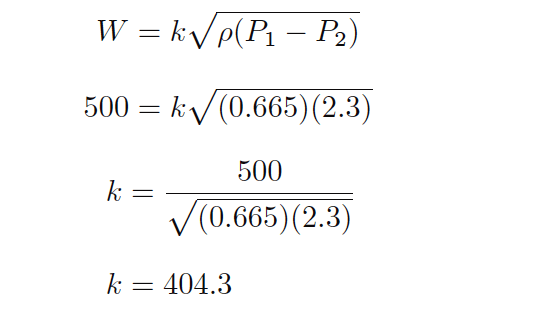
Now that we know a value of 404.3 for k will yield kilograms per minute of liquid flow through this venturi tube given pressure in kPa and density in kilograms per liter, we may readily predict the mass flow rate through this tube for any other pressure drop and fluid density we might happen to encounter.
The value of 404.3 for k relates the disparate units of measurement for us:
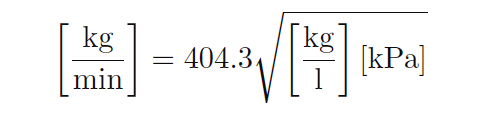
As with volumetric flow calculations, the calculated value for k neatly accounts for any set of measurement units we may arbitrarily choose. The key is first knowing the proportional relationship between flow rate, pressure drop, and density.
Once we combine that proportionality with a specific set of data experimentally gathered from a particular flow element, we have a true equation properly relating all the variables together in our chosen units of measurement.
If we happened to measure 6.1 kPa of differential pressure across this same venturi tube as it flowed sea water (density = 1.03 kilograms per liter), we could calculate the mass flow rate quite easily using the same equation (with the k factor of 404.3):
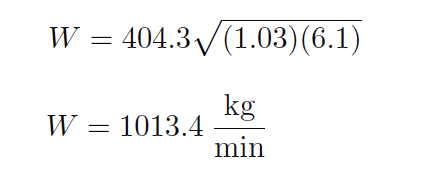
Credits: Tony R. Kuphaldt – Creative Commons Attribution 4.0 License
If you liked this article, then please subscribe to our YouTube Channel for Electrical, Electronics, Instrumentation, PLC, and SCADA video tutorials.
You can also follow us on Facebook and Twitter to receive daily updates.
Read Next:
- Flow Measurement Questions
- Pressure based Flow meters
- Introduction to Flow measurement
- Calibration of Turbine Flow Meter
- Flow meter Scaling Factor