What is Differential Pressure Flow Meter?

Differential pressure meters work on the principle of partially obstructing the flow in a pipe. This creates a difference in the static pressure between the upstream and downstream sides of the device.

This difference in the static pressure (referred to as the differential pressure) is measured and used to determine the flow rate.

What is a Differential Pressure Meter?

Differential-pressure meters are hugely popular and it is estimated that at least 40% of industrial flow meters in use at present are differential-pressure devices, with the orifice plate being the most popular. Differential-pressure devices have been used to meter a wide variety of different fluids from gases to highly viscous liquids.

The popularity of differential-pressure flow meters is in part due to their simple design and low cost. By reading this guide you will have a much clearer idea of the benefits, viable metering options, and applications for using differential-pressure meters.

Differential Pressure Flow Meter

The concept of using the pressure drop caused by a fluid flowing through a restriction in a pipe as a measurement of flow rate dates back to the 18th Century, when it was discovered by Bernoulli.

The basic principle of how a Δp flow meter operates is described in the figure below.

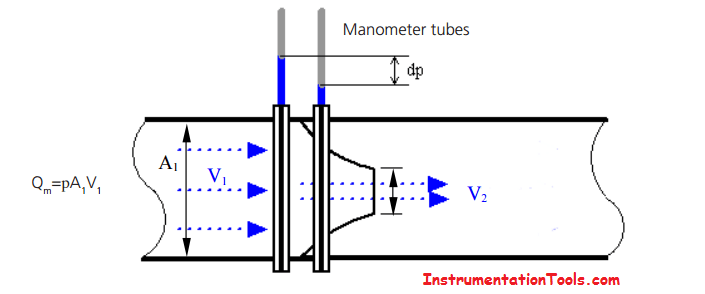
The differential pressure principle. Manometer tubes measure the difference in static pressure upstream and downstream of the restriction

When a fluid flows through a restriction, it accelerates to a higher velocity (i.e. V2 > V1 ) to conserve the mass flow, and, as a consequence of this, its static pressure drops. This differential pressure (Δp) is then a measure of the flow rate through the device.

In simple terms for a given size of restriction, the higher the Δp, the higher the flow rate.

The relationship between the differential pressure and flow rate is derived from Bernoulli’s equation.

Using Bernoulli’s equation, and conservation of mass, it can be shown that the differential pressure generated is proportional to the square of the mass flow rate, Qm (kg/s)

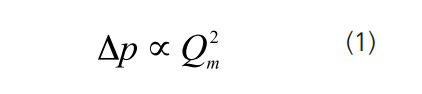
Many of the Δp meters available work on this principle of measuring the difference in pressure between upstream and downstream but there are some meters that use the differential pressure in other ways, for example, variable area meters.

Types of Differential Pressure Flow Meter

The most common types of differential pressure meter are:

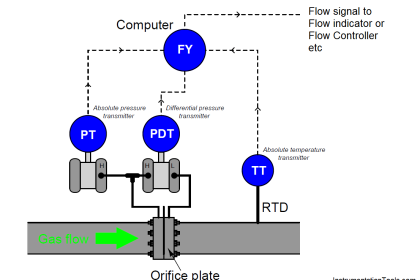
• Orifice plates
• Venturi tubes
• Cone meters (e.g. V-cones)
• Nozzles
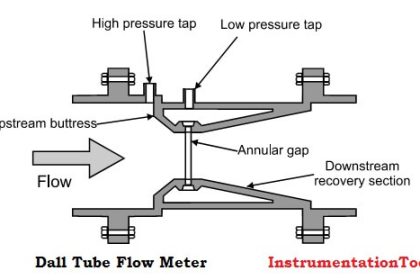
• Low-loss meters (e.g. Dall tubes)
• Variable area meters
• Inlet flow meters
• Venturi cones
• Venturi nozzles
• Drag plates

Pros and Cons of DP meters

There are a number of general advantages common to most DP meters.

These include:

• They are simple to make, containing no moving parts
• Their performance is well-understood
• They are cheap – especially in larger pipes when compared with other meters
• They can be used in any orientation
• They can be used for most gases and liquids
• Some types do not require calibration for certain applications

The main disadvantages of DP meters are:

• Rangeability (turndown) is less than for most other types of flow meter
• Significant pressure losses may occur
• The output signal is non-linear with flow
• The discharge coefficient and accuracy may be affected by pipe layout or the nature of the flow
• They may suffer from aging effects, e.g. the build-up of deposits or erosion of sharp edges

Common Terminology

Beta (β)

The diameter ratio or beta (sometimes referred to as the beta ratio) is the ratio between the diameter of the orifice or throat of the device to that of the pipe.

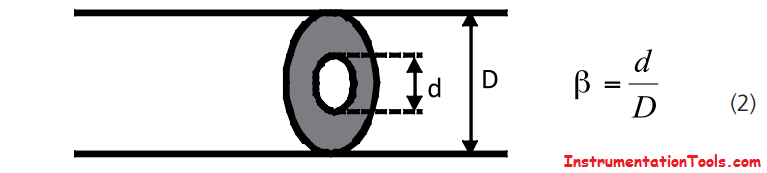
Often Δp meters are described in terms of their beta value and diameter to fit a certain pipeline size, for example, a 4-inch β= 0.6 Venturi tube.

To state that a Δp meter has a low beta ratio, for example, β = 0.2, means the plate has a small hole or restriction size.

This causes the pressure loss across the Δp meter to be higher, which may mean that a pump with a higher discharge pressure (hence more expensive) or compressor will be needed to overcome the increased pressure loss and maintain a flow rate achievable with a larger beta Δp meter.

On the other hand, a higher differential pressure can generally be measured more accurately than a lower one.

Effect of using different values of beta

The effects of using larger values of beta include:

• an increase in the discharge coefficient uncertainty
• a lower differential pressure is measured across the orifice plate (and this can be more difficult to measure)
• longer lengths of upstream straight pipe being required to ensure the velocity profile of the flow through the orifice plate is stable and symmetrical
• the flow profile of the flow through the orifice being more affected by the roughness of the pipe walls

There are a number of sizing packages for orifice plates available, which will calculate the dimensions of the plate required. The software uses empirical formulae based on actual testing. Most of the results are available for beta values of 0.3 to 0.7.

Advantages

• Low cost
• Ease of installation
• Availability of comprehensive standard (ISO 5167-2)
• No requirement for calibration – the value of C from the standard
• Availability of different designs, e.g. for viscous fluids, bi-directional flows, suspended solids

Disadvantages

• Low turndown (can be improved with dual range Δp cells)
• High-pressure loss (35 to almost 100% of measured Δp depending on beta)
• Errors due to erosion/damage to upstream edges
• Errors due to high sensitivity to upstream installation (especially large beta devices)

Discharge coefficient (C)

The discharge coefficient, C, is a parameter that takes account of non-ideal effects, for example, energy losses due to friction, when using Δp meters.

The discharge coefficient is basically the ratio of the actual to the measured mass flow rate.

The discharge coefficient can either be:

 1. determined from a standard

•   provides good flow measurement at a reasonable price
•    is especially suitable where repeatability is more important than accuracy

or

2. determined by calibration

• provides lower uncertainties on the flow measurement.

In nozzles and Venturi tubes the flow follows the boundary of the tube closely and the value of C is usually close to one.

However, for orifice plates C has a value of approximately 0.6. Values of C can be obtained from the standard (ISO 5167) for nozzles, Venturi tubes and orifice plates that are manufactured to the specified tolerances of the standard.

Turndown of a DP meter

The turndown of a meter is the ratio of the maximum to the minimum flowrate that can be accurately measured. Ideally a large a turndown ratio is desirable to measure a wide range of flowrates

Square relationship between flowrate and Δp:

• If the flowrate is 50% of the full scale, then the Δp is at 25% of the full Δp scale
• If the flowrate is 25% of the full scale, then the Δp is at 6.25% of the full Δp scale

The following graph illustrates the square relationship between the differential pressure and the flowrate.

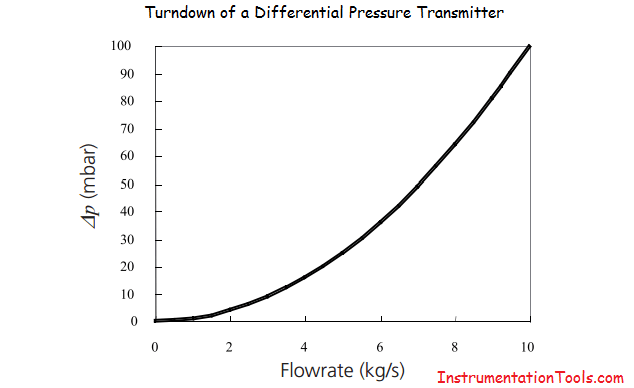
This shows that a turndown of 10:1 on flowrate will require a 100:1 turndown on pressure measurement (this is provided the density is approximately constant e.g. for a liquid).

As it is very difficult to obtain accurate measurements over such a large range of Δp values from a simple transmitter, this means that the typical turndown of a Δp meter is actually limited to approximately 4:1 to obtain an accurate measurement of flowrate.

At low values of the flowrate the Δp transmitter uncertainty increases significantly. For example, a Δp cell can typically offer an uncertainty of 0.2% of Full Scale (FS). This means that, at 1% FS, the uncertainty of the differential pressure would be 20%. Therefore at low flowrates it becomes much more difficult to measure the Δp.

The turndown of the meter can be extended to around 10:1 if multiple range transducers are used. For example, one Δp transducer could be ranged for 1 – 10% FS and another over the range of 10 – 100% FS.

Calculating the mass flow rate using DP devices

Once a value for the Δp has been obtained, the mass flow can be calculated using the following formula.

For liquids the mass flow is given by:

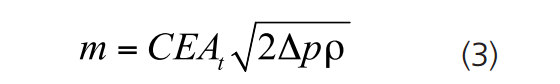
Where:

C is the discharge coefficient

At is the throat area (restriction)

Δp is the differential pressure

p is the density of the fluid

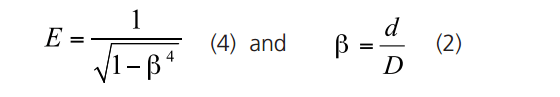
d is the diameter of the throat

D is the pipe diameter

Owing to the compressibility of gases an additional parameter called the expansibility factor, ε, is used within the mass flow equation to account for the gas density changing as the pressure drops at the restriction.

For gases the mass flow is given by:

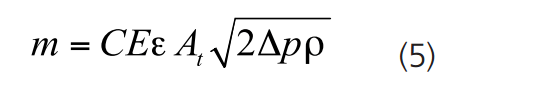
If you liked this article, then please subscribe to our YouTube Channel for Instrumentation, Electrical, PLC, and SCADA video tutorials.

You can also follow us on Facebook and Twitter to receive daily updates.

Read Next:

• Integral Flow Orifice Assembly
• What is an Orifice Flange?
• Types of Orifice Tappings
• What are the different Orifice Plates?
• Turndown ratio of Orifice Plates