When a capacitor is connected to a DC voltage source, it charges very rapidly. If no resistance was present in the charging circuit, the capacitor would become charged almost instantaneously. Resistance in a circuit will cause a delay in the time for charging a capacitor. The exact time required to charge a capacitor depends on the resistance (R) and the capacitance (C) in the charging circuit.
The below Equation illustrates this relationship.
TC = R C
where
TC = capacitive time constant (sec)
R = resistance (ohms)
C = capacitance (farad)
The capacitive time constant is the time required for the capacitor to charge to 63.2 percent of its fully charged voltage. In the following time constants, the capacitor will charge an additional 63.2 percent of the remaining voltage. The capacitor is considered fully charged after a period of five time constants (Figure 18).
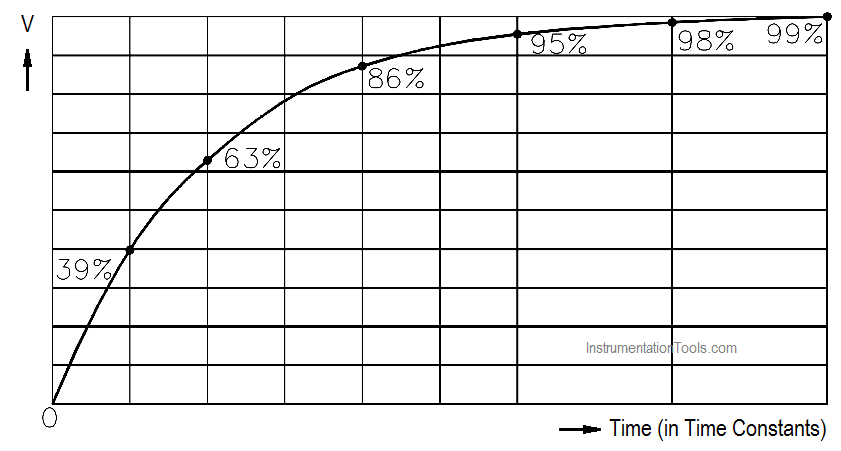
Figure 18 Capacitive Time Constant for Charging Capacitor
The capacitive time constant also shows that it requires five time constants for the voltage across a discharging capacitor to drop to its minimum value (Figure 19).
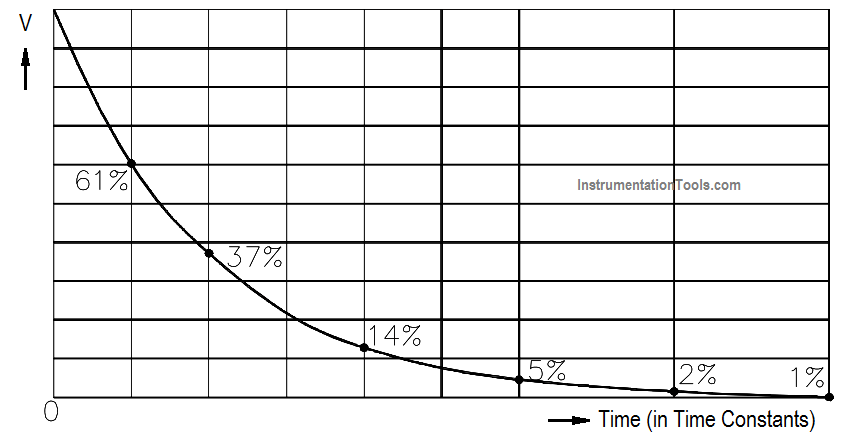
Figure 19 Capacitive Time Constant for Discharging Capacitor
Example:
Find the time constant of a 100 µF capacitor in series with a 100Ω resistor (Figure 20).
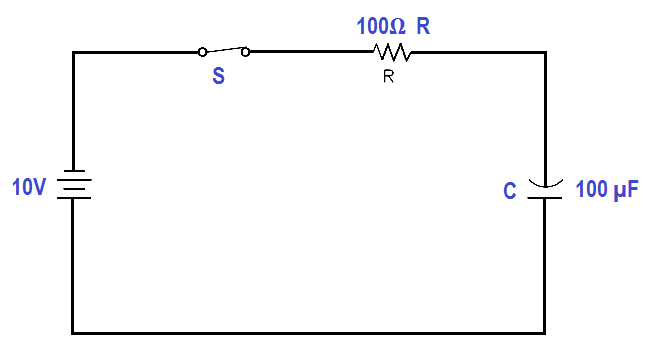
Figure 20 Example – Capacitive Time Constant
TC = R C
TC = 100 µF x 100Ω
TC = 0.01 seconds