Simplified Formulas for Parallel Circuit Resistance Calculations

Total resistance of equal resistors in a parallel circuit is equal to the resistance of one resistor divided by the number of resistors.

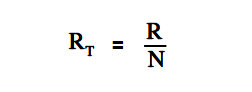
where
R_T = total resistance
R = resistance of one resistor
N = number of resistors

Example:

Five lamps, each with a resistance of 40Ω, are connected in parallel. Find total resistance.

Solution :

R1 = R2 = R3 = R4 = R5 = 40Ω

So, N = 5

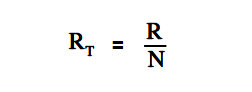
R_T = R / N = 40/5 = 8 Ω

When any two resistors are unequal in a parallel circuit, it is easier to calculate R_T by multiplying the two resistances and then dividing the product by the sum, as shown in below equation.

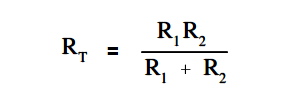
Above equation, this is valid when there are only two resistors in parallel.

Example:

Find the total resistance of a parallel circuit which has one 12Ω and one 4Ω resistor.

Solution :

• Pin

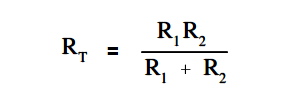
R_T = (12 x 4) / (12+4) = 48/16 = 3 Ω

In certain cases involving two resistors in parallel, it is useful to find an unknown resistor, R_x , to obtain a certain R_T. To find the appropriate formula, we start with above equation and let the known resistor be R and the unknown resistor be R_x

• Pin

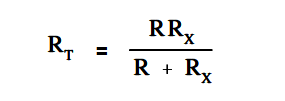
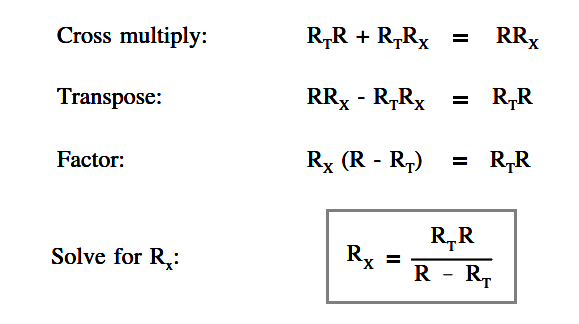
Example:

What value of resistance must be added, in parallel, with an 8Ω resistor to provide a total resistance of 6Ω (Figure 28)?

• Pin

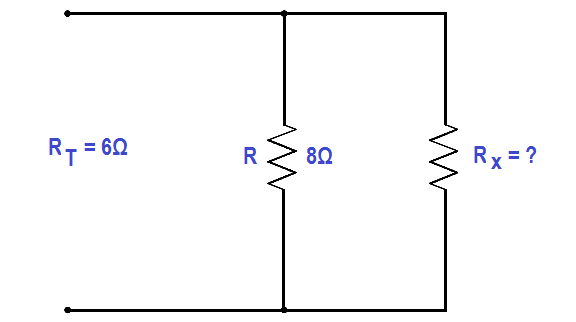
Figure 28 Example Parallel Circuit

Solution :

Rx = (R_T .R) / (R – R_T ) = (8×6)/(8+6) = 48/2 = 24 Ω