Inductance
Any device relying on magnetism or magnetic fields to operate is a form of inductor. Motors, generators, transformers, and coils are inductors. The use of an inductor in a circuit can cause current and voltage to become out-of-phase and inefficient unless corrected.
Inductive Reactance
In an inductive AC circuit, the current is continually changing and is continuously inducing an EMF. Because this EMF opposes the continuous change in the flowing current, its effect is measured in ohms. This opposition of the inductance to the flow of an alternating current is called inductive reactance (XL).
The below Equation is the mathematical representation of the current flowing in a circuit that contains only inductive reactance.
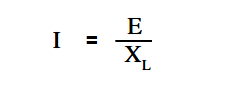
where
I = effective current (A)
XL= inductive reactance (Ω)
E = effective voltage across the reactance (V)
The value of XL in any circuit is dependent on the inductance of the circuit and on the rate at which the current is changing through the circuit. This rate of change depends on the frequency of the applied voltage.
The below Equation is the mathematical representation for XL.
XL = 2πfL
where
π = ~3.14
f = frequency (Hertz)
L = inductance (Henries)
The magnitude of an induced EMF in a circuit depends on how fast the flux that links the circuit is changing. In the case of self-induced EMF (such as in a coil), a counter EMF is induced in the coil due to a change in current and flux in the coil. This CEMF (counter EMF) opposes any change in current, and its value at any time will depend on the rate at which the current and flux are changing at that time. In a purely inductive circuit, the resistance is negligible in comparison to the inductive reactance. The voltage applied to the circuit must always be equal and opposite to the EMF of self-induction.