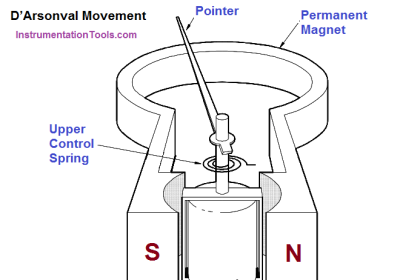
The ammeter measures electric current. It may be calibrated in amperes, milliamperes, or microamperes. In order to measure current, the ammeter must be placed in series with the circuit to be tested (as shown in below Figure 1).

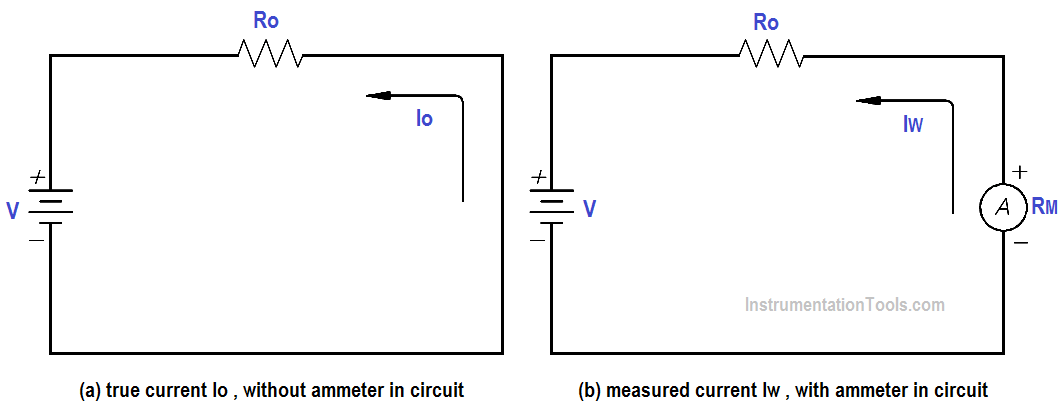
Figure 1 : Ammeter

When an ammeter is placed in series with a circuit, it will increase the resistance of that circuit by an amount equal to the internal resistance of the meter R_m.

The below Equation is the mathematical representation of the current without the meter installed.

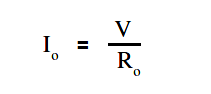
The below Equation is the mathematical representation of the current with the meter installed in the circuit.

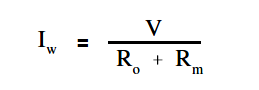
The accuracy of the ammeter K_A is the ratio of the current when the meter is in the circuit, I_w , to the current with the meter out of the circuit, I_o .

The below Equation is the mathematical representation for solving for the accuracy of the ammeter (K_A).

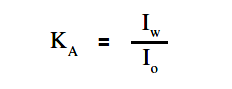
By substitution laws, The below Equation is a mathematical representation of the accuracy using circuit resistance.

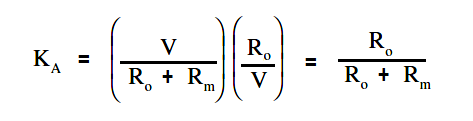
The percent loading error is that percent of error due to loading effects that result from the added resistance of the meter.

The below Equation is a mathematical representation of the percent loading error.

% loading error = (1 – K_A )(100 %)

A second error which occurs in an ammeter is calibration error. Calibration error is an error that occurs due to inaccurately marked meter faces. Typical values of calibration error in terms of full scale current are about 3 percent.

Example:

An ammeter, with a 10 mA full scale deflection and an internal resistance of 400 Ω, is placed in a circuit with a 20 V power source and a 2KΩ resistor.

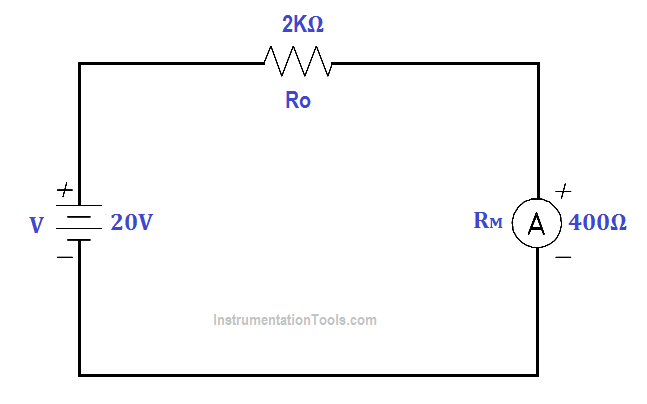
Figure 2 : Ammeter Accuracy

Find:

1. accuracy
2. %loading error
3. true current
4. measured current

Calculate Accuracy

K_A = R / (Ro + Rm)

K_A = 2000/(2000 + 2000)

K_A = 0.833 or 83.3%

Calculate %loading error

% loading error = (1 – K_A )(100 %)

% loading error = (1 – 0.833) (100%)

% loading error = 16.7 %

Calculate true current

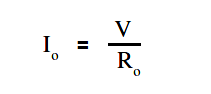
Io = 20 / 2000

Io = 0.01 A or 10mA

Calculate measured current

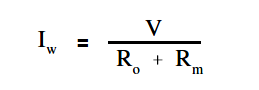
Iw = 20 / (2000 + 400)

Iw = 8.33 mA

An ammeter with a full scale I_m can be shunted with a resistor R_SH in order to measure currents in excess of I_m (as shown in Figure). The reason for shunting an ammeter is to extend the range of the ammeter and, thereby, measure currents higher than the original full scale value.

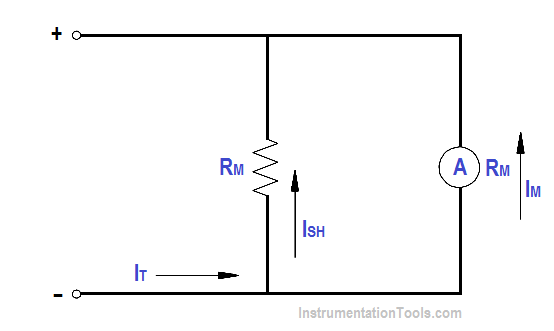
Figure 3 : Ammeter with Shunt

By Kirchhoff’s current law,

I_SH = I_T – I_m

Since the voltage across the shunt must be equal to the voltage across the ammeter, shunt resistance is calculated as follows:

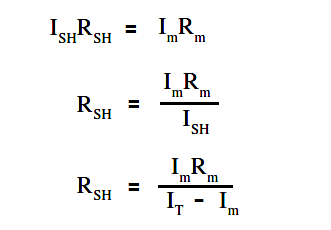
Therefore, the input resistance of a shunted ammeter is related to the meter and shunt resistance. The below Equation is a mathematical representation of this relationship.

NOTE: When computing accuracy for a shunted ammeter, use R_m‘ in place of R_m

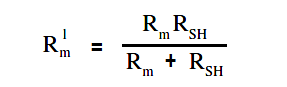
The below Equation is a mathematical representation of the relationship between input voltage and current to the ammeter and the value of input resistance.

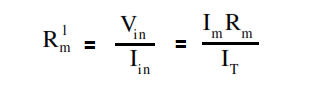
Example:

An ammeter, with a 100 Ω meter resistance and a full scale deflection current of 4 mA, is to be shunted to measure currents from 1 to 20 mA.

Find:

1. R_SH
2. R_m‘

Solution :

R_SH = (I_m R_m ) / ( I_m – R_m )

R_SH = 4 x 100 / (20-4)

R_SH = 25Ω

R_m‘ = (I_m R_m ) /  I_T

R_m‘ = 4×100 / 20

R_m‘ = 20Ω