We may measure the electrical conductivity of a liquid solution by passing an electric current through it. The most primitive form of conductivity sensor (sometimes referred to as a conductivity cell ) consists of two metal electrodes inserted in the solution, connected to a circuit designed to measure conductance (G), the reciprocal of resistance ( 1/R):

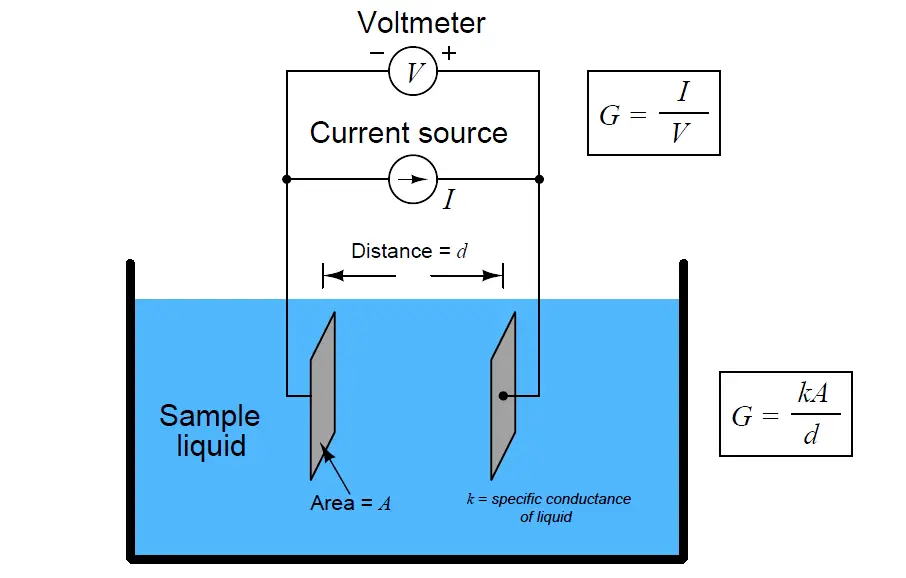
A general problem faced with electrical measurements of liquid conductance is that the derived conductance value (G) does not tell us much about the liquid itself, because that measurement depends just as much on the geometry of the plates (their area A and separation distance d) as it does on the ionic activity of the liquid solution. If we are trying to analyze the liquid all by itself, what we really need is a measurement of specific conductivity (k, or conductance) independent of plate geometry.

We face the same essential problem when trying to quantify the resistivity of metal conductors. If we measure the resistance of a piece of wire in the same manner shown in the previous illustration measuring liquid conductance, we arrive at a result that is every bit as much dependent on the length and area of the wire specimen as it is on the resistivity of the metal itself:

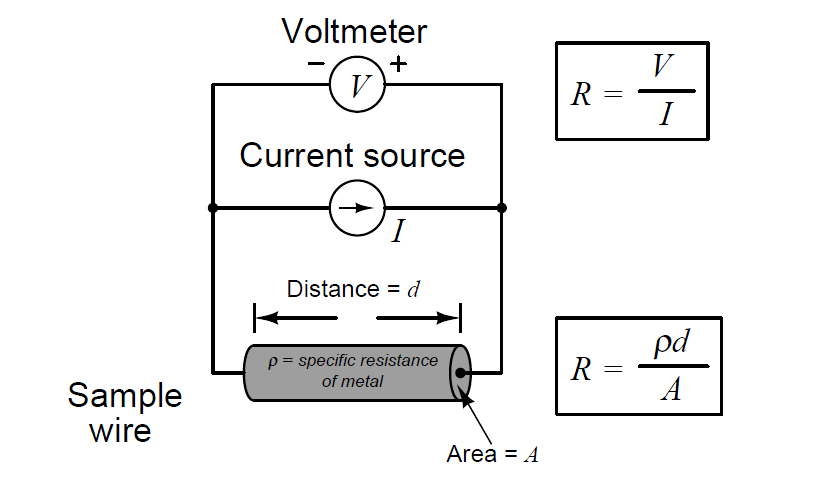
In other words, the calculated value in ohms (from direct voltage and current measurements) for the resistance of this metal specimen doesn’t tell us much about that type of metal in general, but rather it tells us the resistance of that particular specimen of wire. In order to calculate the specific resistance (ρ, or resistivity) of the metal, we must also account for the specimen’s length (d) and cross-sectional area (A).

The mathematical relationship between conductance (G), plate area (A), plate distance (d), and the actual conductivity of the liquid (k) is expressed in the following formula:

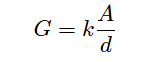
Where,
G = Conductance, in Siemens (S)
k = Specific conductance (conductivity) of liquid, in Siemens per centimeter (S/cm)
A = Electrode area (each), in square centimeters (cm2)
d = Electrode separation distance, in centimeters (cm)

Manipulating this formula to solve for conductivity (k) of the liquid:

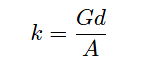
The unit of Siemens per centimeter for liquid conductivity may seem odd at first, but it is necessary to account for all the units present in the variables of the equation. A simple dimensional analysis proves this:

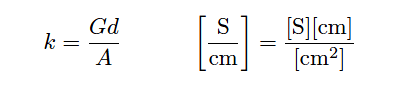
In order to quantity the plate geometry for any particular cell, manufacturers typically express the fraction d/A as a single value called the cell constant, symbolized by the Greek letter “theta” (θ) and expressed in the unit of inverse centimeters (cm⁻¹):

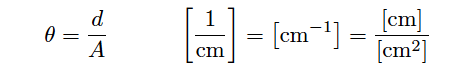
Substituting θ for the quotient d/A in the conductivity formula reveals conductivity to be the simple product of measured conductance (G) and the cell constant:

k = Gθ

Where,
k = Specific conductivity of liquid, in Siemens per centimeter (S/cm)
G = Conductance, in Siemens (S)
θ = Cell constant, in inverse centimeters (cm⁻¹)

The following photograph shows an example of such a direct-contact style of conductivity probe, consisting of stainless steel electrodes contacting the fluid flowing through a glass tube:

Two-electrode conductivity cells are not very practical in real applications, because mineral and metal ions attracted to the electrodes tend to “foul” the electrodes over time forming solid, insulating barriers on the electrodes. While this “electroplating” action may be substantially reduced by using AC instead of DC to excite the sensing circuit, it is usually not enough. Over time, the conductive barriers formed by ions bonded to the electrode surfaces will create calibration errors by making the instrument “think” the liquid is less conductive than it actually is.

Also Read : Toroidal Conductivity Sensors Principle