Transformer Voltage Ratio

The voltage of the windings in a transformer is directly proportional to the number of turns on the coils. This relationship is expressed in below Equation.

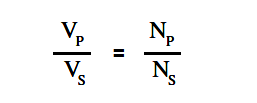
where

V_P = voltage on primary coil

V_S = voltage on secondary coil

N_P = number of turns on the primary coil

N_S = number of turns on the secondary coil

The ratio of primary voltage to secondary voltage is known as the voltage ratio (VR). As mentioned previously, the ratio of primary turns of wire to secondary turns of wire is known as the turns ratio (TR). By substituting into the above Equation, we find that the voltage ratio is equal to the turns ratio.

VR  =  TR

A voltage ratio of 1:5 means that for each volt on the primary, there will be 5 volts on the secondary. If the secondary voltage of a transformer is greater than the primary voltage, the transformer is referred to as a “step-up” transformer. A ratio of 5:1 means that for every 5 volts on the primary, there will only be 1 volt on the secondary. When secondary voltage is less than primary voltage, the transformer is referred to as a “step-down” transformer.

Example 1:

A transformer reduces voltage from 120 volts in the primary to 6 volts in the secondary. If the primary winding has 300 turns and the secondary has 15 turns, find the voltage and turns ratio.

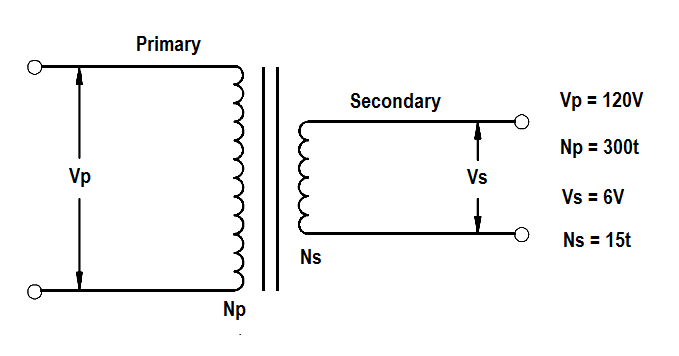
Solution:

VR = V_p/V_s

VR = 120/60

VR =  20 : 1

TR = N_p/N_s

TR = 300/15

TR =  20 : 1

Example 2:

An iron core transformer with a primary voltage of 240 volts has 250 turns in the primary and 50 turns in the secondary. Find the secondary voltage.

Solution:

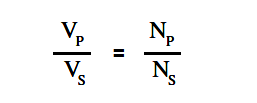
Solve for V_s

V_s  = (Ns/Np) Vp

V_s  = (50/250) 240

V_s  = 48 volts

Example 3:

A power transformer has a turns ratio of 1:4. If the secondary coil has 5000 turns and secondary voltage is 60 volts, find the voltage ratio, V_P , and N_P.

Solution:

VR = TR

VR = 1 : 4

V_P / V_S = VR = 1 : 4 = 1/4

V_P = (1/4) V_S

V_P = 60/4

V_P = 15 volts

TR = N_P / N_S

TR = 1 / 4

N_P = (1/4) N_S

N_P = 5000/4

N_P = 1250 turns