Kirchhoff’s second law is called his current law and states: “At any junction point in a circuit, the current arriving is equal to the current leaving.” Thus, if 15 amperes of current arrives at a junction that has two paths leading away from it, 15 amperes will divide among the two branches, but a total of 15 amperes must leave the junction.
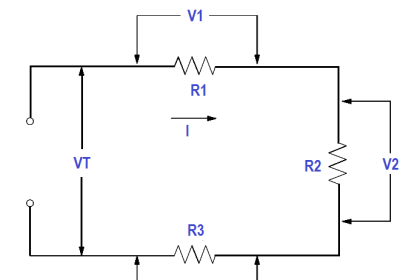
We are already familiar with Kirchhoff’s current law from parallel circuits, that is, the sum of the branch currents is equal to the total current entering the branches, as well as the total current leaving the branches (Figure 35).
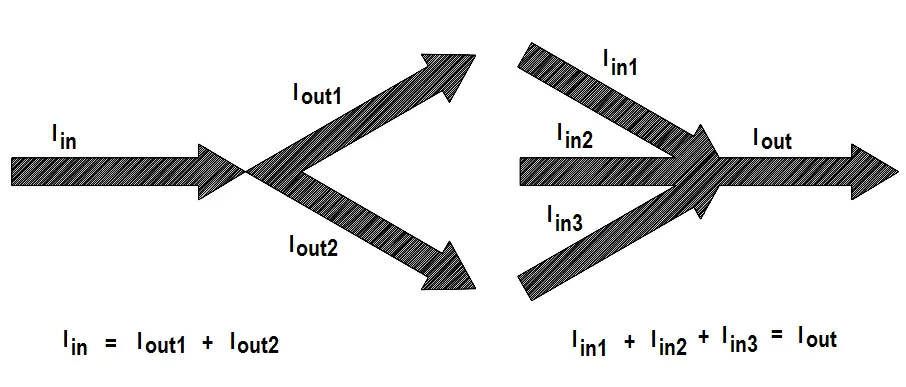
Figure 35 Illustration of Kirchhoff’s Current Law
In equation form, Kirchhoff’s current law may be expressed:
Iin – Iout = 0
Iin = Iout
Normally Kirchhoff’s current law is not used by itself, but with the voltage law, in solving a problem.
Example:
Find I2 in the circuit shown in Figure 36 using Kirchhoff’s voltage and current laws.
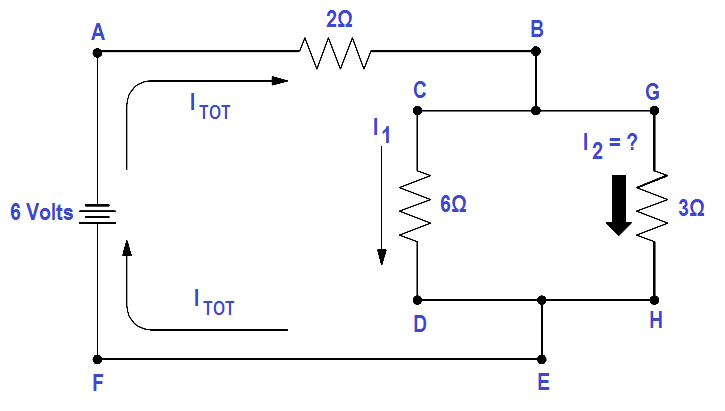Figure 36 Using the Current Law
Solution:
First, apply Kirchhoff’s voltage law to both loops.
Loop ABCDEF
∑ IR = ∑ E source
2 Itotal + 6I1 = 6
Loop ABGHEF
∑ IR = ∑ E source
2 Itotal + 3I2 = 6
Since Kirchhoff’a current law states Itotal =I1 +I2 , substitute (I1 +I2 ) in the place of Itotal in both loop equations and simplify.
Loop ABCDEF
2 (I1+ I2) +6 I1 = 6
2 I1+2 I2+6 I1= 6
8I1 +2I2= 6
Loop ABGHEF
2 (I1+ I2) +3 I2 = 6
2 I1+2 I2+3I2= 6
2I1 +5I2= 6
We now have two equations and two unknowns and must eliminate I1 to find I2 .
One way is to multiply Loop ABGHEF equation by four, and subtract Loop ABCDEF equation from the result.
Multiply by 4:
4 (2I1 +5I2 = 6 )
8I1 +20I2 + 24
Subtract :
8I1 +20I2 = 24
-(8I1 +2I2 = 6)
——————-
18I2 = 18
——————-
Now we have an equation with only I2 , which is the current we are looking for.
18I2 = 18
I2 = 18/18 = 1 amp
This circuit could have been solved simply by using Ohm’s Law, but we used Kirchhoff’s Laws to show the techniques used in solving complex circuits when Ohm’s Law cannot be used.
