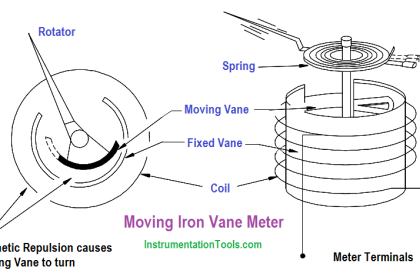
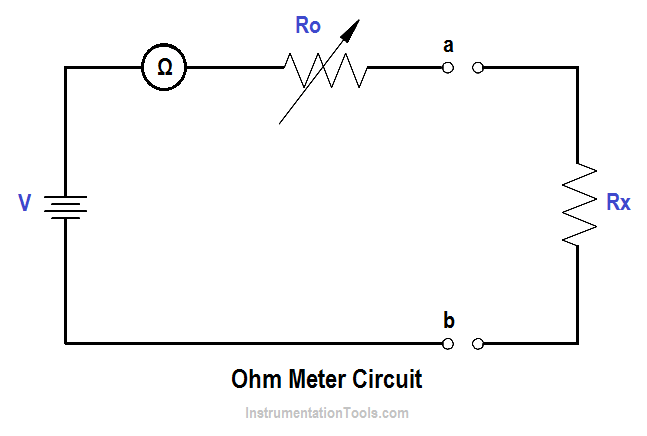
The ohm meter is an instrument used to determine resistance. A simple ohm meter (Below Figure) consists of a battery, a meter movement calibrated in ohms, and a variable resistor.
Ohm meters are connected to a component which is removed from the circuit as illustrated in Figure. The reason for removing the component is that measurement of current through the component determines the resistance. If the component remains in the circuit, and a parallel path exists in the circuit, the current will flow in the path of least resistance and give an erroneous reading.
Ro in above Figure, is an adjustable resistor whose purpose is to zero the ohm meter and correct for battery aging. It is also a current-limiting resistor which includes the meter resistance Rm. Zeroing the ohm meter is accomplished by shorting the ohm meter terminals ab and adjusting Ro to give full-scale deflection.
The below Equation is the mathematical representation for determining full-scale deflection meter current.
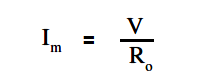
When the unknown resistance Rx is connected across the ohm meter terminals, the current is measured by calculating the total series resistance and applying above Equation.
The below Equation is the mathematical representation of this concept.
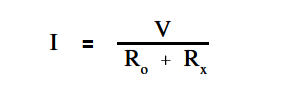
An easy way to determine ohm meter deflection is by use of a deflection factor (D). Deflection factor is the ratio of circuit current to meter current.
The below Equation is the mathematical representation of the deflection factor.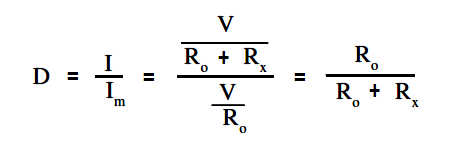
The current through the circuit can be determined by solving for I.
The below Equation is the mathematical representation of this relationship.
I = D Im
To solve for Rx , using above Equation and ” Im” equation, the relationship between deflection factor and the meter resistance to the unknown resistance can be shown. The below Equation is the mathematical representation of this relationship.
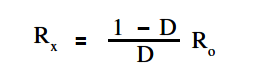
If half-scale deflection occurs, then R = Ro , so that the value of Rm is marked at mid-scale on the ohm meter face.
Example 1:
An ohm meter has a meter movement with a 100 µA full-scale deflection. The open circuit voltage at terminals ab is 24 V. The ohm meter is zeroed and then an unknown resistance Rx is measured, which produces quarter-scale deflection. Find Rx
Solution:
First find Ro
Ro = V/Im
Ro = 24/(1 x 10-6)
Ro = 240 KΩ
Then solve for Rx :
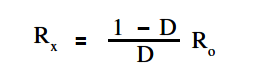
Rx = { ( 1 – 1/4) / (1/4) } 240
Rx = 720 KΩ
Therefore, quarter scale deflection of this ohm meter face would read 720 KΩ.
Example 2:
An ohm meter with Ro =30Ω, and full scale current Im = 300 µA.
Find I with: 1) 0 Ω, 2) 5Ω, 3) 10Ω, 4) 15Ω, and 5) 1 MΩ resistors across the meter terminal.
Solution:
First, the deflection factor for each resistor must be found.
D = Ro / ( Ro + Rx )
For Rx = 0 Ω
D = 30/30 = 1
For Rx = 5 Ω
D = 30/(30+5) = 0.86
For Rx = 10 Ω
D = 30/(30+10) = 0.75
For Rx = 15 Ω
D = 30/(30+15) = 0.67
For Rx = 1 M Ω
D = 30/(30+5M) = 1 x 10-6
Then find I by using:
I = D Im
For Rx = 0 Ω
I = 1 ( 300 x 10-6 ) = 300 μA (full scale deflection)
For Rx = 5 Ω
I = 0.86 ( 300 x 10-6 ) = 258 μA
For Rx = 10 Ω
I = 0.75 ( 300 x 10-6 ) = 225 μA
For Rx = 15 Ω
I = 0.67 ( 300 x 10-6 ) = 201 μA
For Rx = 1 M Ω
I = 0 ( 300 x 10-6 ) = 0 μA (zero deflection)
NOTE: As the resistance was increased from 0 to 5Ω, meter current decreased by 42 µA. Similarly, when resistance was increased from 5 to 10Ω, the current decreased by 33 µA. Thus, an ammeter scale used to measure resistance is nonlinear (below Figure).
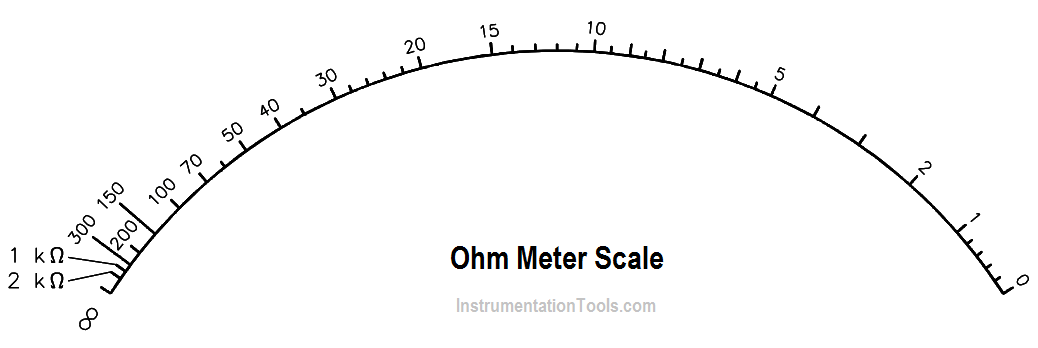
The ohm meter scale is a reversal of the ammeter and voltmeter scales. In other words, the zero resistance (Rx = 0) is at the right end of the scale and infinite resistance (Rx = 1MΩ) is at the left end of the scale.