When solving for voltage, current, and resistance in a series-parallel circuit, follow the rules which apply to the series part of the circuit, and follow the rules which apply to the parallel part of the circuit.
Solving these circuits can be simplified by reducing the circuit to a single equivalent resistance circuit, and redrawing the circuit in simplified form. The circuit is then called an equivalent circuit (Figure 46).
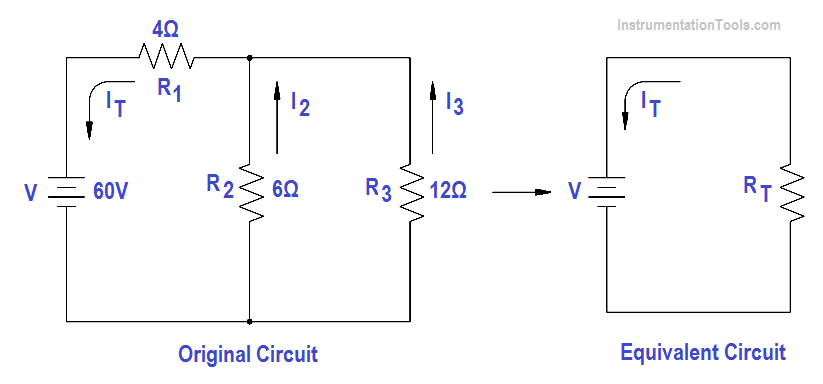
Figure 46 Redrawn Circuit Example
The easiest way to solve these types of circuits is to do it in steps.
Step 1: Find the equivalent resistance of the parallel branch:
Rp = (R2 R3 )/(R2+R3)
Rp = (6×12)/(6+12)
Rp = 72/18 = 4Ω
Step 2: Find the resistance of the equivalent series circuit:
RT = R1 +Rp = 4 + 4 = 8Ω
Step 3: Find total current (IT)
IT = V / RT = 60/8 = 7.5 amps
Step 4: Find I2 and I3 . The voltage across R1 and R2 is equal to the applied voltage (V), minus the voltage drop across R1.
V2 = V3 = V – IT R1 = 60 – (7.5 x 4) = 30V
Then, I2 and I3 are calculated.
I2 = V2/R2 = 30/6 = 5 amps
I3 = V3/R3 = 30/12 = 2.5 amps