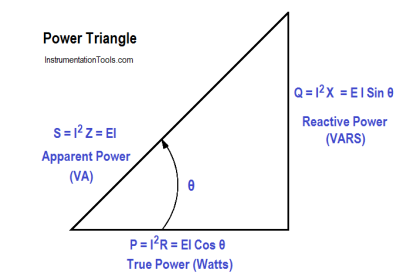
Impedance in an R-C-L series circuit is equal to the phasor sum of resistance, inductive reactance, and capacitive reactance (Figure 8).
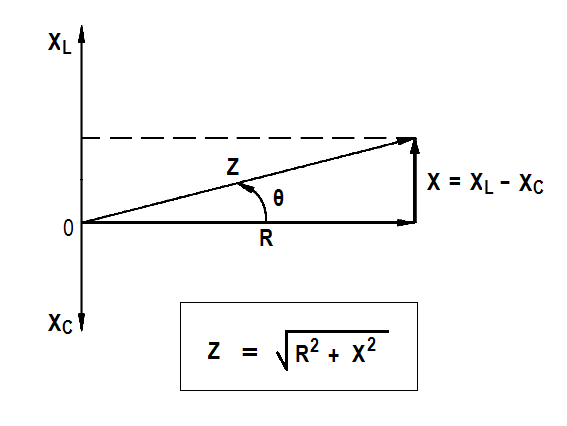
Figure 8 : Series R-C-L Impedance-Phasor
The below Equations are the mathematical representations of impedance in an R-C-L circuit. Because the difference between XL and XC is squared, the order in which the quantities are subtracted does not affect the answer.
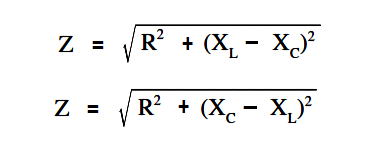
Example:
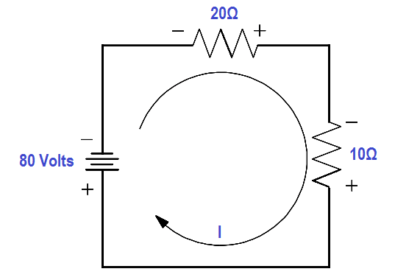
Find the impedance of a series R-C-L circuit, when R=6Ω, XL = 20Ω and XC = 10Ω (Figure 9).
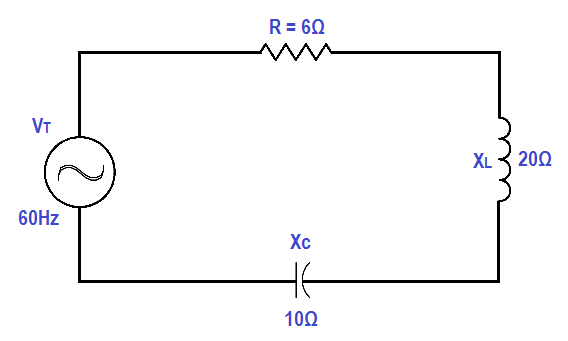
Figure 9 : Simple R-C-L Circuit
Solution:
Z = √ { R2 + (XL – XC)2 }
Z = √ { 62 + (20 – 10)2 }
Z = √136
Z = 11.66 Ω
Impedance in a parallel R-C-L circuit equals the voltage divided by the total current.
The below Equation is the mathematical representation of the impedance in a parallel R-C-L circuit.
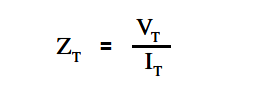
where
ZT = total impedance (Ω)
VT = total voltage (V)
IT = total current (A)
Total current in a parallel R-C-L circuit is equal to the square root of the sum of the squares of the current flows through the resistance, inductive reactance, and capacitive reactance branches of the circuit.
The below Equations are the mathematical representations of total current in a parallel R-C-L circuit. Because the difference between IL and IC is squared, the order in which the quantities are subtracted does not affect the answer.
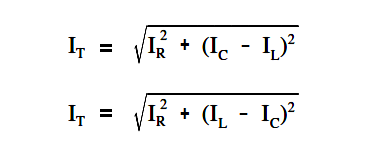
where IC>IL, first equation applies and when where IL >IC, the second equation applies.
where
IT = total current (A)
IR = current through resistance leg of circuit (A)
IC = current through capacitive reactance leg of circuit (A)
IL = current through inductive reactance leg of circuit (A)
Example:
A 200 Ω resistor, a 100 Ω XL , and an 80 Ω XC are placed in parallel across a 120V AC source (Figure 10). Find: (1) the branch currents, (2) the total current, and (3) the impedance.
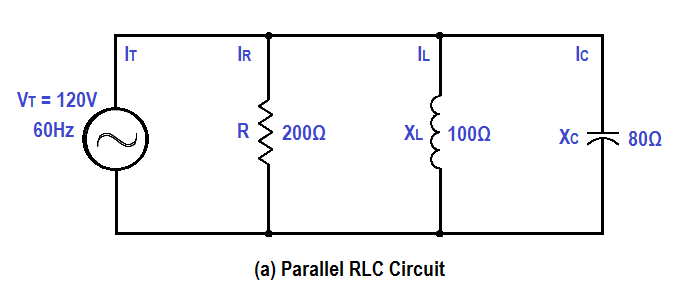
Figure 10 : Simple Parallel R-C-L Circuit
Solution:
1. Branch currents
IR = VT/R = 120/200 = 0.6A
IL = VT/XL = 120/100 = 1.2A
IC = VT/XC = 120/80 = 1.5A
2. Total current
IT = √ { IR2+ (IC – IL)2 }
IT = √ { 0.62+ (1.5 – 1.2)2 }
IT = √ { 0.36 + 0.09 }
IT = √0.45 = 0.671 A
3. Impedance
Z = VT / IT
Z = 120 / 0.671
Z = 178.8 Ω