Reliability, as previously defined, is the probability a component or system will perform as designed. Like all probability values, reliability is expressed a number ranging between 0 and 1, inclusive.
A reliability value of zero (0) means the component or system is totally unreliable (i.e. it is guaranteed to fail). Conversely, a reliability value of one (1) means the component or system is completely reliable (i.e. guaranteed to properly function).
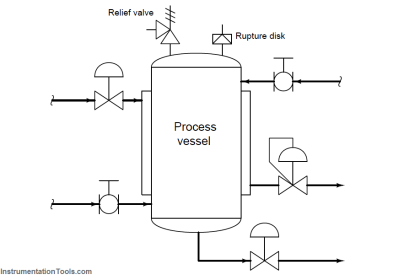
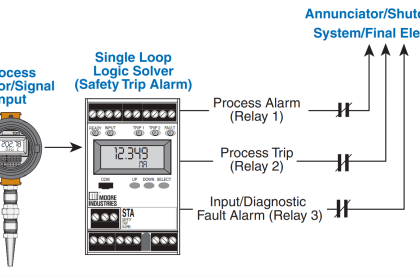
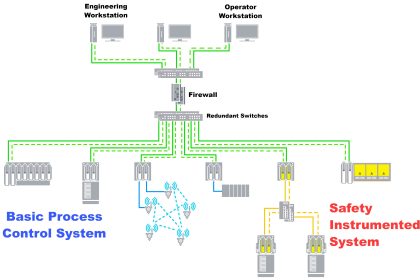
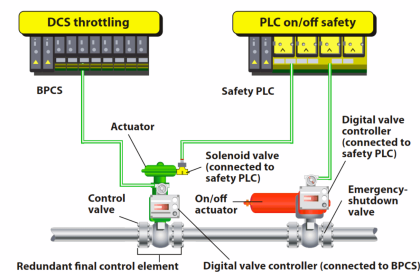
In the context of dependability (i.e. the probability that a safety component or system will function when called upon to act), the unreliability of that component or system is referred to as PFD, an acronym standing for Probability of Failure on Demand.
Probability of Failure on Demand

Like dependability, this is also a probability value ranging from 0 to 1, inclusive. A PFD value of zero (0) means there is no probability of failure (i.e. it is 100% dependable – guaranteed to properly perform when needed), while a PFD value of one (1) means it is completely undependable (i.e. guaranteed to fail when activated).
Thus:
Dependability + PFD = 1
PFD = 1 − Dependability
Dependability = 1 − PFD
Obviously, a system designed for high dependability should exhibit a small PFD value (very nearly 0). Just how low the PFD needs to be is a function of how critical the component or system is to the fulfillment of our human needs.
The degree to which a system must be dependable in order to fulfill our modern expectations is often surprisingly high. Suppose someone were to tell you the reliability of seat-belts in a particular automobile was 99.9 percent (0.999).
This sounds rather good, doesn’t it? However, when you actually consider the fact that this degree of probability would mean an average of one failed seat-belt for every 1000 collisions, the results are seen to be rather poor (at least to modern American standards of expectation). If the dependability of seat-belts is 0.999, then the PFD is 0.001:
PFD = 1 − Dependability
PFD = 1 − 0.999
PFD = 0.001
Let’s suppose an automobile manufacturer sets a goal of only 1 failed seatbelt in any of its cars during a 1 million unit production run, assuming each and every one of these cars were to crash.
Assuming four seatbelts per car, this equates to a 1/4000000 PFD. The necessary dependability of this manufacturer’s seatbelts must therefore be:
Dependability = 1 − PFD = 1 − (1/4000000) = 0.99999975
Thus, the dependability of these seatbelts must be 99.999975% in order to fulfill the goal of only 1 (potential) seatbelt failure out of 4 million seatbelts produced.
A common order-of-magnitude expression of desired reliability is the number of “9” digits in the reliability value. A reliability value of 99.9% would be expressed as “three nine’s” and a reliability value of 99.99% as “four nine’s.”
Expressed thusly, the seatbelt dependability must be “six nine’s” in order to achieve the automobile manufacturer’s goal.