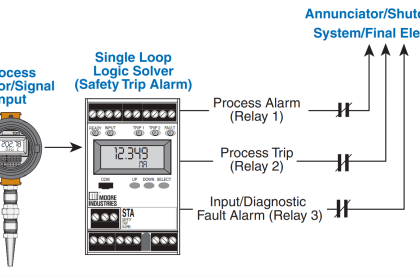
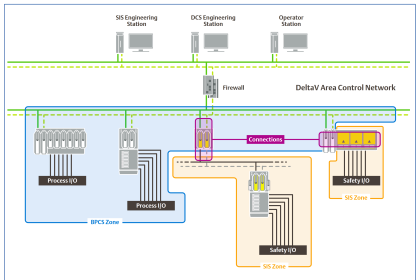
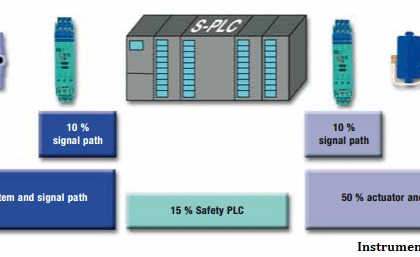
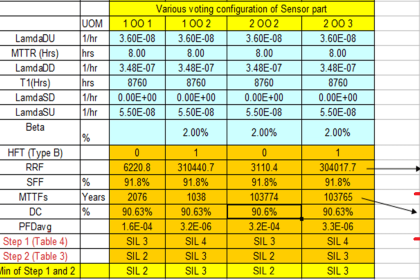
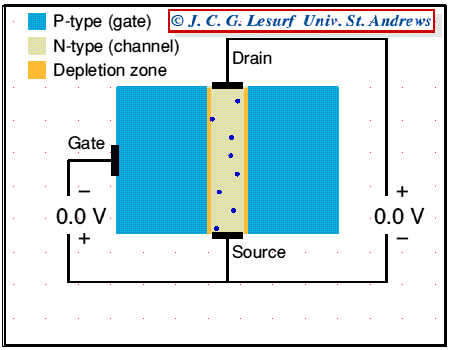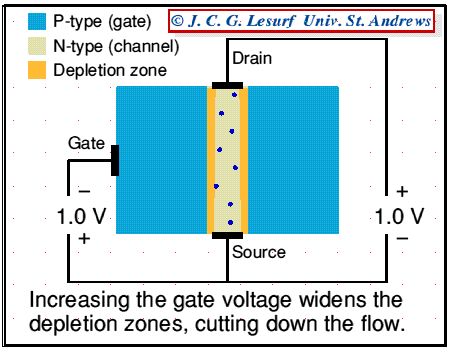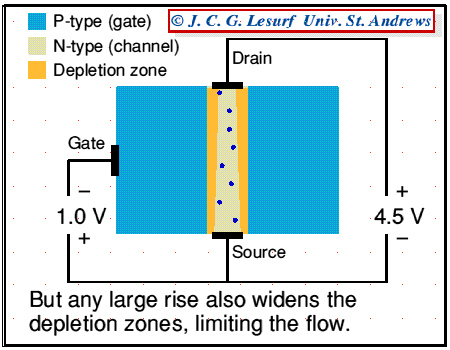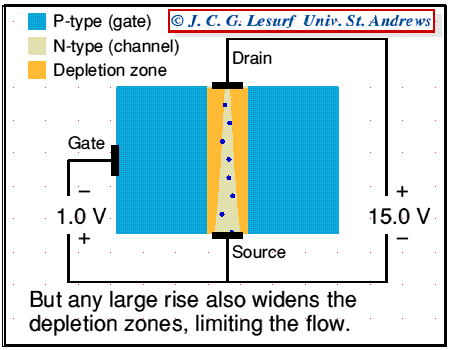
Reliability (R) is the probability a component or system will perform as designed. Like all probability figures, reliability ranges in value from 0 to 1, inclusive.
Reliability of a Control System

Given the tendency of manufactured devices to fail over time, reliability decreases with time. During the useful life of a component or system, reliability is related to failure rate by a simple exponential function:
R = e−λt
Where,
R = Reliability as a function of time (sometimes shown as R(t))
e = Euler’s constant (≈ 2.71828)
λ = Failure rate (assumed to be a constant during the useful life period)
t = Time
Knowing that failure rate is the mathematical reciprocal of mean time between failures (MTBF), we may re-write this equation in terms of MTBF as a “time constant” (τ ) for random failures during the useful life period:
R = e−t/MTBF or R = e−t/λ
This inverse-exponential function mathematically explains the scenario described earlier where we tested a large batch of components, counting the number of failed components and the number of surviving components over time.
Like the dice experiment where we set aside each “failed” die and then rolled only the remaining “survivors” for the next trial in the test, we end up with a diminishing number of “survivors” as the test proceeds.
The same exponential function for calculating reliability applies to single components as well. Imagine a single component functioning within its useful life period, subject only to random failures.
The longer this component is relied upon, the more time it has to succumb to random faults, and therefore the less likely it is to function perfectly over the duration of its test.
To illustrate by example, a pressure transmitter installed and used for a period of 1 year has a greater chance of functioning perfectly over that service time than an identical pressure transmitter pressed into service for 5 years, simply because the one operating for 5 years has five times more opportunity to fail. In other words, the reliability of a component over a specified time is a function of time, and not just the failure rate (λ).
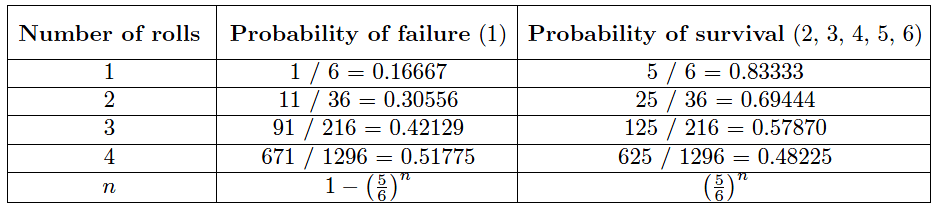
Using dice once again to illustrate, it is as if we rolled a single six-sided die over and over, waiting for it to “fail” (roll a “1”). The more times we roll this single die, the more likely it will eventually “fail” (eventually roll a “1”). With each roll, the probability of failure is 1/6 , and the probability of survival is 5/6 .
Since survival over multiple rolls necessitates surviving the first roll and and next roll and the next roll, all the way to the last surviving roll, the probability function we should apply here is the “AND” (multiplication) of survival probability.
Therefore, the survival probability after a single roll is 5/6 , while the survival probability for two successive rolls is ( 5/6)2 , the survival probability for three successive rolls is (5/6)3 , and so on.
The following table shows the probabilities of “failure” and “survival” for this die with an increasing number of rolls:
A practical example of this equation in use would be the reliability calculation for a Rosemount model 1151 analog differential pressure transmitter (with a demonstrated MTBF value of 226 years as published by Rosemount) over a service life of 5 years following burn-in:
R = e−5/226
R = 0.9781 = 97.81%
Another way to interpret this reliability value is in terms of a large batch of transmitters. If three hundred Rosemount model 1151 transmitters were continuously used for five years following burn-in (assuming no replacement of failed units), we would expect approximately 293 of them to still be working (i.e. 6.564 random-cause failures) during that five-year period:
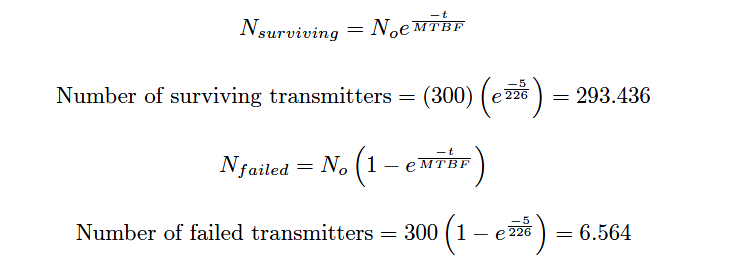
It should be noted that the calculation will be linear rather than inverse-exponential if we assume immediate replacement of failed transmitters (maintaining the total number of functioning units at 300).
If this is the case, the number of random-cause failures is simply 1/226 per year, or 0.02212 per transmitter over a 5-year period. For a collection of 300 (maintained) Rosemount model 1151 transmitters, this would equate to 6.637 failed units over the 5-year testing span:
Number of failed transmitters = (300) ( 5/226) = 6.637