In this article, you will learn the important factors in flow measurement which are quite useful for learning the basics of instrumentation.
Important Factors in Flow Measurement are viscosity, density, specific gravity, compressibility, head loss, discharge coefficient, and beta ratio.
Viscosity
Viscosity is defined as the quantitative measure of the tendency of a fluid to resist the forces of shear or deformation. Meaning, that a fluid that can flow easily (e.g. water) has low viscosity, and a fluid that resists flow (like cold honey, or Dunlop adhesive) is highly viscous.
The reference point for the viscosity scale is water at 20°C (68°F), which is equal to 1.0 centipoise. (1 poise = 1gm/cm s). The poise or centipoise is referred to as absolute viscosity.
Other units of viscosity used in the petroleum industries include Kinematics viscosity, expressed in Stokes (or centistokes) and Saybolt. Universal or Saybolt Furol viscosity expressed in seconds. These units are readily converted from one to the other when calculations require their use and values are given in other units.
The viscosity of a fluid depends primarily on temperature and to a lesser degree on pressure. The viscosity of liquids generally decreases with increasing temperature, and gas viscosity normally increases as temperature increases.
The effect of pressure on the viscosity of a liquid is very small, however, particularly at high pressure, it does affect the viscosity very significantly.
Density
The density of a substance is defined as its mass per unit volume.
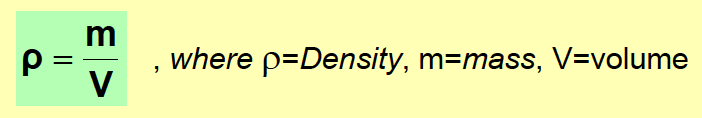
The unit derived from this formula is kg/m3. However, there are other units used, such as pounds per cubic inch, and ounces per gallon.
Liquid densities change considerably with temperature but are relatively very small with pressure because liquids are considered incompressible.
For gases and vapours, pressure and temperature are affected greatly by their densities. Therefore, in measuring the flow, the mass-flow measure is the most desired method to use.
Specific Gravity
Normally called ‘SG’, is the fluid weight (or mass) ratio to a standard one. For liquids (or solids), the standard referral is water (s.g. = 1.0) at 4°C (60°F).
For gases and vapours, the standard used is air (s.g. = 1.0) at 4°C (60°F) under atmospheric pressure (14.7 psi).

Specific gravity correction of flow
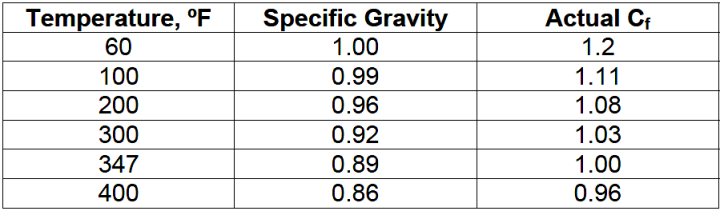
It is necessary to compensate for changes in specific gravity because of temperature.
The correction factor, Cf is used, multiplied against the D.P. (diff. pressure flowmeter) to provide the compensation.
Example:
Super-compressibility
Liquids are considered incompressible except at high-pressure ranges but it is normally not applicable to most liquid flow measurement methods.
However, for gases, the compressibility factor should be taken into consideration in its calculation since the percentage error is remarkably high.
The Compressibility Factor is a function of molecular weight, temperature, and pressure. Follow the following;
The Ideal Gas Law (Boyle’s + Charles Laws) ;
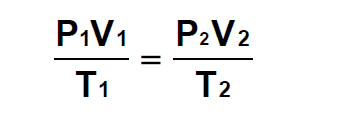
Assume at this moment, the gas is at a normal temperature and pressure. The molecules of gas are moving randomly constantly in the container.
When pressurized, the molecules have lost the space to move and become more attached to each other. These changes in the behavior of gas are called Super-compressibility (Z).
The general gas law was written to include the Z factor
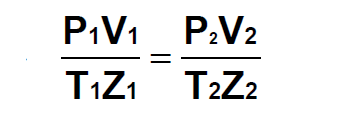
Head loss
Head loss occurs after a fluid passes through a restriction of an orifice or venturi, and does not quite return to its original pressure. Hydraulic energy cannot be transferred through pipes without losses.
Friction occurs at the pipe surface and within the liquid, which then generates heat. The loss created this way in hydraulic energy actually means that a pressure loss occurs within the system/pipe itself.
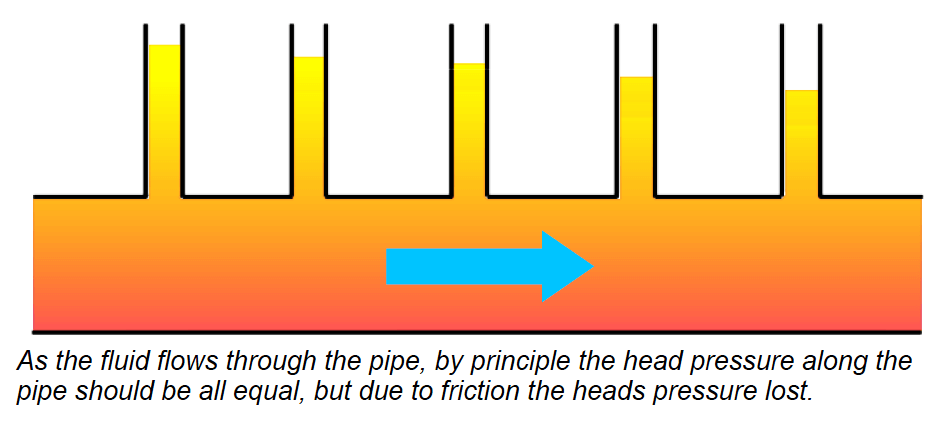
Discharge coefficient / Viscous friction
If we examine a real calibrated flow meter and plot recorded flow, against calculated flow, we find there is a constant difference over the whole flow range.
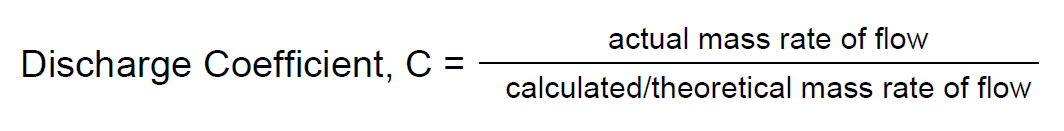
Note that C will normally be less than 1, the closer value to 1 the more ideal.
Typical values of C are; about 0.6 for an orifice plate, and about 0.99 for a venturi.
Beta ratio (β)
It is a ratio between the diameter of the orifice bore and the internal diameter of the pipe.
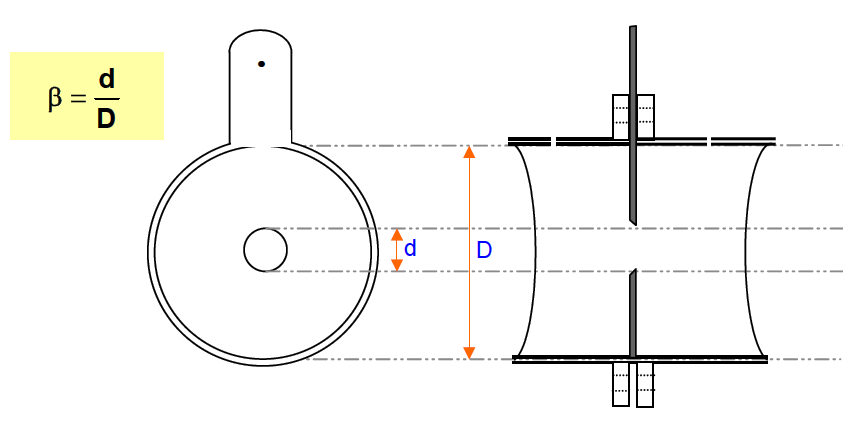
The range of β values is restricted to between 0.2 and up to 0.7 max. for accuracy and linearity in flow measurement.
Laminar and Turbulent fluid flow (Reynolds number)
Laminar refers to an orderly motion of flow where every particle of the fluid moves in parallel to the pipe.
However, the fluid flowing close to the wall slows down due to friction and viscosity.
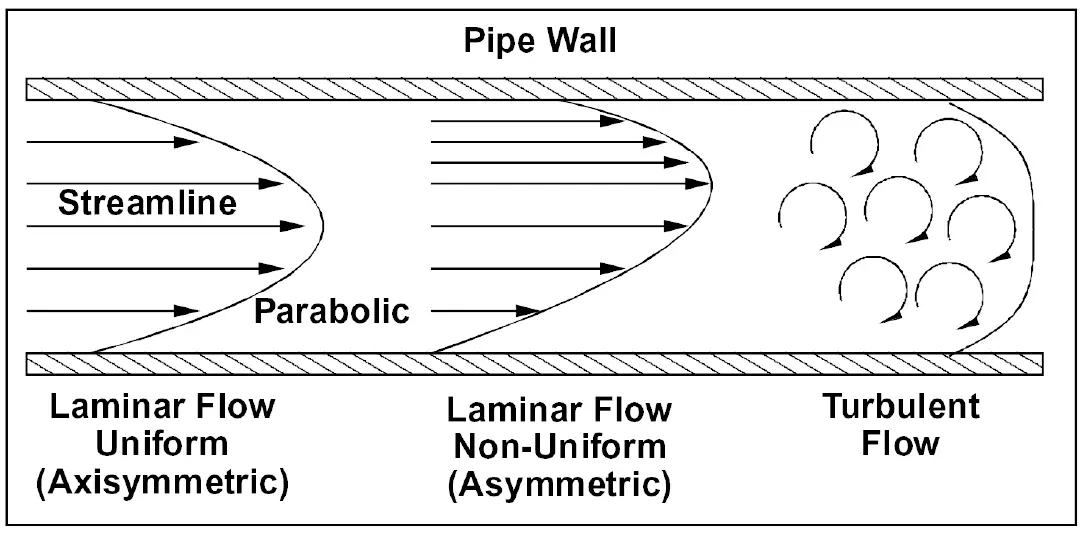
The flow is said to become turbulent when it speeds up even more. The two types can be demonstrated easily by injecting a small jet of colored water slowly into a clear liquid stream in a transparent pipe.
At a low flow rate, the colored water shows an even and with little diffusion in the surrounding stream. When a similar jet is released in a high-velocity stream, the diffusion is almost immediate and uniform across the section.
The Reynolds number (Re) tells us if the flow is laminar or turbulent;
- If less than 2000, it is laminar
- If more than 4000, it is turbulent
Reynolds Number is given by;

Therefore, Reynolds number depends on;
i. Velocity of the flow (velocity of the flow ∝ turbulence)
ii. Diameter of the pipe, D
iii. Density, ρ
iv. Viscosity of the liquid, η
Minimum and Maximum Volumetric Flow (Qmin/Qmax) Calculation
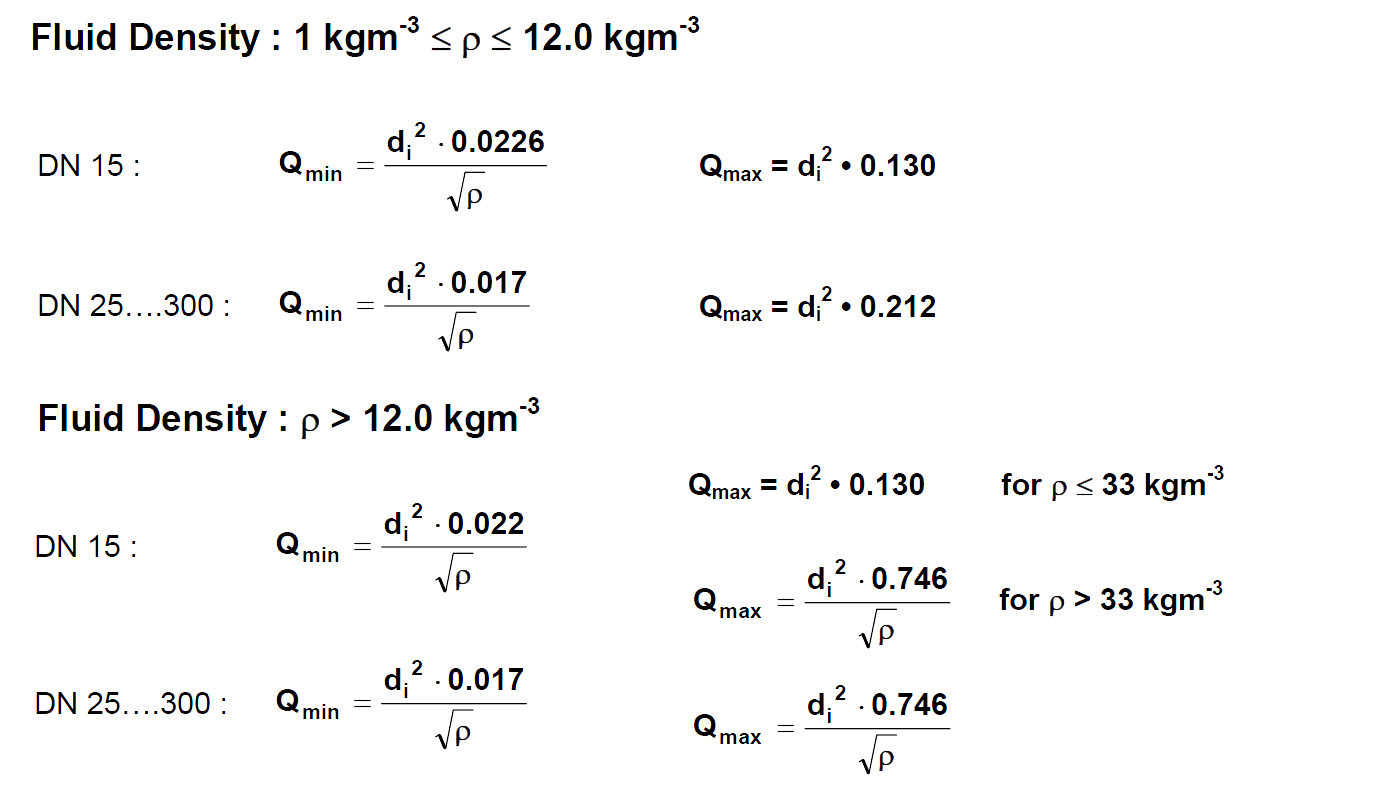
Where ;
- ρ = density in kgm-3
- Q = volumetric flow in m3/h
- di = internal diameter of pipe in mm
Credits: N Asyiddin
If you liked this article, then please subscribe to our YouTube Channel for Instrumentation, Electrical, PLC, and SCADA video tutorials.
You can also follow us on Facebook and Twitter to receive daily updates.
Read Next:
- Flow measurement Basics
- Flow meter Calibration
- Flow Meters Characteristics
- Vortex Flow Meter Theory
- Standard Temperature