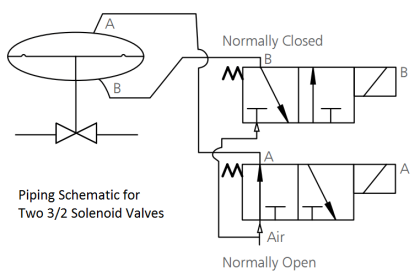
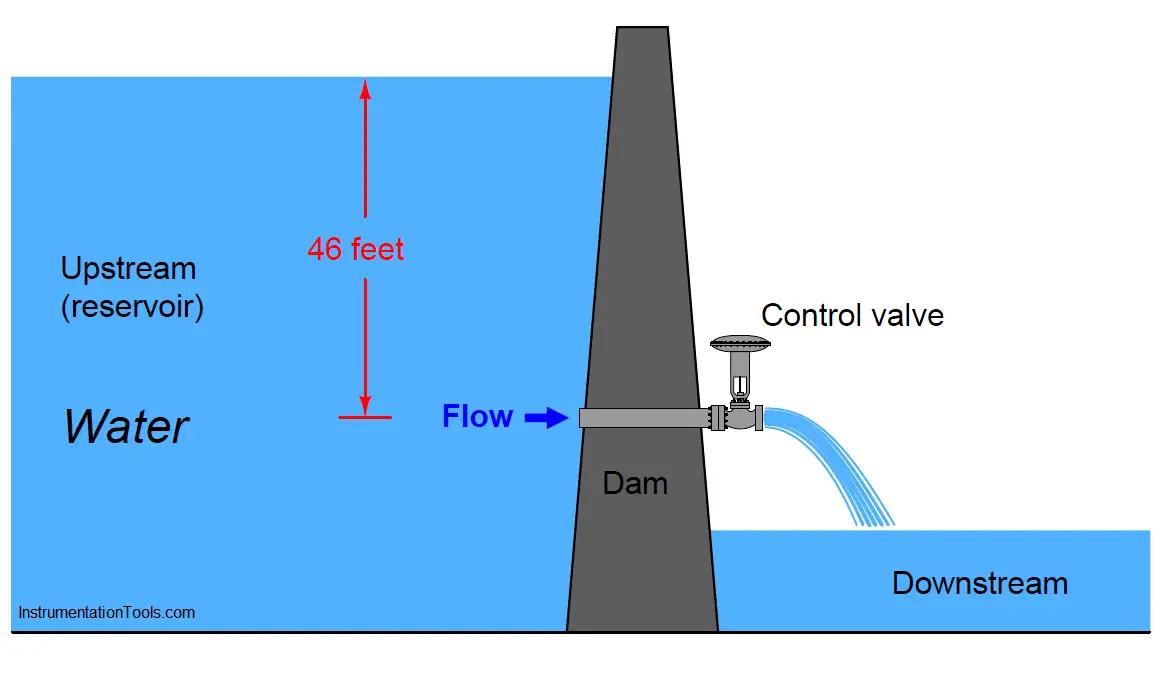
First, let us imagine a control valve installed at the base of a dam, releasing water from the reservoir. Given a constant height of water in the reservoir, the upstream (hydrostatic) pressure at the valve will likewise be constant.
Let’s assume this constant upstream pressure will be 20 PSI (corresponding to approximately 46 feet of water column above the valve inlet). With the valve discharging into the air, downstream pressure will essentially be zero.
This set of upstream and downstream conditions guarantees a constant pressure drop of 20 PSI across our control valve at all times, for all flow conditions:
Control Valve Performance with Constant Pressure
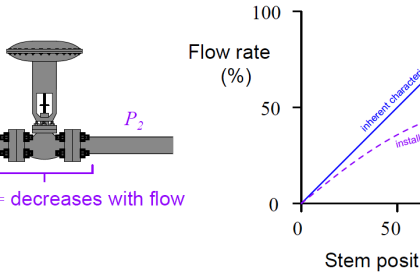
Furthermore, let us assume the control valve has a “linear” inherent characteristic and a maximum flow capacity (Cv rating) of 18. This means the valve’s Cv will be 18 at 100% open, 13.5 at 75% open, 9 at 50% open, 4.5 at 25% open, and 0 at fully closed (0% open).
We may plot the behavior of this control valve at these four stem positions by graphing the amount of flow through the valve for varying degrees of pressure drop across the valve.
The result is a set of characteristic curves (Note) for our hypothetical control valve:
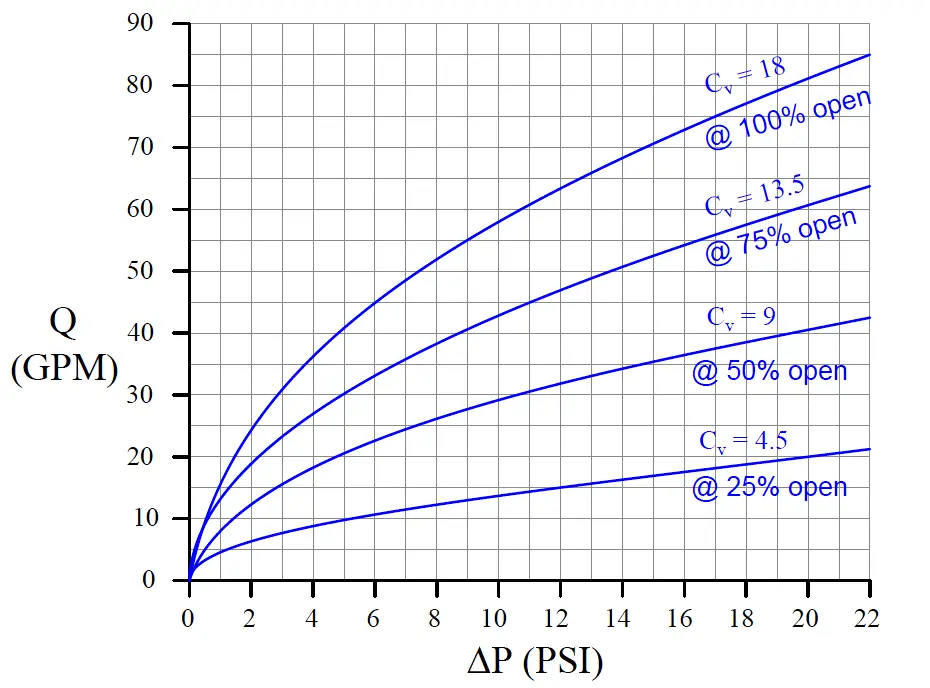
Note : For those readers with an electronics background, the concept of “characteristic curves” for a control valve is exactly the same as that of characteristic curves for transistors. Instead of plotting the amount of current a bipolar transistor will pass through its collector terminal (IC) given varying amounts of collector-emitter voltage drop (VCE), we are plotting the rate of water flow through the valve (Q) given varying amounts of supply pressure (ΔP).
Each curve on the graph traces the amount of flow through the valve at a constant stem position, for different amounts of applied pressure drop.
For example, looking at the curve representing 50% open (Cv = 9), we can see the valve should flow about 42 GPM at 22 PSI, about 35 GPM at 15 PSI, about 20 GPM at 5 PSI, and so on. Of course, we can obtain these same flow figures simply by evaluating the formula Q = Cv√ΔP (which is in fact what I used to plot these curves), but the point here is to learn how to interpret the graph.
We may use this set of characteristic curves to determine how this valve will respond in any installation by superimposing another curve on the graph called a load line, describing the pressure drop available to the valve at different flow rates.
Since we know our hypothetical dam supplies a constant 20 PSI across the control valve for all flow conditions, the load line for the dam will be a vertical line at 20 PSI:
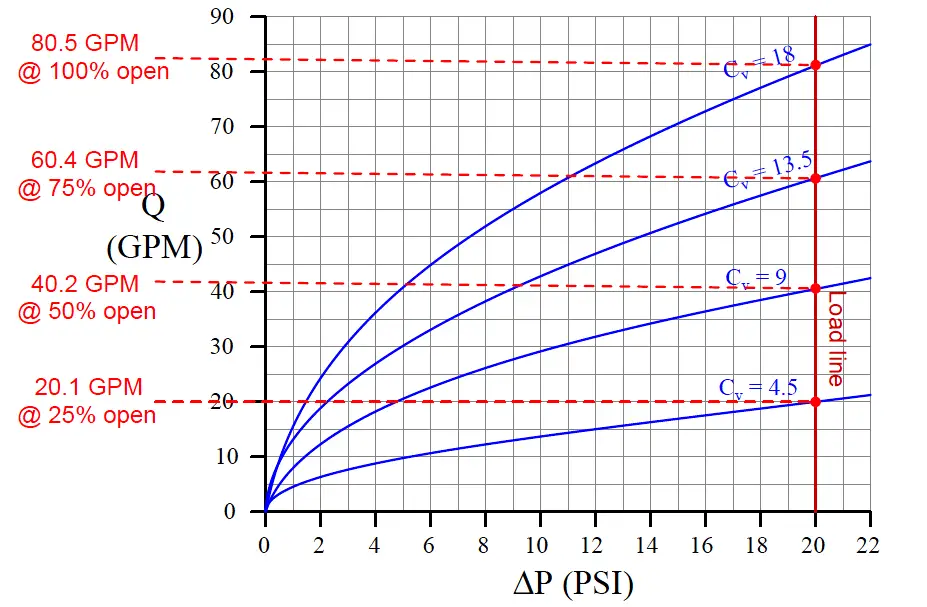
By noting the points of intersection between the valve’s characteristic curves and the load line, we may determine the flow rates from the dam at those stem positions:
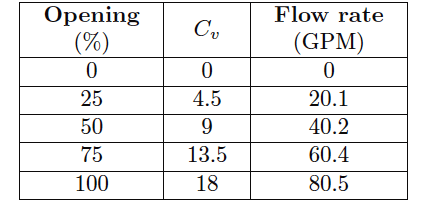
If we were to graph this table, plotting flow versus stem position, we would obtain a very linear graph. Note how 50% open gives us twice as much flow as 25% open, and 100% open nearly twice as much flow as 50% open.
This tells us our control valve will respond linearly when operated under these conditions (i.e. operating with a constant pressure drop).