Resistance in Parallel Circuits

Total resistance in a parallel circuit can be found by applying Ohm’s Law. Divide the voltage across the parallel resistance by the total line current as shown in below equation.

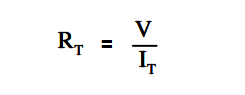
Example:

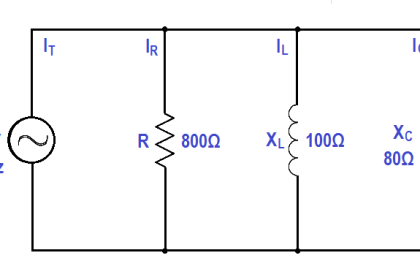
Find the total resistance of the circuit shown in Figure 25 if the line voltage is 120 V and total current is 26A.

Solution :

R_T = V/I_T

R_T = 120 / 26 = 4.62 Ω

The total load connected to a 120 V source is the same as the single “equivalent resistance” of 4.62Ω connected across the source (Figure 26). Equivalent resistance is the total resistance a combination of loads present to a circuit.

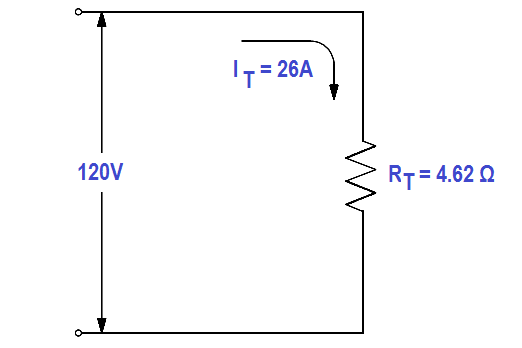
Figure 26 Equivalent Resistance in a Parallel Circuit

The total resistance in a parallel circuit can also be found by using the below equation.

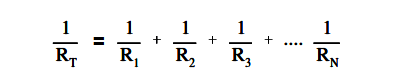
Example 1:

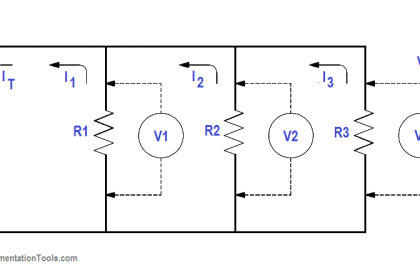
Find the total resistance of a 4Ω, and 8Ω ,and a 16Ω resistor in parallel (Figure 27).

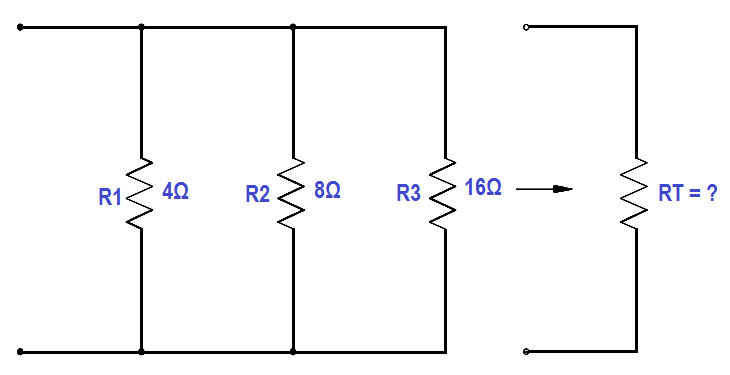
Figure 27 Total Resistance in a Parallel Circuit

Solution :

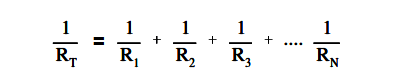
1 / R_T = 1/4 + 1/8 + 1/16

R_T = 16/7 = 2.29 Ω

Note: Whenever resistors are in parallel, the total resistance is always smaller than any single branch.

Example 2:

Now add a fourth resistance of 4Ω in parallel to the circuit in Figure 27. What is the new total resistance of the circuit?

Solution:

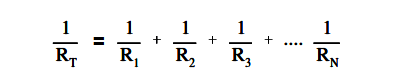
1 / R_T = 1/4 + 1/8 + 1/16 + 1/4

R_T = 16/11 = 1.45 Ω