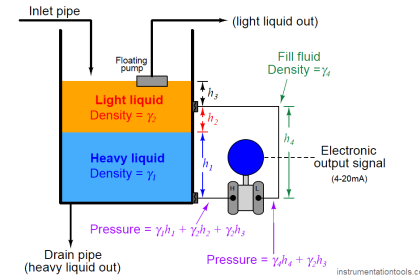
Displacer level instruments may be used to measure liquid-liquid interfaces just the same as hydrostatic pressure instruments. One important requirement is that the displacer always be fully submerged (“flooded”).
If this rule is violated, the instrument will not be able to discriminate between a low (total) liquid level and a low interface level. This criterion is analogous to the use of compensated-leg differential pressure instruments to measure liquid-liquid interface levels:
in order for the instrument to solely respond to changes in interface level and not be “fooled” by changes in total liquid level, both process connection points must be submerged.
If the displacer instrument has its own “cage,” it is important that both pipes connecting the cage to the process vessel (sometimes called “nozzles”) be submerged.
This ensures the liquid interface inside the cage matches the interface inside the vessel. If the upper nozzle ever goes dry, the same problem can happen with a caged displacer instrument as with a “sight glass” level gauge.
Calculating buoyant force on a displacer element due to a combination of two liquids is not as difficult as it may sound. Archimedes’ Principle still holds: that buoyant force is equal to the weight of the fluid(s) displaced.
All we need to do is calculate the combined weights and volumes of the displaced liquids to calculate buoyant force.
For a single liquid, buoyant force is equal to the weight density of that liquid (γ) multiplied by the volume displaced (V ):
Fbuoyant = γV
For a two-liquid interface, the buoyant force is equal to the sum of the two liquid weights displaced, each liquid weight term being equal to the weight density of that liquid multiplied by the displaced volume of that liquid:
Fbuoyant = γ1V1 + γ2V2
Assuming a displacer of constant cross-sectional area throughout its length, the volume for each liquid’s displacement is simply equal to the same area (πr2) multiplied by the length of the displacer submerged in that liquid:
Fbuoyant = γ1πr2l1 + γ2πr2l2
Since the area (πr2) is common to both buoyancy terms in this equation, we may factor it out for simplicity’s sake:
Fbuoyant = πr2(γ1l1 + γ2l2)
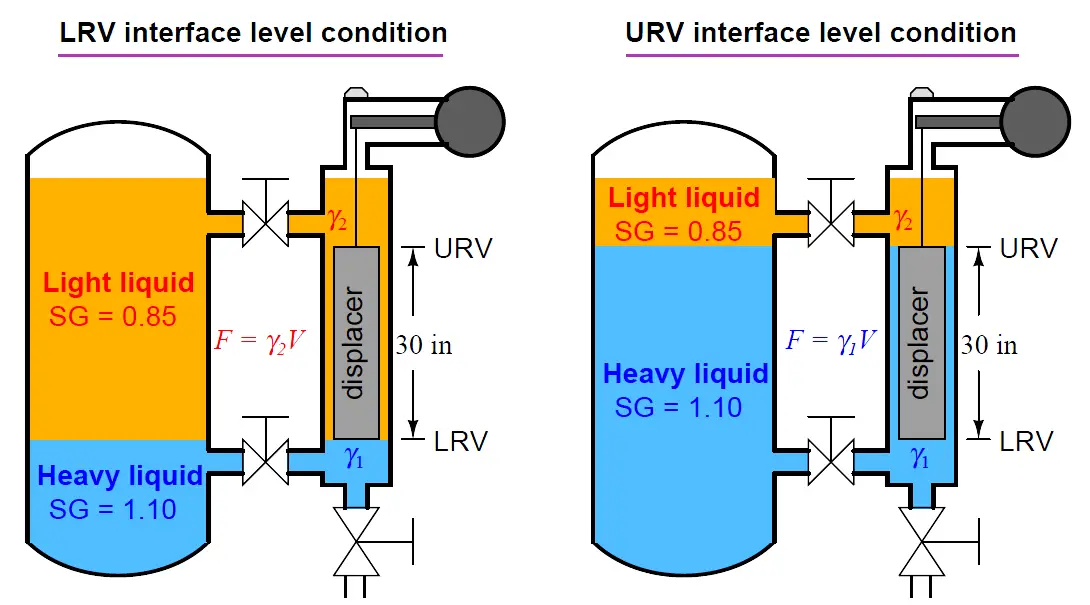
Determining the calibration points of a displacer-type level instrument for interface applications is relatively easy if the LRV and URV conditions are examined as a pair of “thought experiments” just as we did with hydrostatic interface level measurement.
First, we imagine what the displacer’s condition would “look like” with the interface at the lower range value, then we imagine a different scenario with the interface at the upper range value.
Sketching illustrations of each scenario is recommended for clarity.
Suppose we have a displacer instrument measuring the interface level between two liquids having specific gravities of 0.850 and 1.10, with a displacer length of 30 inches and a displacer diameter of 2.75 inches (radius = 1.375 inches).
Let us further suppose the LRV in this case is where the interface is at the displacer’s bottom and the URV is where the interface is at the displacer’s top.
The placement of the LRV and URV interface levels at the extreme ends of the displacer’s length simplifies our LRV and URV calculations, as the LRV “thought experiment” will simply be the displacer completely submerged in light liquid and the URV “thought experiment” will simply be the displacer completely submerged in heavy liquid.
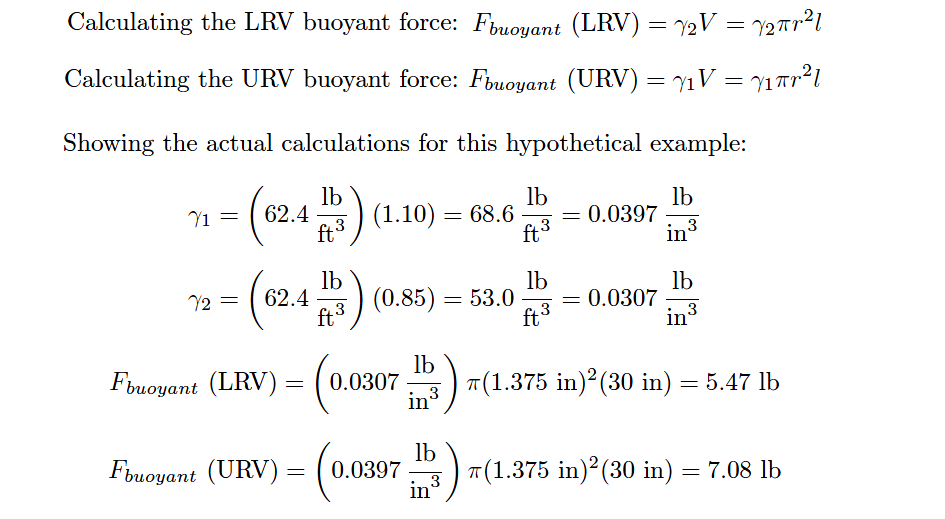
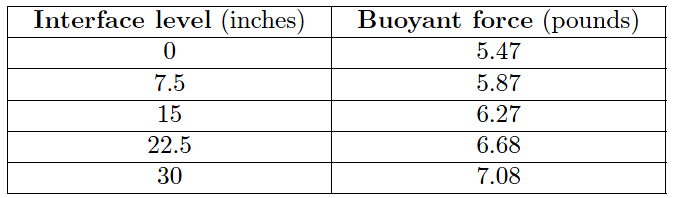
The buoyancy for any measurement percentage between the LRV (0%) and URV (100%) may be calculated by interpolation:
Credits : Tony R. Kuphaldt – Creative Commons Attribution 4.0 License










As long as you don’t use SI in your presentations, this site will remain of limited use, professionalism and importance ( ….. and it is what a pity! …)