Analysis of the AC power generation process and of the alternating current we use in almost every aspect of our lives is necessary to better understand how AC power is used in today’s technology.
Effective Values
The output voltage of an AC generator can be expressed in two ways. One is graphically by use of a sine wave (Figure 3). The second way is algebraically by the equation e = Emaxsin ωt, which will be covered later in the text.
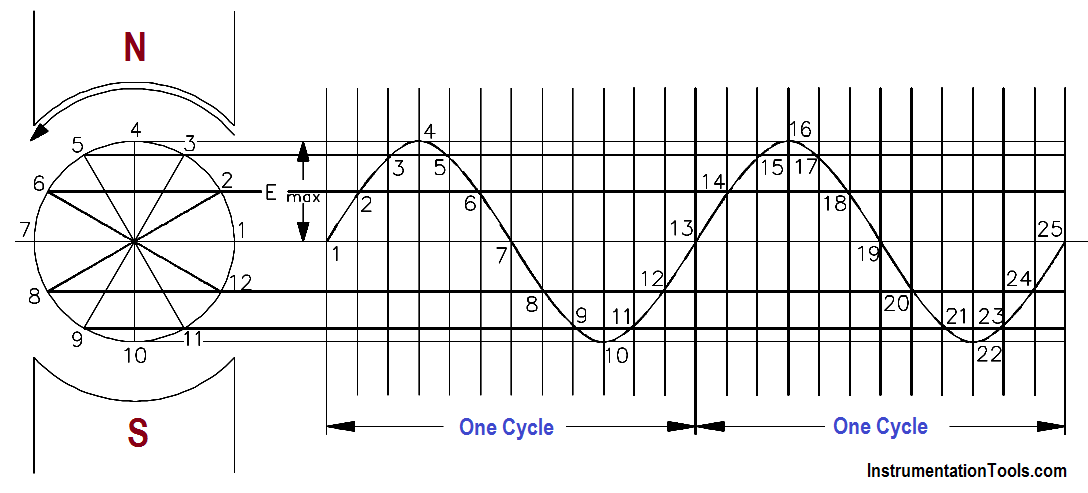
Figure 3 : Voltage Sine Wave
When a voltage is produced by an AC generator, the resulting current varies in step with the voltage. As the generator coil rotates 360°, the output voltage goes through one complete cycle. In one cycle, the voltage increases from zero to E in one direction, decreases to zero, increases to Emax in the opposite direction (negative Emax), and then decreases to zero again. The value of Emax occurs at 90° and is referred to as peak voltage. The time it takes for the generator to complete one cycle is called the period, and the number of cycles per second is called the frequency (measured in hertz).
One way to refer to AC voltage or current is by peak voltage (Ep ) or peak current (Ip ). This is the maximum voltage or current for an AC sine wave.
Another value, the peak-to-peak value (E p-p or Ip ), is the magnitude of voltage, or current range, spanned by the sine wave. However, the value most commonly used for AC is effective value. Effective value of AC is the amount of AC that produces the same heating effect as an equal amount of DC.
In simpler terms, one ampere effective value of AC will produce the same amount of heat in a conductor, in a given time, as one ampere of DC. The heating effect of a given AC current is proportional to the square of the current. Effective value of AC can be calculated by squaring all the amplitudes of the sine wave over one period, taking the average of these values, and then taking the square root. The effective value, being the root of the mean (average) square of the currents, is known as the root-mean-square, or RMS value. In order to understand the meaning of effective current applied to a sine wave, refer to Figure 4.
The values of I are plotted on the upper curve, and the corresponding values of I2 are plotted on the lower curve. The I2 curve has twice the frequency of I and varies above and below a new axis. The new axis is the average of the I2 values, and the square root of that value is the RMS, or effective value, of current. The average value is ½ Imax 2 . The RMS value is then
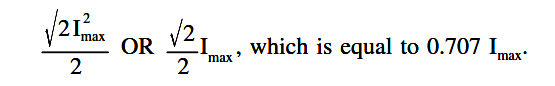
There are six basic equations that are used to convert a value of AC voltage or current to another value, as listed below.
- Average value = peak value x 0.637
- Effective value (RMS) = peak value x 0.707
- Peak value = average value x 1.57
- Effective value (RMS) = average value x 1.11
- Peak value = effective value (RMS) x 1.414
- Average value = effective (RMS) x 0.9
The values of current (I) and voltage (E) that are normally encountered are assumed to be RMS values; therefore, no subscript is used.
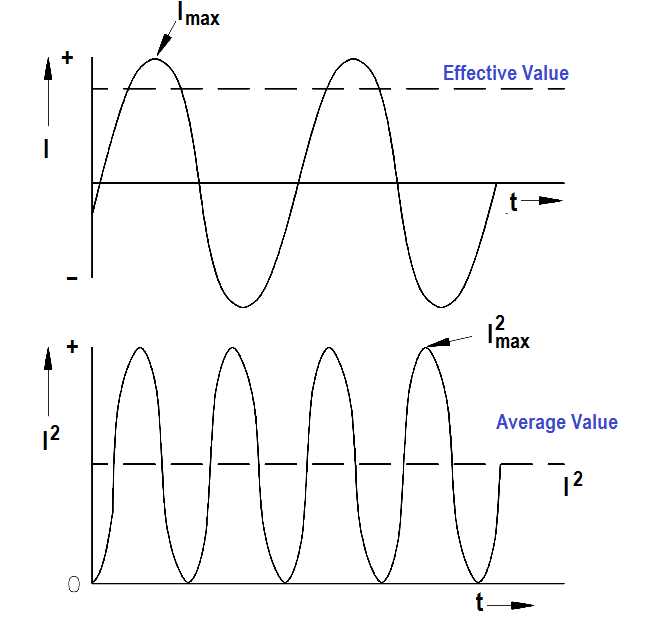
Figure 4 : Effective Value of Current
Another useful value is the average value of the amplitude during the positive half of the cycle.
The below Equation is the mathematical relationship between Iav , I max , and I.
Iav = 0.637 Imax = 0.9 I
The below Equation is the mathematical relationship between Eav , Emax , and E.
Eav = 0.637 Emax = 0.9 E
Example 1:
The peak value of voltage in an AC circuit is 200 V. What is the RMS value of the voltage?
E = 0.707Emax
E = 0.707 x 200 = 141.4 V
Example 2:
The peak current in an AC circuit is 10 amps. What is the average value of current in the circuit?
Iav = 0.637 Imax
Iav = 0.637 x 10 = 6.37 amps
Phase Angle
Phase angle is the fraction of a cycle, in degrees, that has gone by since a voltage or current has passed through a given value. The given value is normally zero. Referring back to Figure 3, take point 1 as the starting point or zero phase. The phase at Point 2 is 30°, Point 3 is 60°, Point 4 is 90°, and so on, until Point 13 where the phase is 360°, or zero. A term more commonly used is phase difference.
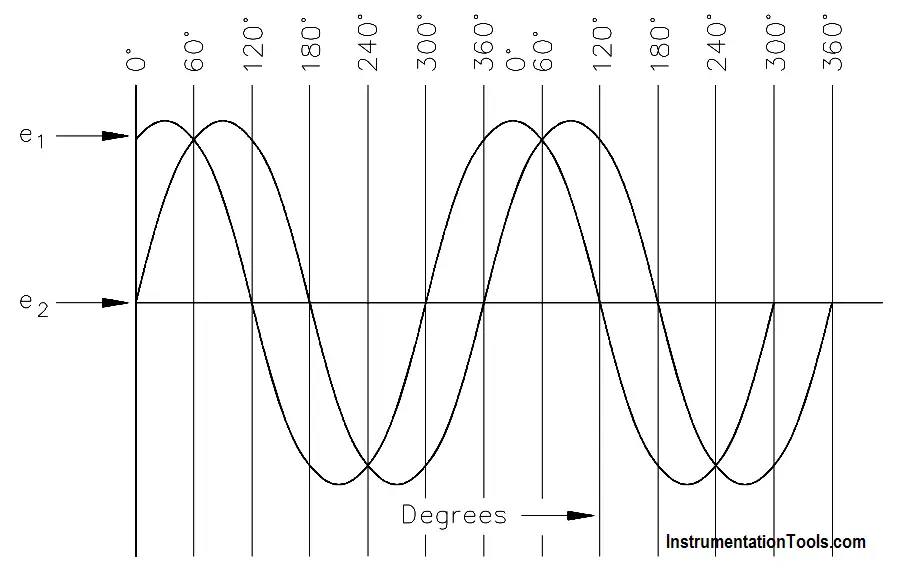
Figure 5 : Phase Relationship
The phase difference can be used to describe two different voltages that have the same frequency, which pass through zero values in the same direction at different times. In Figure 5, the angles along the axis indicate the phases of voltages e1 and e2 at any point in time.
At 120°, e1 passes through the zero value, which is 60° ahead of e2 ( e2 equals zero at 180°). The voltage e1 is said to lead e2 by 60 electrical degrees or it can be said that e2 lags e1 by 60 electrical degrees.
Phase difference is also used to compare two different currents or a current and a voltage. If the phase difference between two currents, two voltages, or a voltage and a current is zero degrees, they are said to be “in-phase.” If the phase difference is an amount other than zero, they are said to be “out-of-phase.”
Voltage Calculations
The below Equation is a mathematical representation of the voltage associated with any particular orientation of a coil (inductor).
e = Emax sinθ
where
e = induced EMF
Emax = maximum induced EMF
θ = angle from reference (degrees or radians)
Example 1:
What is the induced EMF in a coil producing a maximum EMF of 120 V when the angle from reference is 45°?
e = Emax sinθ
e= 120 v Sin (45)
e = 84.84 V
The maximum induced voltage can also be called peak voltage Ep . If (t) is the time in which the coil turns through the angle (θ), then the angular velocity (ω) of the coil is equal to θ/t and is expressed in units of radians/sec.
The below Equation is the mathematical representation of the angular velocity.
θ = ωt
where
ω = angular velocity (radians/sec)
t = time to turn through the angle from reference (sec)
θ = angle from reference (radians)
Using substitution laws, a relationship between the voltage induced, the maximum induced voltage, and the angular velocity can be expressed.
The below Equation is the mathematical representation of the relationship between the voltage induced, the maximum voltage, and the angular velocity, and is equal to the output of an AC Generator.
e = Emax sin(ωt)
where
e = induced EMF (volts)
Emax= maximum induced EMF (volts)
ω = angular velocity (radians/sec)
t = time to turn through the angle from reference (sec)
Current Calculations
Maximum induced current is calculated in a similar fashion. The below Equation is a mathematical representation of the relationship between the maximum induced current and the angular velocity.
i = Imax sin(ωt)
where
i = induced current (amps)
Imax= maximum induced current (amps)
ω = angular velocity (radians/sec)
t = time to turn through the angle from reference (sec)
Frequency Calculations
The frequency of an alternating voltage or current can be related directly to the angular velocity of a rotating coil. The units of angular velocity are radians per second, and 2π radians is a full revolution.
A radian is an angle that subtends an arc equal to the radius of a circle. One radian equals 57.3 degrees. One cycle of the sine wave is generated when the coil rotates 2π radians.
The below Equation is the mathematical relationship between frequency (f) and the angular velocity (ω) in an AC circuit.
ω = 2πf
where
ω = angular velocity (radians/sec)
f = frequency (HZ)
Example 1:
The frequency of a 120 V AC circuit is 60 Hz. Find the following: 1. Angular velocity 2. Angle from reference at 1 msec 3. Induced EMF at that point
Solution:
1. ω =2πf
ω = 2 (3.14) (60 Hz) = 376.8 radians/sec
2. θ = ωt
θ = (376.8 radian/sec) (.001 sec) = 0.3768 radians
3. e = Emax sinθ
e = (120 V) (sin 0.3768 radians)
e = (120 V) (0.3679)
e = 44.15 V