Voltmeters

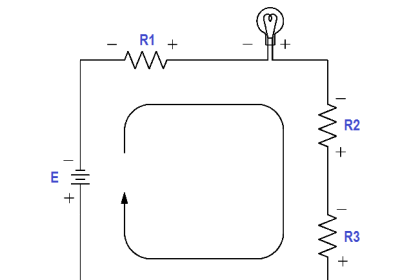
A simple DC voltmeter can be constructed by placing a resistor (R_S), called a multiplier, in series with the ammeter meter movement, and marking the meter face to read voltage (as shown in Figure).

Voltmeters are connected in parallel with the load (R_L) being measured.

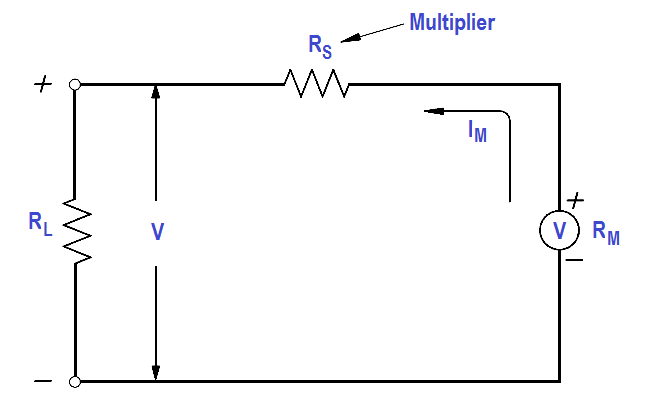
Figure : Simple DC Voltmeter

When constructing a voltmeter, the resistance of the multiplier must be determined to measure the desired voltage. The Equation is a mathematical representation of the voltmeter’s multiplier resistance.

V = I_mR_s + I_mR_m

I_mR_s = V – I_mR_m

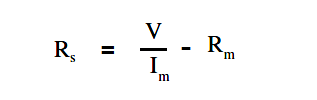
where

V = voltage range desired
I_m = meter current
R_m = meter resistance
R_s = multiplier resistance or series resistance

Example:

A 2 mA meter movement with internal resistance of 25 ohms is to be constructed as a voltmeter. What value must the series resistance be to measure full scale voltage of 100 volts?

Solution :

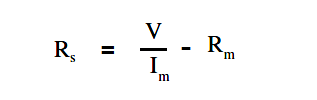
Since R_m is negligibly low, then

R_s = V/I_m

R_s = 100 / (2×10^-3)

R_s =  50kΩ

When a voltmeter is connected in a circuit, the voltmeter will draw current from that circuit. This current causes a voltage drop across the resistance of the meter, which is subtracted from the voltage being measured by the meter. This reduction in voltage is known as the loading effect and can have a serious effect on measurement accuracy, especially for low current circuits.

The accuracy of a voltmeter (K_v ) is defined as the ratio of measured voltage when the meter is in the circuit (V_w) to the voltage measured with the meter out of the circuit.

The below Equation is a mathematical representation of the accuracy of a voltmeter, or true voltage (V_o).

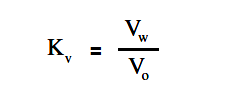
Meter accuracy can also be determined by comparing the relationship between the input and circuit resistances using Ohm’s Law as described below.

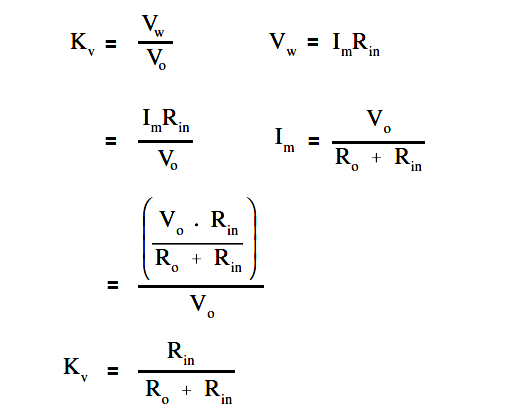
where

I_m = meter current
V_o = true voltage
R_o = circuit resistance
R_in = input resistance of the voltmeter
V_w = indicated voltage
K_v = meter accuracy

Example:

A voltmeter in the 100 volt range with a sensitivity of 40 KΩ/V is to measure the voltage across terminals ab.

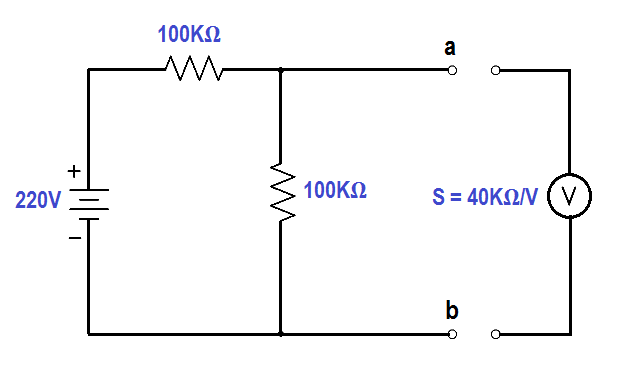
Find :

1. V_o , true voltage
2. V_w , indicated voltage
3. K_v , meter accuracy

Solution :

Find V_o , true voltage

V_o =  { 100 KΩ / (100 KΩ + 100 KΩ) } x 220 volts

V_o = 110 volts

Find V_w , indicated voltage

R_o = (100 x 100) / (100 + 100) = 50KΩ

R_in = S V = 40KΩ x 100 = 4.4 MΩ

V_w = R_in / (R_{o + Rin )}

V_w = { 4.4MΩ / (50KΩ + 4.4MΩ) } 110 volts

V_w = 108.9 volts

Find K_v , meter accuracy

K_v = V_w / V_o

K_v = 108.9/110

K_v = 0.99 or 99%