A very common technique in industrial instrumentation is to calculate the value of a process variable from the values of related variables which are easier to measure (Note 1 ) . As it so happens, there are a host of variables which one may infer from readings of differential pressure. This makes DP transmitters very versatile devices, not just limited to measuring process variables of pressure and vacuum. This portion of the book will explore some of the more common inferred measurements possible with DP instruments.
Note 1 : Truth be told, most process variables are inferred rather than directly measured. Even pressure, which is being used here to infer measurements such as liquid level and fluid flow, is itself inferred from some other variable inside the DP instrument (e.g. capacitance, strain gauge resistance, resonant frequency)!
Inferring liquid level
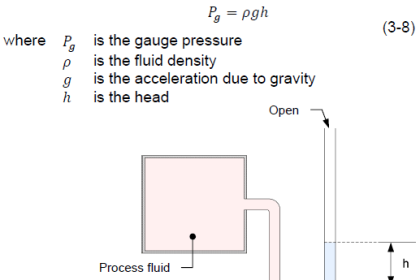
Liquids generate pressure proportional to height (depth) due to their weight. The pressure generated by a vertical column of liquid is proportional to the column height (h), and liquid’s mass density (ρ), and the acceleration of gravity (g):
P = ρgh
Knowing this, we may use a DP transmitter as a liquid level-sensing device if we know the density of the liquid remains fairly constant (We simply assume Earth’s gravitational acceleration (g) to be constant as well.)
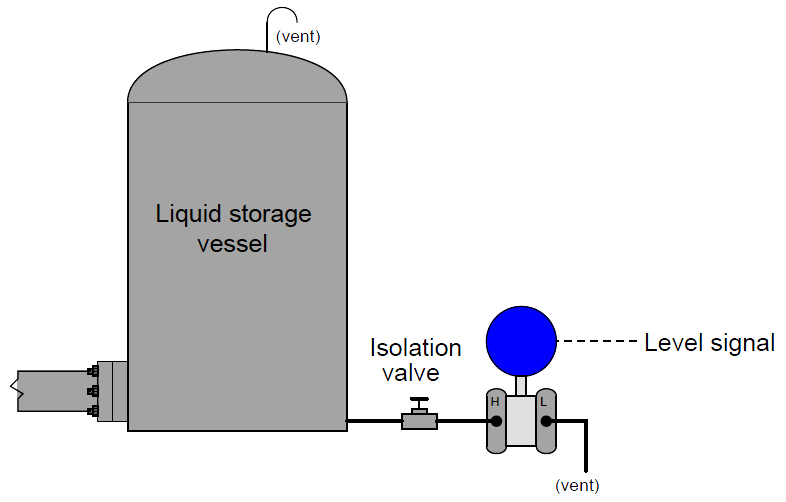
As liquid level in the vessel increases, the amount of hydrostatic pressure applied to the transmitter’s “high” port increases in direct proportion. The width of the vessel is irrelevant to the amount of pressure produced – only the liquid height (h), density (ρ), and Earth’s gravity (g) are significant. Thus, the transmitter’s increasing signal represents the height of liquid inside the vessel, no matter the size or shape of the vessel:
h = P / ρg
This simple technique works even if the vessel is under pressure from a gas or a vapor (rather than being vented as was the case in the previous example). All we need to do to compensate for this other pressure is to connect the DP transmitter’s “low” port to the top of the vessel so it senses nothing but the gas pressure:
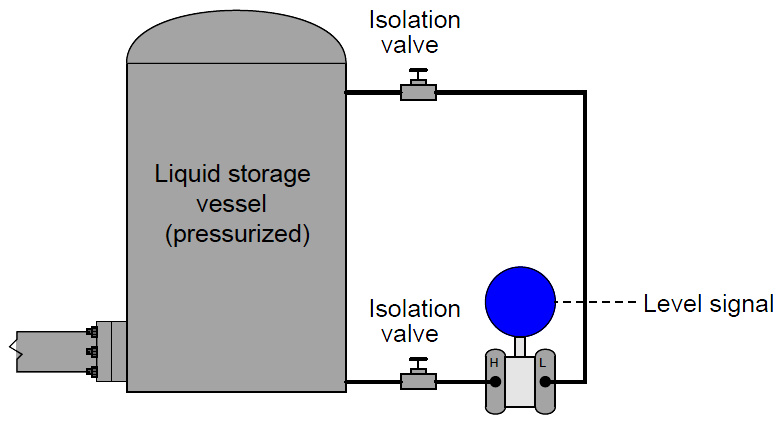
Since the transmitter responds only to differences of pressure between its two sensing ports, and the only cause for a difference of pressure in this application will be pressure generated by the height of a liquid column, the transmitter’s signal becomes an exclusive representation of liquid level in the vessel, rejecting potential measurement errors caused by changes in gas pressure within the vessel.
Any gas pressure within the vessel will be sensed equally by both ports on the transmitter as a “common-mode” pressure, thus canceling each other and having no effect on the differential pressure measurement. Only changes in liquid level within the vessel will cause the “high” port pressure to change independently of the “low” port pressure, changing the transmitter’s output signal.
Inferring gas and liquid flow
Another common inferential measurement using DP transmitters is the measurement of fluid flow through a pipe. Pressure dropped across a constriction in the pipe varies in relation to flow rate (Q) and fluid density (ρ). So long as fluid density remains fairly constant, we may measure pressure drop across a piping constriction and use that measurement to infer flow rate.
The most common form of constriction used for this purpose is called an orifice plate, being nothing more than a metal plate with a precisely machined hole in the center. As fluid passes through this hole, its velocity changes, causing a pressure drop to form:
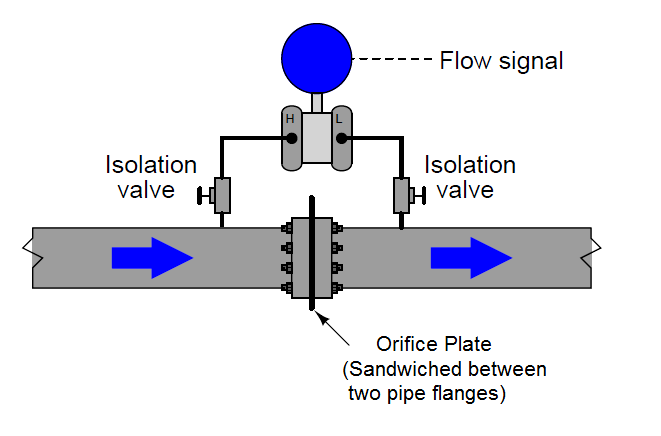
Once again, we see the common-mode rejection abilities of the pressure transmitter used for practical advantage. Since both ports of the transmitter connect to the same process line, static fluid pressure within that line has no effect on the measurement. Only differences of pressure between the upstream and downstream sides of the constriction (orifice plate) cause the transmitter to register flow.
Credits : Tony R. Kuphaldt – Creative Commons Attribution 4.0 License