What is a fluid?
Matter can exist in several states. These states are known as the physical states or the states of matter. The first three states of matter are well known because we can experience them in everyday life. They are the solid, the liquid, and the gaseous states (Figure 3- 3). The “other” states are not of interest for now, since they only occur in extreme physical conditions.
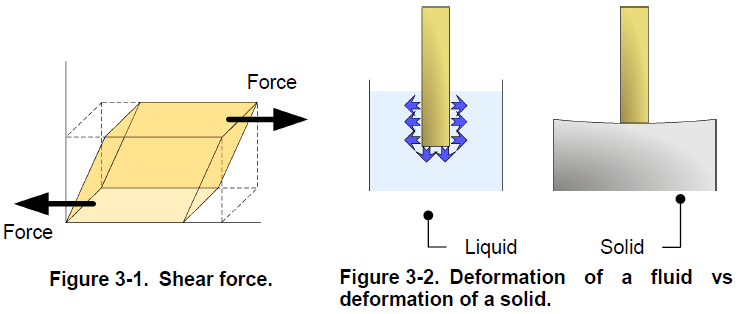
Matter, either in its liquid or gaseous state, is a fluid and, although liquids and gases react differently in some circumstances, they share the main characteristics of fluids. That is, a fluid deforms continuously when a shear force is exerted upon it. Unlike solids, which do not deform much in response to a force, fluids flow away and continue to deform as long as the force is exerted (Figure 3-2). When confined in a closed container, a fluid takes the shape of the container. A confined liquid occupies only the bottom of the container, not all the space available like a gas.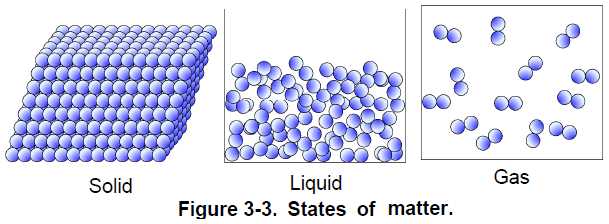
The continuum hypothesis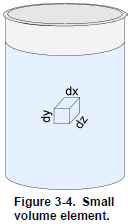
Like solids, fluids are made of molecules interacting with each other. It is virtually impossible to track the speed and position of each of these molecules, and therefore an assumption is made to simplify the models and calculations in fluid mechanics. This assumption is the continuum hypothesis, it supposes that the influence of the individual characteristics of molecules is negligible compared to the characteristics of the whole fluid. Thus, considering the continuum hypothesis, a small volume element ( ∙ ∙ ) has defined properties such as pressure, temperature, density, and velocity (Figure 3-4). The continuum hypothesis also requires that these properties vary continuously between two adjacent volume elements. Hence, the continuum hypothesis requires that the fluid is assumed to be continuous over its entire volume instead of being made up of individual molecules.
What are the main characteristics of fluids?
The four main characteristics of fluids are density, specific gravity, dynamic viscosity, and vapor pressure. This section provides details about these four characteristics.
Density
The density of a fluid is the ratio of its mass per unit of volume, that is
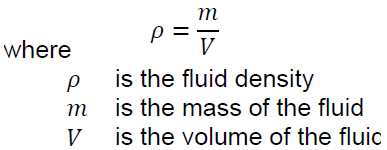
The density of a substance varies with pressure. This variation is usually small for liquids and solids, but it is important for gases since they are very compressible. An increase in the pressure applied on a gas greatly affects its density. In contrast, liquids are relatively incompressible and an increase in pressure does not change their density significantly. Density has units of kilograms per cubic meter (kg/m3) in SI units and of pounds per cubic foot (lb/ft3) in US customary units.
The density of solids and liquids also changes with temperature, refer to a density as a function of temperature table if you need the density of a sub-stance at a specific temperature.
Specific gravity
Specific gravity, or relative density, is the ratio of the density of a substance to the density of an equal volume of water:

Since density varies with temperature and pressure, specific gravity is usually measured at 4°C (39.4°F) and at normal atmospheric pressure. At these conditions, the density of water is 1000 kg/m3 (62.4 lb/ft3). Since a ratio is a dimensionless number, specific gravity has no units.
Dynamic viscosity
The viscosity of a fluid is its capacity to resist deformation. Incidentally, viscosity gives a measure of how easily a liquid flows. Dynamic viscosity has units of pascal-second (Pa·s) in SI units and of pound-force per foot second (lbf/ft·s) in US customary units. Dynamic viscosity is sometimes measured in the C.G.S. units of poises (P), where 1 P is equal to 0.1 Pa· s or 0.067 lbf/ft·s. Temperature has a significant effect on viscosity. The viscosity of liquids decreases when their temperature increases, unlike the viscosity of gases, which increases with temperature.
Vapor pressure
Vapor pressure is the pressure developed by the vapor of a fluid or a solid. Vapor pressure is measured for a given temperature when the vapor is at equilibrium with the solid or liquid phase of the substance. Vapor pressure is a pressure, thus it has units of kilopascals (kPa) in SI units and pounds per square inch (psi) in US customary units.
Compressibility
Another difference between liquids and gases is their compressibility. Compressibility is the capacity of a fluid to decrease in volume when subjected to pressure. Liquids are relatively incompressible while gases can be compressed. The near-incompressibility of liquids implies that their pressure increases rapidly when they are confined and pushed on. Hydraulic systems use this property of liquids to develop very high pressure and transmit tremendous amounts of power to other elements.
Hydrostatic pressure
Pressure is the amount of force exerted per unit of area: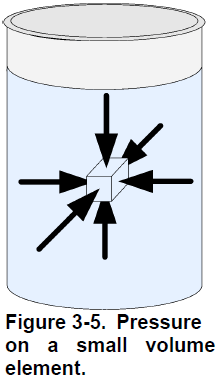
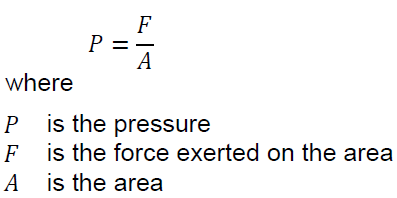
An ideal fluid cannot exert a shear force; thus, the forces on a small volume element are equal normal forces only, as Figure 3-5 shows. At rest, the
pressure that a fluid exerts on a small volume element depends only on the weight of the fluid above this element. The pressure due to the weight of liquid is proportional to the depth at which the pressure is measured, and only to this depth. The shape of the vessel has no influence on the hydrostatic pressure. For example, if two tanks are full of water but have a different diameter, the hydrostatic pressure due to the weight of water is the same at the bottom of both tanks (Figure 3-6).
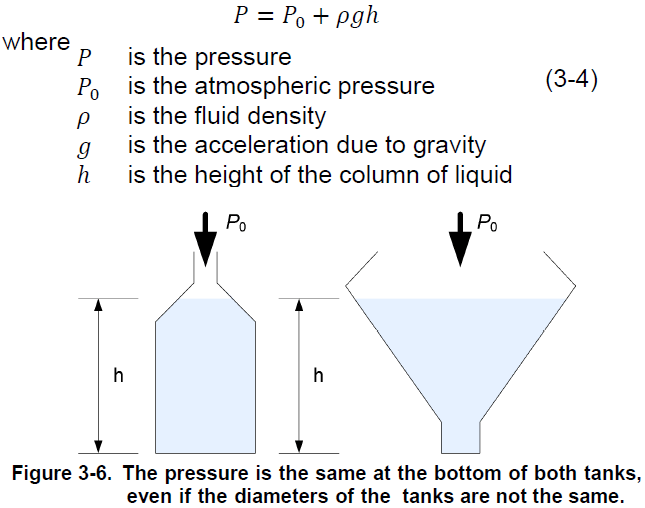
The absolute pressure at the bottom of a column of liquid is the sum of the atmospheric pressure and the hydrostatic pressure due to the weight of liquid. The mathematical expression used to calculate the pressure at the bottom of a vessel is
Pascal’s Law
Blaise Pascal (1623-1662) the French mathematician, physicist, and philosopher, deduced from the fact that a column of fluid exerts a pressure that varies only with the height of the column of fluid, that
An external pressure applied to a confined fluid is conveyed undiminished to every part of the fluid.
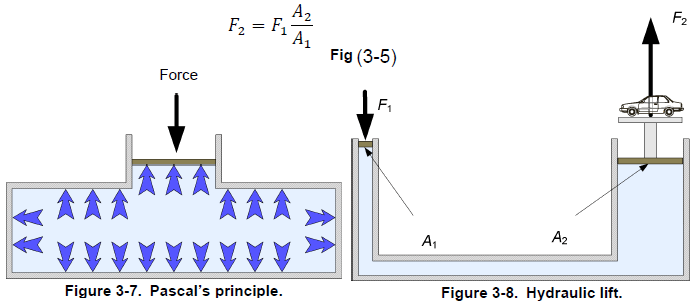
Figure 3-7 illustrates Pascal’s law, also known as Pascal’s principle. An application of this principle is the hydraulic lift (Figure 3-8). Using two pistons of different areas (A1 and A2), the force on the first piston (F1) is multiplied by the ratio of the area of the two pistons to produce a larger output force (F2). Thus, the output force is F2 calculated and equation shown in above figure.
Pressure measurement
Units of measurement of pressure
The equipment provided with the Instrumentation and Process Control Training System provides pressure readings in SI units and US customary units. The SI unit of pressure is the pascal (Pa). One pascal (1 Pa) is one newton (1 N) of force applied to an area of one square meter (1 m2). Therefore, 1 Pa is equal to 1 N/m2. Since most measurements are of the order of magnitude of 1×103 Pa, most instruments give readings with units of kilopascal (kPa) instead of pascal, where one kilopascal (1 kPa) is equal to 1000 Pa. In US customary units, pressure has units of pounds-force per square inch (psi). One pound-force per square inch (1 psi) is one pound of force (1 lbf) applied to an area of one square inch (1 in2). Some instruments also give readings using other units such as bar (bar). One bar (1 bar) is equal to 100 kPa or 14.5 psi.
Pressure head
As previously mentioned, the hydrostatic pressure at one point in a vessel depends on the height of liquid above this point. For two points in a vessel, the pressure difference, ∆ , is proportional to the distance, h, between these two points (Figure 3-9). Thus, the pressure difference is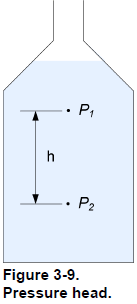
![]()
This simple relationship, between the pressure and the height of a column of liquid, provides a convenient way to express a pressure difference as the height of a column of liquid:

The height a column of liquid must have to produce a given pressure is the head or pressure head. For a given pressure, the equivalent height of water is not the same as the equivalent height of mercury. This is because the pressure head varies with the density of the liquid; therefore, you must specify the type of liquid used as reference as well as the temperature when expressing a pressure as the height of a column of liquid. For high pressure, the equivalent height of a column of liquid is very high, too high to be useful for comparison. For example, 1000 kPa (145 psi) is equivalent to 102 meters of water (4015 inches of water). For this reason, pressure head is primarily used to measure low pressure. Pressure head has units of meters (m) or centimeters (cm) of water or mercury. In US customary units the feet (ft) or inches (in) of water or mercury are common units for pressure head. A pressure of 1 kPa corresponds to a head of 0.102 m of water at 4°C. Consequently, a 0.102 m column of water at 4°C produces a pressure of 1 kPa at its bottom. Similarly, a pressure of 1 psi corresponds to a head of 27.7 in of water at 39°F. Consequently, a 27.7 in column of water at 39°F produces a pressure of 1 psi at its bottom.
Types of pressure measurements
A pressure is always measured relative to a reference pressure. The reference pressure can be either a vacuum or atmospheric pressure. You can also choose to measure a pressure relative to another pressure.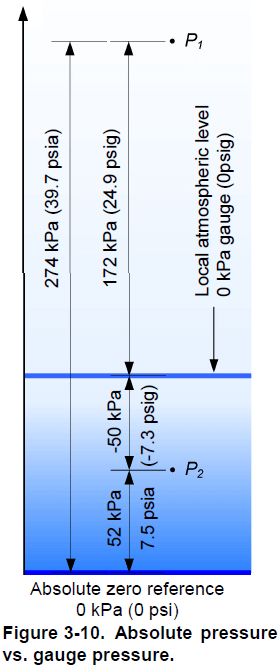
Absolute pressure
The word vacuum comes from the Latin word vacuus, which means empty. A vacuum is a space absolutely devoid of matter, and because there must be matter to create pressure, there is no pressure in a vacuum. Therefore, the vacuum pressure is exactly 0 kPa (0 psi). A pressure measured with respect to vacuum pressure is an absolute pressure. An absolute pressure is always positive since its reference pressure is 0 kPa (0 psi) . The SI unit of an absolute pressure is the pascal, however when you refer to an absolute pressure, you must specify that it is an absolute pressure (ex: the gas in the tank is at an absolute pressure of 300 kPa). In US customary units, an absolute pressure has units of pounds per square inch, absolute, which is abbreviated psia (ex: the gas in the tank is at a pressure of 43.5 psia).
Gauge pressure
Instead of using vacuum as a reference for pressure measurement, most instruments use the local atmospheric pressure as the reference. At sea level, the average pressure due to the weight of the air is 101,325 Pa or 101.3 kPa (14.7 psia). Locally, the atmospheric pressure depends on the altitude of the location and of the actual atmospheric conditions. The difference between the measured pressure and the local atmospheric pressure is the gauge pressure . A gauge pressure reading corresponds to the absolute pressure reading minus the local atmospheric pressure. The gauge pressure is zero if the measured pressure equals the local atmospheric pressure; it is negative if the measured pressure is below the local atmospheric pressure and positive if it is above. The SI unit of a gauge pressure is the pascal; however, as in the case of an absolute pressure, you must specify that you refer to a gauge pressure (ex: the gas in the tank is at a gauge pressure of 200 kPa). In US customary units, a gauge pressure has units of pounds per square inch, gauge, which is abbreviated psig (ex: the gas in the tank is at a pressure of 29 psig). Figure 3-10 shows the difference between an absolute pressure and a gauge pressure.
Differential pressure
Some pressure measurement devices measure the pressure at two points and give the pressure difference as the result. The pressure difference between two points is often referred to as the differential pressure. A pressure gauge is an example of a differential pressure measurement device because it measures the difference between the measured pressure and the atmospheric pressure. The SI unit for a differential pressure is the pascal. For additional clarity, you can specify that it is a differential pressure (ex: the differential pressure between the top and the bottom of the tank is 200 kPa). In US customary units, a differential pressure has units of pound per square inch, differential, which is abbreviated psid (ex: the differential pressure between the top and the bottom of the tanks is 29 psid).
Brief Definitions:
Atmospheric Pressure
Atmospheric pressure is the force of pressure exerted by the earthÕs atmosphere. Atmospheric pressure at sea level is equivalent to 14.695 psia. The value of atmospheric pressure decreases with increasing altitude.
Barometric Pressure
Barometric pressure is the same as atmospheric pressure.
Hydrostatic Pressure
Hydrostatic, pressure is encountered in liquid level applications. Hydrostatic pressure is the pressure below the liquid surface exerted by the liquid above.
Line Pressure
Line pressure is simply the amount of pressure, or the force per unit area, exerted on a surface by the ß ow parallel to a pipe wall.
Static Pressure
Static pressure is the same as line pressure.
Working Pressure
Working pressure is also referred to as line or static pressure.
Absolute Pressure
Absolute pressure is a single pressure measurement with a reference to a full, or perfect vacuum. Absolute pressure is the measurement of the process pressure in excess of full vacuum or 0 psia. Zero absolute pressure (0 psia) represents a total lack of pressure- For example, space is considered to be a full vacuum.
Gauge Pressure
Gauge pressure is a single pressure measurement that indicates the pressure above atmosphere. Gauge pressure represents the positive difference between measured pressure and existing atmospheric pressure. You can convert gauge pressure to absolute pressure by adding the actual atmospheric pressure value to the gauge pressure reading. For example 10 psig is equivalent to 24-7 psia 0 psig is equivalent to 14.7 psia.
Vacuum
Vacuum pressure is a single pressure measurement, which also has a reference to atmospheric pressure. Vacuum pressure is the measure of the depression of process pressure below atmospheric pressure. Vacuum pressure is generally measured in cm or inches of H20. For example, 14.7 psia is equivalent to 407.5 inches of H20. Therefore, a pressure of 10 inches of H20 vacuum implies process pressure is depressed 10 inches below atmosphere. Or 10 inches of H20 vacuum is equivalent to 397.5 inches of H20 absolute. Vacuum pressure is typically measured using a gauge pressure transmitter with an elevated zero calibration.
Classic pressure measurement devices
Most pressure-measurement devices belong to the manometers or to the elastic pressure sensors category. Manometers use a column of liquid to measure the pressure. The manometer mechanism applies the measured pressure to a column of liquid and the variation in the liquid level is measured. The use of a column of liquid limits the use of manometers to small near-atmospheric pressure. Piezometer tubes, U-tube manometers, and inclined-tube manometers are examples of simple manometers.
Elastic pressure sensors use an elastic element to measure pressure. The measured pressure pushes on an elastic element and the resulting deformation enables production of a signal proportional to the pressure. Most of the time, primary sensing elements in local indicators or in electronic transmitters are elastic pressure sensors. Bourdon tubes, strain gauges, diaphragms, and bellows meters are elastic pressure sensors. The sections below present the working principles of liquid manometers and Bourdon-tube pressure gauges. These devices are classic pressure measurement devices and understanding how they work will help your comprehension of the physics behind pressure measurement devices. The Discussion section of Ex. 3-1 thoroughly describes strain gauges, which are a type of elastic pressure sensor.
U-tube manometers
U-tube manometers are one of the oldest and simplest pressure-measurement devices. The main element of U-tube manometers is a U-shaped glass or plastic tube that contains a liquid such as water or mercury. The liquid is selected so that it does not react when in contact with the process fluid (Figure 3-11). One end of the tube is open to the atmosphere and the process fluid exerts a pressure at the other end of the tube. This pressure pushes the manometric liquid and causes it to rise in the tube proportionally. The height, or head, to which the manometric liquid rises above the point of contact with the process fluid, is proportional to the process fluid pressure. You can convert the height of liquid to a gauge pressure using Equation (3-8).
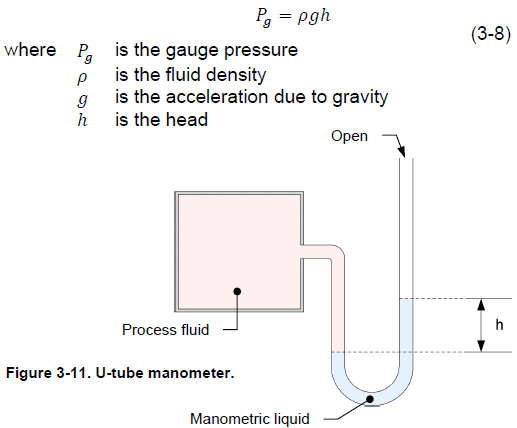
U-tube manometer manufacturers must select the manometric liquid with care so that it provides the desired measurement accuracy. The use of water manometers is limited to the measurement of pressure close to atmospheric pressure because a small variation in pressure causes a relatively large displacement of water. For example, to measure a gauge pressure of 7 kPa (1 psig) with a water manometer, the manometer column has to be over 71 cm (28 in) high. The manufacturer can significantly increase the measurement range of a manometer by using mercury instead of water. The density of mercury is 13.6 times the density of water. Thus, for a given pressure, the mercury displacement is 13.6 times less than the water displacement.
Liquid manometers are sufficiently accurate to serve as standards for checking the calibration of other pressure measurement devices. However, liquid manometers are fragile and bulky, which restricts their use to laboratories or as local indicators.
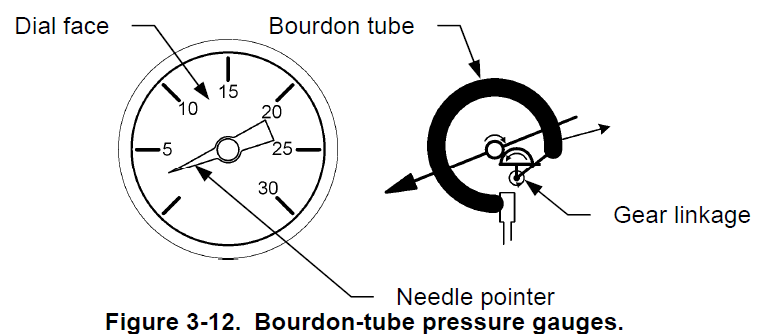
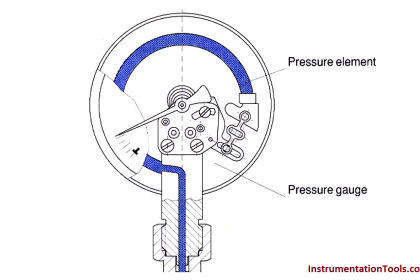
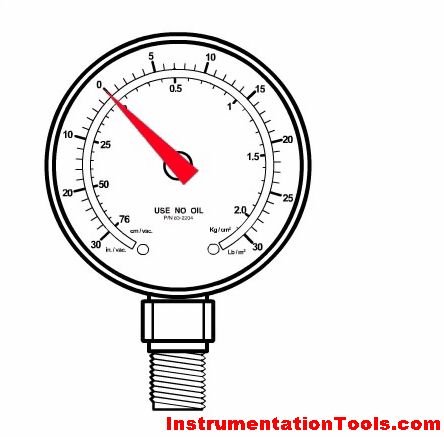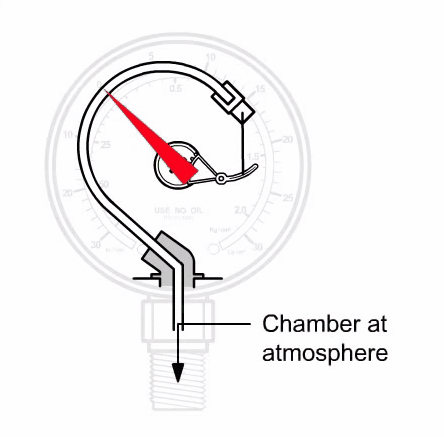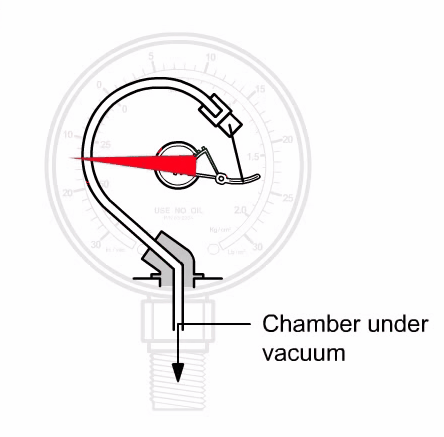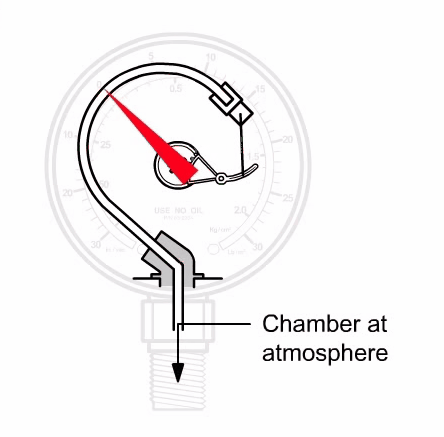
Bourdon tube pressure gauges
Bourdon-tube pressure gauges provide a direct reading of the pressure. They use a primary sensing element called a Bourdon tube to sense pressure. Figure 3-12 shows a typical bourdon-tube pressure gauge. The pressure gauge consists of a needle pointer attached through a gear linkage to a Bourdon tube, which is a C-shaped flexible coiled tube. The Bourdon tube is hollow and it connects directly into the process fluid line. As the pressure increases, the bourdon tube straightens which moves the gear linkage and causes the needle pointer to move on the dial. The Bourdon tube is made of material with elastic properties so that it deforms under pressure and returns to its original shape when it is no longer subject to pressure.
Also Read: Pressure Transmitter Working Animation











thanks very informative media