Feedforward Control with Dynamic Compensation

As we have discussed, feedforward control is a way to improve the stability of a feedback control system in the face of changing loads. Rather than rely on feedback to make corrective changes to a process only after some load change has driven the process variable away from setpoint, feedforward systems monitor the relevant load(s) and use that information to preemptively make stabilizing changes to the final control element such that the process variable will not be affected. In this way, the feedback loop’s role is to merely “trim” the process for factors lying outside the realm of the feedforward system.

At least, this is how feedforward control is supposed to work. One way feedforward controls commonly fail to live up to their promise is if the effects of load changes and of manipulated variable changes possess different time lags in their respective effects on the process variable. This is a problem in feedforward control systems because it means the corrective action called for in response to a change in load will not affect the process variable at the same time, or in the same way over time, as the load will. In order to correct this problem, we must intelligently insert time lags (or advancing time-based functions called leads) into the control system to equalize the time lags of load and feedforward correction. This is called dynamic compensation.

The following subsections will explore illustrative examples to make both the problem and the solution(s) clear.

A common area of confusion among students first approaching this topic is deciding where to place the dynamic compensation function in a feedforward control system. The answer to this question is surprisingly simple, although it may seem elusive at first glance. The key is found in the following principle: the only time-dynamic we have the ability to alter with our control system is the dynamic of the final control element. We cannot alter the time-dynamic of the load’s effect on the process variable, as that is strictly a function of process physics. Therefore, when we test a process employing feedforward control with an eye toward incorporating dynamic compensation, we must measure the time lag of the load’s effect on PV and also the time lag of our final control element’s effect on PV, then compare those two time lags. If the final control element’s time lag is shorter (quicker) than the load’s, then we must add a delay or lag to the feedforward signal so that the final control element’s preemptive action does not occur too soon. If the final control element’s time lag is longer (slower) than the load’s, then we must either find a way to alter the process itself to decrease the load’s time lag, or add a “lead” function to the feedforward signal in order to advance the final control element’s response and thereby ensure the preemptive action does not occur too late. Remember, all we can do with dynamic compensation is alter how the final control element responds (i.e. how slowly or quickly the preemptive action of feedforward occurs). The load’s effect on the process variable is fixed by the physics of the process and therefore lies beyond our direct control.

Dead time compensation

Examine the following control system P&ID showing the addition of flocculant (a chemical compound used in water treatment to help suspended solids clump together for easier removal by filtering and/or gravity clarification) and lime for pH balance. Flocculant is necessary to expedite the removal of impurities from the water, but some flocculation compounds have the unfortunate effect of decreasing the pH value of the water (turning it more acidic). If the water’s pH value is too low, the flocculant ironically loses its ability to function. Thus, lime (an alkaline substance – high pH value) must be added to the water to counter-act the flocculant’s effect on pH to ensure efficient flocculation. Both substances are powders in this water pre-treatment system, metered by variable-speed screw conveyors and carried to the mixing tank by belt-style conveyors:

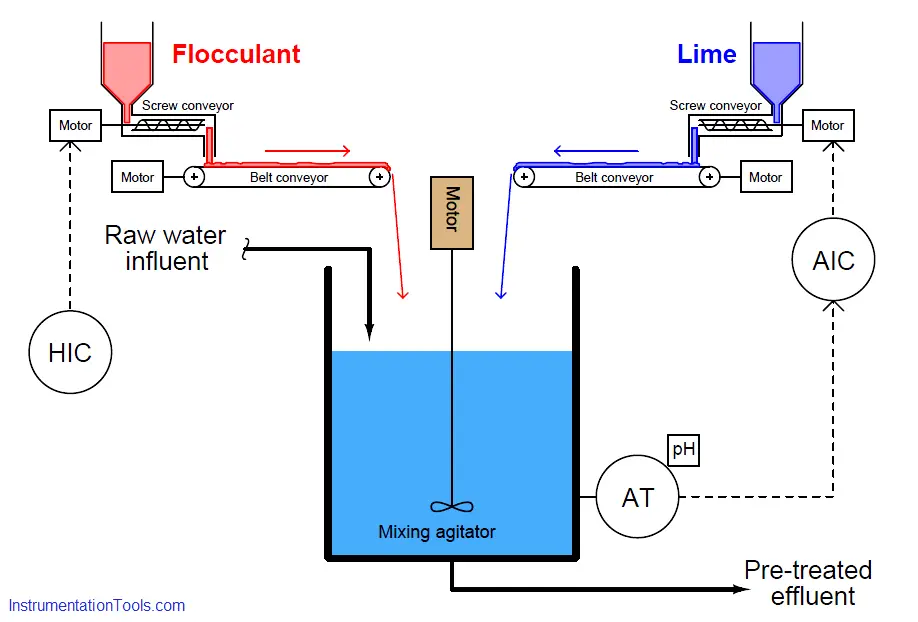
The control system shown in this P&ID consists of a pH analyzer (AT) transmitting a signal to a pH indicating controller (AIC), adjusting the speed of the lime screw conveyor. The flocculant screw conveyor speed is manually set by a hand indicating controller (HIC) – sometimes known as a manual loading station – adjusted when necessary by experienced water treatment operators who periodically monitor the effectiveness of flocculation in the system.

This simple feedback control system will work fine in steady-state conditions, but if the operator suddenly changes flocculant flow rate into the mixing vessel, there will be a temporary deviation of pH from setpoint before the pH controller is able to find the correct lime flow rate into the vessel to compensate for the change in flocculant flow. In other words, flocculant feed rate into the mixing tank is a load for which the pH control loop must compensate.

Dynamic response could be greatly improved with the addition of feedforward control to this system:

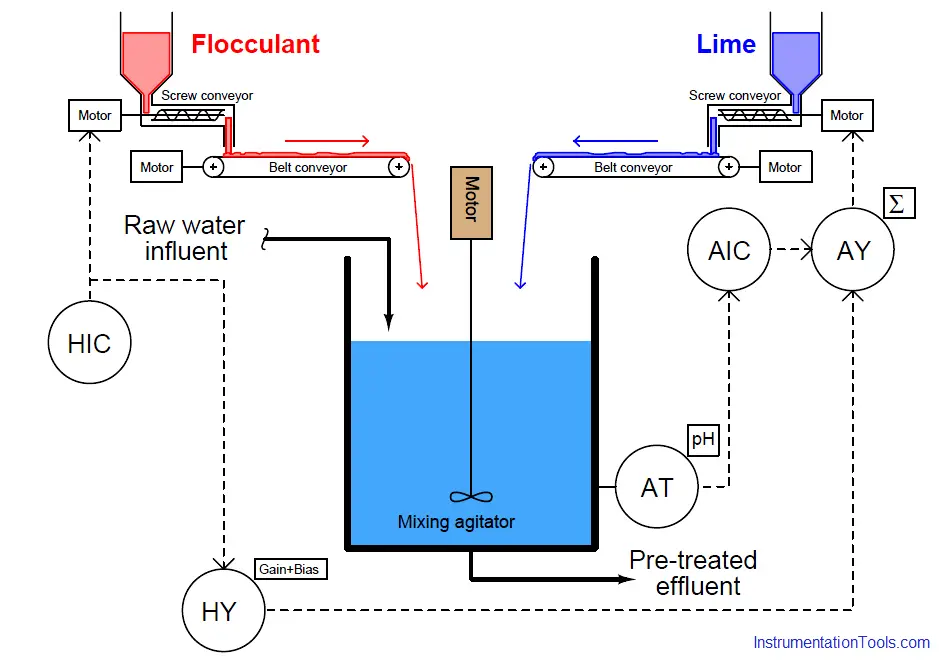
Here, the hand controller’s signal gets added to the pH controller’s output signal to directly influence lime feed rate in addition to acting as a control signal to the flocculant screw conveyor motor drive. If an operator changes the flocculant feed rate, the lime feed rate will immediately adjust to compensate, before any change in pH value takes place in the water. Ideally, the pH controller need only make minor “trim” adjustments to lime feed rate, while the feedforward signal does most of the work in maintaining a steady pH value. The proper proportioning and offset between flocculant and lime feed rates is established in the gain/bias function, which is “tuned” to ensure the feedforward signal does not over- or under-react, calling for too much (or too little) lime to compensate.

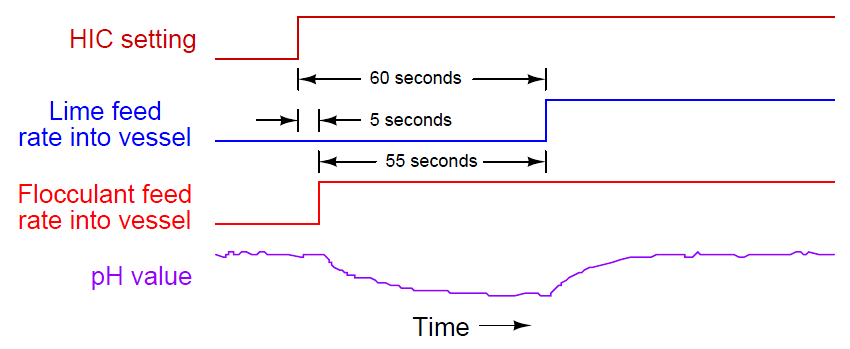
Even if all components in the feedforward system have been calibrated and configured properly, however, a potential problem still lurks in this system which can cause the pH value to temporarily deviate from setpoint following flocculant feed rate changes. This problem is the transport delay – otherwise known as dead time – inherent to the two belt conveyors transporting both flocculant and lime powder from their respective screw conveyors to the mixing vessel. If the rotational speed of a screw conveyor changes, the flow rate of powder exiting that screw conveyor will immediately and proportionately change. However, the belt conveyor imposes a time delay before the new powder feed rate enters the mixing vessel. In other words, the water in the vessel will not “see” the effects of a change in flocculant or lime feed rate until after the belt conveyor’s time delay has elapsed. This is not a problem if the dead times of both belt conveyors are exactly equal, since this means any compensatory change in lime feed rate initiated by the feedforward system will reach the water at exactly the same time the new flocculant rate reaches the water. So long as flocculant and lime feed rates are precisely balanced with one another at the point in time they reach the mixing vessel, pH should remain stable. But what if their arrival times are not coordinated – what will happen to pH then?

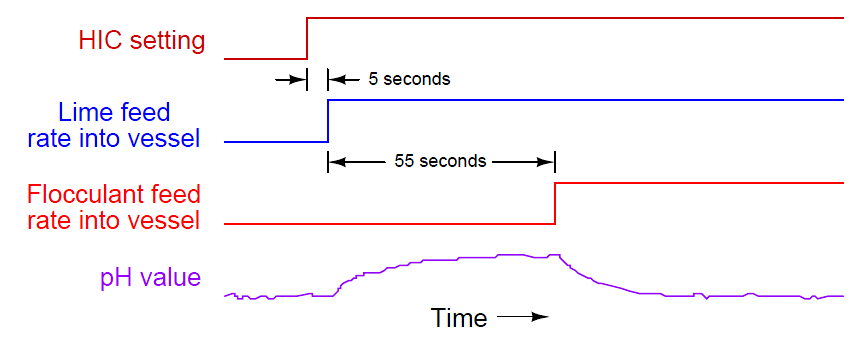
Let us engage in a “thought experiment” to explore the consequences of the flocculant conveyor belt moving much slower than, and/or being much longer than, the lime conveyor belt. Suppose the flocculant belt imposed a dead time of 60 seconds on flocculant powder making it to the vessel, while the lime belt only delayed lime powder transit by 5 seconds from screw conveyor to mixing tank. This would mean changes in flocculant flow (set by the hand controller) would compensate with changes in lime flow 55 seconds too soon. Now imagine the human operator making a sudden increase to the flocculant powder feed rate. The lime feed rate would immediately increase thanks to the efforts of the feedforward system. However, since the increased flow rate of lime powder will reach the mixing vessel 55 seconds before the increased flow rate of flocculant powder, the effect will be a temporary increase in pH value beginning about 5 seconds after the operator’s change, and then a settling of pH value back to setpoint, as shown in this timing diagram:

The obvious solution to this problem is to mechanically alter the belt conveyor systems for equal transport times of flocculant and lime powders. If this is impractical, we may achieve a similar result by incorporating another signal relay (or digital function block) inserting dead time into the feedforward control system. In other words, we can modify the control system in such a way to emulate what would be impractical to modify in the process itself.

This new function will add a dead time of 55 seconds to the feedforward signal before it enters the summer, thus delaying the lime feed rate’s response to feedforward effect by just the right amount of time such that any lime feed rate changes called for by feedforward action will arrive at the vessel simultaneously with the changed flocculant feed rate:

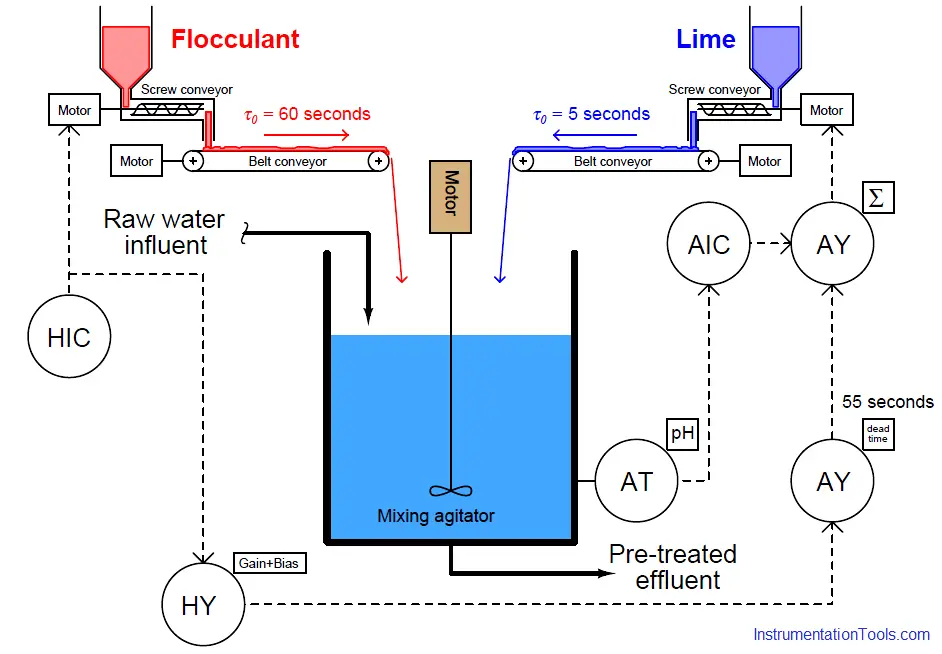
Adding time-based functions to a control system in order to equalize inherently unequal time delays in the physical process is called dynamic compensation. It is important to note that dynamic compensation cannot make physically unequal time lags equal – all it does is modify the feedforward system so that signal’s effect arrives at the right time to compensate the load. In simple terms, we can only use dynamic compensation to modify the FCE’s behavior, not the process behavior. Here, there is absolutely nothing the feedforward system can do to speed up the slower flocculant belt, so instead we chose to slow down the feedforward manipulation of lime flow to make it match the flocculant flow.

Note how the feedback pH controller’s loop was purposely spared the effects of the added dead time function, by placing the function outside of that controller’s feedback loop. This is important, as dead time in any form is the bane of feedback control. The more dead time within a feedback loop, the easier that loop will tend to oscillate. By strategically placing the dead time function before the summing relay rather than after (between the summer and the lime screw conveyor motor drive), the feedback control system still achieves minimum response time while only the feedforward signal gets delayed.

Let us now consider the same flocculant and lime powder control system, this time with transport delays reversed between the two belt conveyors. If the flocculant conveyor belt is now the fast one (5 seconds dead time) and the lime belt slow (60 seconds), the effects of flocculant feed rate changes will be reversed. An increase in flocculant powder feed rate to the vessel will result in a drop in pH beginning 5 seconds after the HIC setting change, followed by a rise in pH value after the additional lime feed rate finally reaches the vessel:

What is happening here is that the feedforward signal’s effect is coming too late. In a perfect world our lime flow rate into the mixing vessel should change at the same time that the flocculant flow rate changes. Instead, our lime flow rate’s necessary increase happens 55 seconds too late to prevent the pH from deviating.

It would be possible to compensate for the difference in conveyor belt transport times using a special relay in the same location of the feedforward signal path as before, if only there was such a thing as a relay that could predict the future exactly 55 seconds in advance!. Since no such device exists (or ever will exist), we must apply dynamic compensation elsewhere in the feedforward control system.

If a time delay is the only type of compensation function at our disposal, then the only thing we can delay in this system to make the two dead times equal is the flocculation feed rate. Thus, we should place a 55-second dead time relay in the signal path between the hand indicating controller (HIC) and the flocculant screw conveyor motor drive.

This diagram shows the proper placement of the dead time function: Motor

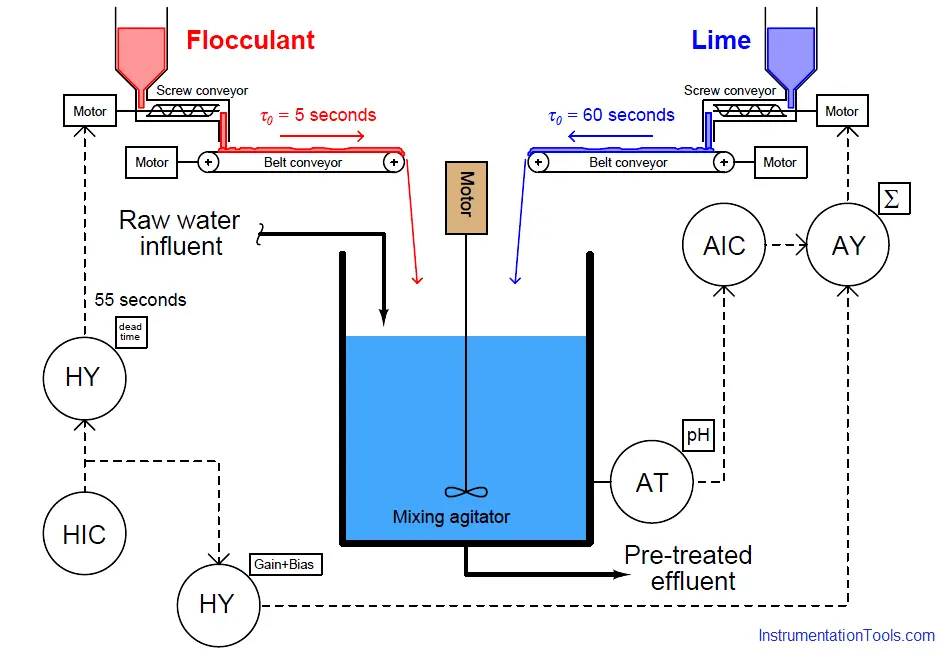
With this dead time relay in place, any change in flocculation feed rate initiated by a human operator will immediately adjust the feed rate of lime powder, but delay an adjustment to flocculant powder feed rate by 55 seconds, so the two powders’ feed rate changes arrive at the mixing vessel simultaneously.

Bear in mind that this solution will really only work in a system like this where the major load happens to be controlled by the human operator. In most processes the load variable is not under anyone’s control, making it difficult if not impossible to purposely delay its action. If the load has a shorter dead time than the compensation, there is usually little we can do within the control strategy to equalize those effects for better dynamic stability. Typically, the best solution is to physically alter the process (e.g. slow down the flocculant belt conveyor’s speed) so that the load and compensation dead times are closer to being equal.