Capacitors
The variation of an alternating voltage applied to a capacitor, the charge on the capacitor, and the current flowing through the capacitor are represented by Figure 3.
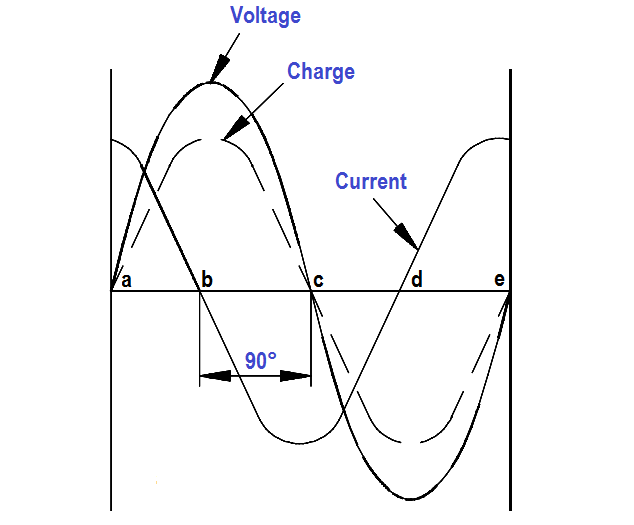
Figure 3 : Voltage, Charge, and Current in a Capacitor
The current flow in a circuit containing capacitance depends on the rate at which the voltage changes. The current flow in Figure 3 is greatest at points a, c, and e. At these points, the voltage is changing at its maximum rate (i.e., passing through zero).
Between points a and b, the voltage and charge are increasing, and the current flow is into the capacitor, but decreasing in value. At point b, the capacitor is fully charged, and the current is zero. From points b to c, the voltage and charge are decreasing as the capacitor discharges, and its current flows in a direction opposite to the voltage. From points c to d, the capacitor begins to charge in the opposite direction, and the voltage and current are again in the same direction.
At point d, the capacitor is fully charged, and the current flow is again zero. From points d to e, the capacitor discharges, and the flow of current is opposite to the voltage. Figure 3 shows the current leading the applied voltage by 90°. In any purely capacitive circuit, current leads applied voltage by 90°.
Capacitive Reactance
Capacitive reactance is the opposition by a capacitor or a capacitive circuit to the flow of current. The current flowing in a capacitive circuit is directly proportional to the capacitance and to the rate at which the applied voltage is changing. The rate at which the applied voltage is changing is determined by the frequency of the supply; therefore, if the frequency of the capacitance of a given circuit is increased, the current flow will increase.
It can also be said that if the frequency or capacitance is increased, the opposition to current flow decreases; therefore, capacitive reactance, which is the opposition to current flow, is inversely proportional to frequency and capacitance.
Capacitive reactance XC, is measured in ohms, as is inductive reactance.
The below Equation is a mathematical representation for capacitive reactance.
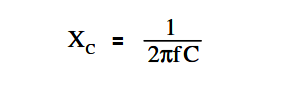
where
f = frequency (Hz)
π = ~3.14
C = capacitance (farads)
The below Equation is the mathematical representation of capacitive reactance when capacitance is expressed in microfarads (µF).
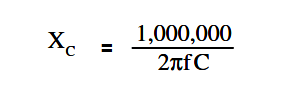
The below Equation is the mathematical representation for the current that flows in a circuit with only capacitive reactance.
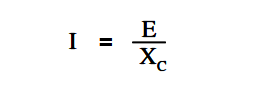
where
I = effective current (A)
E = effective voltage across the capacitive reactance (V)
XC = capacitive reactance (Ω)
Example:
A 10µF capacitor is connected to a 120V, 60Hz power source (see Figure 4). Find the capacitive reactance and the current flowing in the circuit. Draw the phasor diagram.
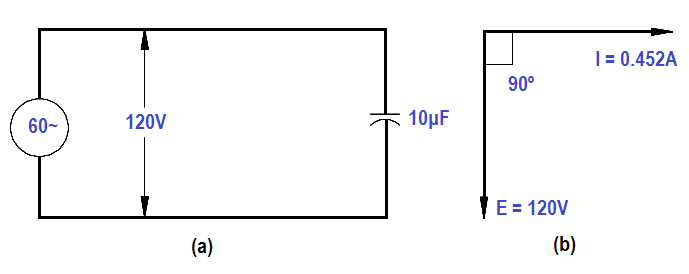
Figure 4 : Circuit and Phasor Diagram
Solution:
1. Capacitive reactance
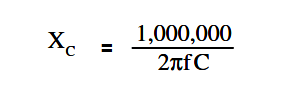
XC = 1,000,000 / [ (2)(3.14)(60)(10) ]
XC = 1,000,000 / 3768 = 265.4 Ω
2. Current flowing in the circuit
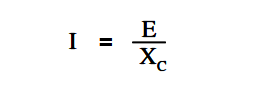
I = 120 / 265.4 = 0.452 amps
3. Phasor diagram showing current leading voltage by 90° is drawn in Figure 4b.