Series Resistance

The total resistance in a series circuit is equal to the sum of all the parts of that circuit, as shown in below equation.

R_T =R1 +R2 +R3 …      etc.

where
R_T = resistance total
R1 ,R2 , and R3 = resistance in series

Example:

A series circuit has a 60Ω, a 100Ω, and a 150Ω resistor in series (Figure 18). What is the total resistance of the circuit?

Figure 18 Resistance in a Series Circuit

Solution:

RT =R1 +R2 +R3

RT = 60 + 100 + 150

RT = 310 Ω

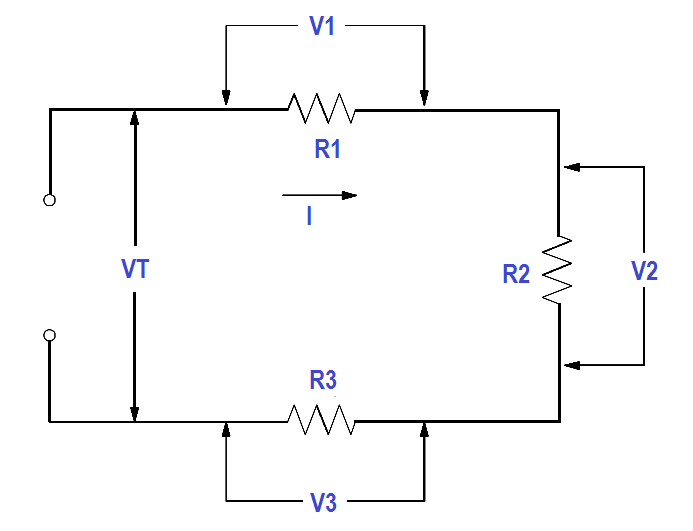
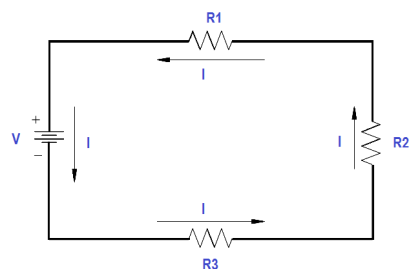
The total voltage across a series circuit is equal to the sum of the voltages across each resistor in the circuit (Figure 19) as shown in below equation.

VT =V1 +V2 +V 3 …     etc.

where

VT = total voltage

V1 = voltage across R1

V2 = voltage across R2

V3 = voltage across R3

Figure 19 Voltage Drops in a Series Circuit

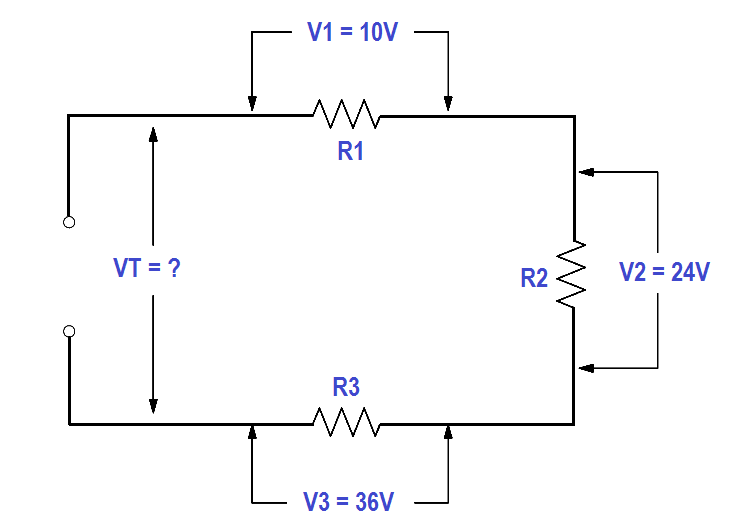
Ohm’s law may now be applied to the entire series circuit or to individual component parts of the circuit. When used on individual component parts, the voltage across that part is equal to the current times the resistance of that part. For the circuit shown in Figure 20, the voltage can be determined as shown below.

V1= IR1
V2 = IR2
V3 = IR3

VT = V1 + V2 + V3

VT = 10 volts + 24 volts + 36 volts
VT = 70 volts

Figure 20 Voltage Total in a Series Circuit

To find the total voltage across a series circuit, multiply the current by the total resistance as shown in below equation.

V_T = I . R_T

where

VT = total voltage
I = current
R_T = total resistance

Example 1:

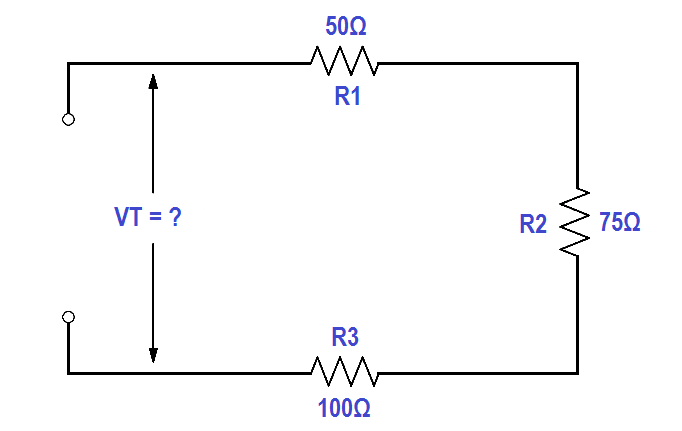
A series circuit has a 50Ω, a 75Ω, and a 100Ω resistor in series (Figure 21). Find the voltage necessary to produce a current of 0.5 amps.

Figure 21 Example 1 Series Circuit

Solution:

Step 1: Find circuit current. As we already know, current is the same throughout a series circuit, which is already given as 0.5 amps.

Step 2: Find R_T

RT = R1 + R2 + R3

RT = 50 Ω + 75 Ω + 100 Ω

RT = 225 Ω

Step 3: Find VT .

Use Ohm’s law. V_T = I . R_T

VT = 0.5 x 225

VT = 112.5 volts

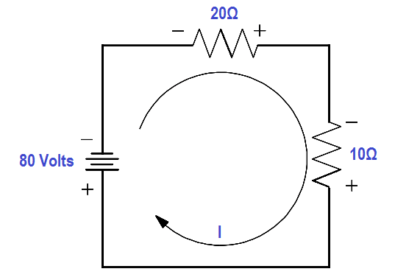
Example 2:

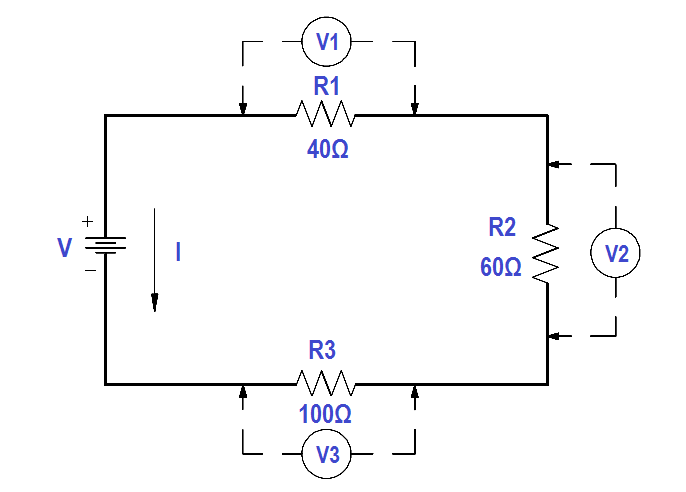
A 120 V battery is connected in series with three resistors: 40Ω, 60Ω, and 100Ω (Figure 22). Find the voltage across each resistor.

Figure 22 Example 2 Series Circuit

Solution:

Step 1: Find total resistance.

RT = R1 + R2 + R3

RT = 40 Ω + 60 Ω + 100 Ω

RT = 200 Ω

Step 2: Find Circuit Current (I) .

Use Ohm’s law. V_T = I . R_T

Solving for I

I = V_T/R_T

I = 120/200 = 0.6 amps

Step 3: Find the voltage across each component.

V1= IR1
V1 = (0.6 amps)(40 Ω)
V1 = 24 volts

V2 = IR2
V2 = (0.6 amps)(60 Ω)
V2 = 36 volts

V3 = IR3
V3 = (0.6 amps)(100 Ω)
V3 = 60 volts

The voltages of V1 ,V2 , and V3 in Example 2 are known as “voltage drops” or “IR drops.” Their effect is to reduce the available voltage to be applied across the other circuit components. The sum of the voltage drops in any series circuit is always equal to the applied voltage. We can verify our answer in Example 2 by using below equation

VT = V1 + V2 + V3

120 volts = 24 volts + 36 volts + 60 volts

120 volts = 120 volts