In 1827 the German physicist George Ohm published a pamphlet entitled “The Galvanic Circuit Investigated Mathematically”. It contained one of the first efforts to measure currents and voltages and to describe and relate them mathematically. One result was a statement of the fundamental relationship we now call Ohm’s Law.
Consider a uniform cylinder of conducting material, to which a voltage has been connected. The voltage will cause charge to flow, i.e. a current:
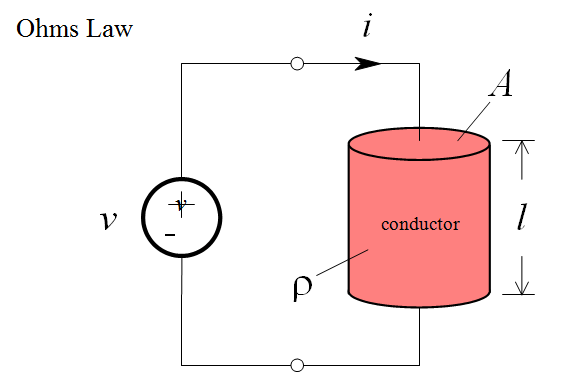
Ohm found that in many conducting materials, such as metal, the current is always proportional to the voltage. Since voltage and current are directly proportional, there exists a proportionality constant R, called resistance, such that:
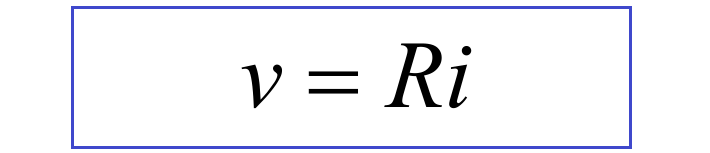
This is Ohm’s Law. The unit of resistance (volts per ampere) is referred to as the ohm, and is denoted by the capital Greek letter omega, Ω.
We refer to a construction in which Ohm’s Law is obeyed as a resistor.
The ideal resistor relationship is a straight line through the origin:
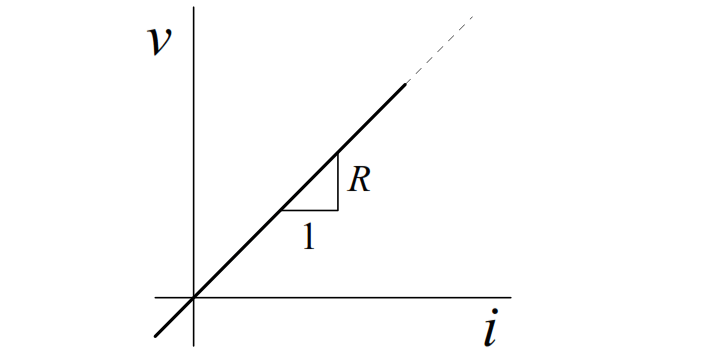
Even though resistance is defined as R = v/i , it should be noted that R is a purely geometric property, and depends only on the conductor shape and the material used in the construction. For example, it can be shown for a uniform resistor that the resistance is given by:
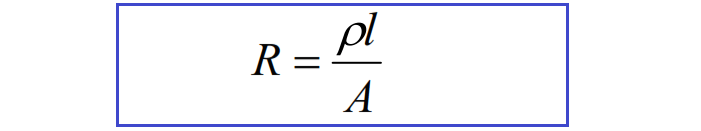
where l is the length of the resistor, and A is the cross-sectional area. The resistivity, r , is a constant of the conducting material used to make the resistor.
The circuit symbol for the resistor is shown below, together with the direction of current and polarity of voltage that make Ohm’s Law algebraically correct:
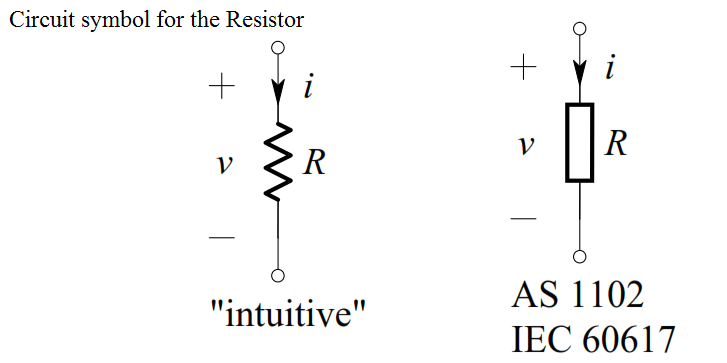
Example
Consider the circuit shown below.
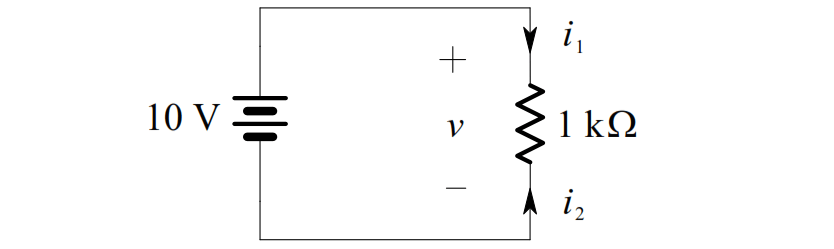
The voltage across the 1 kΩ resistor is, by definition of an ideal voltage source,
v(t ) = 10 V . Thus, by Ohm’s Law, we get:
i1 = v/R = 10/1000 = 0.01 A = 10 mA
i2 = –v/R = -10/1000 = -0.01 A = -10 mA
Note that i2 = –i1 , as expected


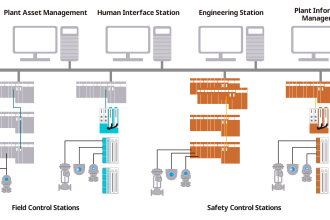

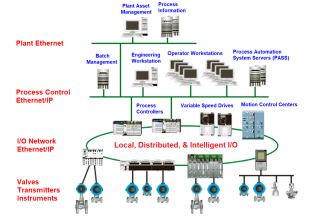


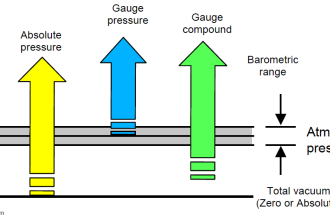
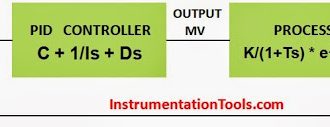

Very interesting and helpful.
Young and upcoming engineers should take note