Kirchhoff’s first law is also known as his “voltage law.” The voltage law gives the relationship between the “voltage drops” around any closed loop in a circuit, and the voltage sources in that loop. The total of these two quantities is always equal.
In equation form:
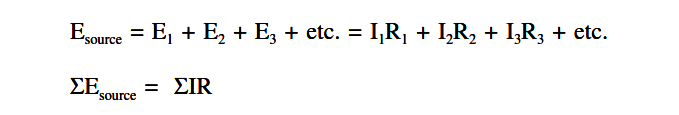
where the symbol Σ (the Greek letter sigma) means “the sum of.”
Kirchhoff’s voltage law can be applied only to closed loops (Figure 32). A closed loop must meet two conditions:
- It must have one or more voltage sources.
- It must have a complete path for current flow from any point, around the loop, and back to that point.

Figure 32 Closed Loop
You will remember that in a simple series circuit, the sum of the voltage drops around the circuit is equal to the applied voltage. Actually, this is Kirchhoff’s voltage law applied to the simplest case, that is, where there is only one loop and one voltage source.
Applying Kirchhoff’s Voltage Law
For a simple series circuit, Kirchhoff’s voltage law corresponds to Ohm’s Law. To find the current in a circuit (Figure 33) by using Kirchhoff’s voltage law, use below equation.
ΣEsource = Σ I R
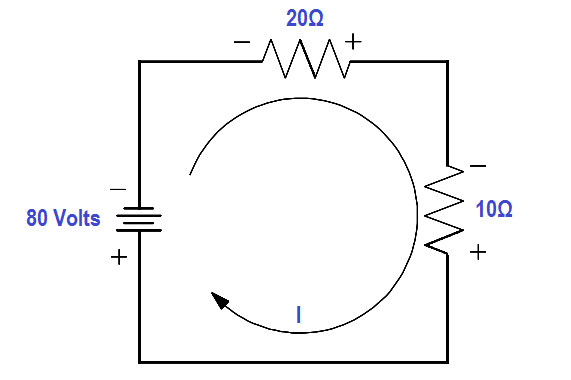
Figure 33 Using Kirchhoff’s Voltage Law to find Current with one Source
80 = 20 (I) + 10 (I)
80 = 30 (I)
I = 80/30 = 2.66 amps
In the problem above, the direction of current flow was known before solving the problem. When there is more than one voltage source, the direction of current flow may or may not be known. In such a case, a direction of current flow must be assumed in the beginning of the problem.
All the sources that would aid the current in the assumed direction of current flow are then positive, and all that would oppose current flow are negative. If the assumed direction is correct, the answer will be positive. The answer would be negative if the direction assumed was wrong. In any case, the correct magnitude will be attained.
For example, what is the current flow in Figure 34? Assume that the current is flowing in the direction shown.
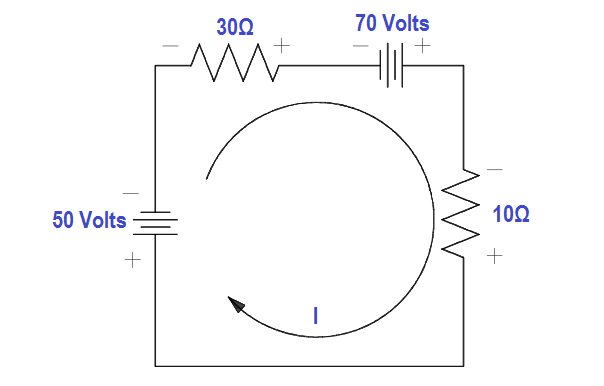
Figure 34 Using Kirchhoff’s Voltage Law to find Current with Multiple Battery Sources
Using Kirchhoff’s Voltage Law:
ΣEsource = Σ I R
50 – 70 = 30I + 10I
-20 = 40I
I = -20/40 = -0.5
The result is negative. The current is actually 0.5 ampere in the opposite direction to that of the assumed direction.