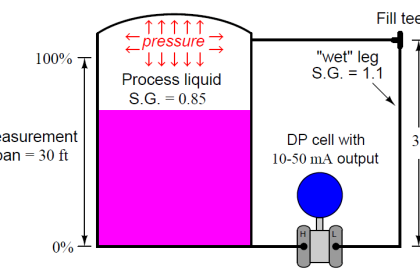
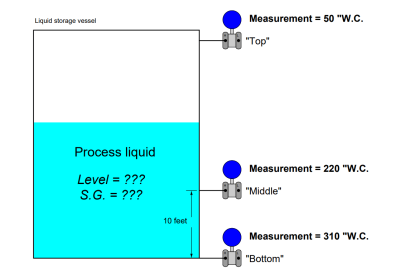
Specific gravity is defined as the ratio of densities between a particular fluid and a reference fluid. For liquids, the reference fluid is water; for gases, the reference fluid is air.
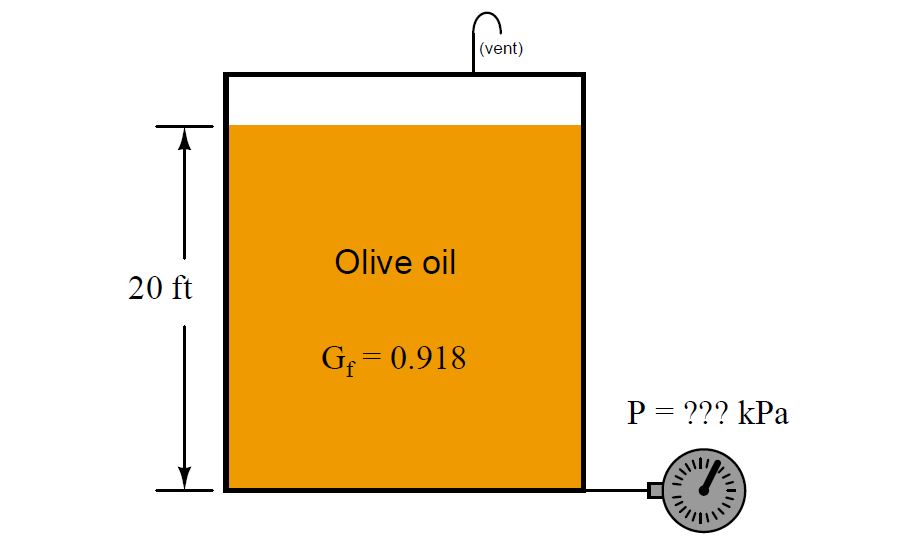
For example, the density of olive oil is 57.3 lb/ft3 and the density of water is 62.4 lb/ft3. Calculating the ratio of these two densities yields the specific gravity of olive oil: 0.918. That is to say, the density of olive oil is 91.8% that of water.
A useful definition of specific gravity when performing hydrostatic pressure calculations for various liquids is the ratio of equivalent water column height to the height of a particular liquid. Using the specific gravity of olive oil (0.918) as an example, we could say that 0.918 units of water column height will generate the same hydrostatic pressure as 1 unit of olive oil height.
The unit could be “inches,” “centimeters,” “millimeters,” “cubits,” or anything else: 0.918 unit W.C. pressure = 1 unit olive oil pressure We may make a “unity fraction” from this equality, since we are dealing with two physically equal quantities: the amount of hydrostatic pressure generated by two vertical columns of different liquids.
(0.918 unit W.C.) / 1 unit olive oil) = unity
Apply this “unity fraction” to the calculation of hydrostatic pressure at the bottom of a 20 foot tall storage tank filled to the top with olive oil, expressing that pressure in units of kPa. Show how the units cancel in your calculation(s), beginning with feet of olive oil and ending in kilo-Pascals (kPa):
Answer
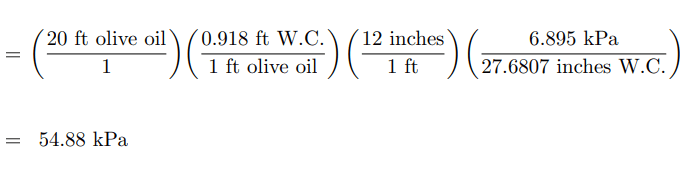Share your answers with us through the below comments section.
Read Next:
- Motion-Balance Instrument
- PLC Pneumatic Circuit
- PSV Lift Pressure
- Air Compressor Problem
- DP Transmitter Pressure
Credits: Tony R. Kuphaldt