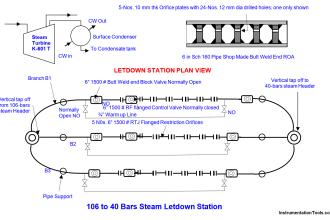
The Law of Continuity for fluids states that the product of mass density (ρ), cross-sectional pipe area (A) and average velocity (v) must remain constant through any continuous length of pipe:
Velocity-based flow meters
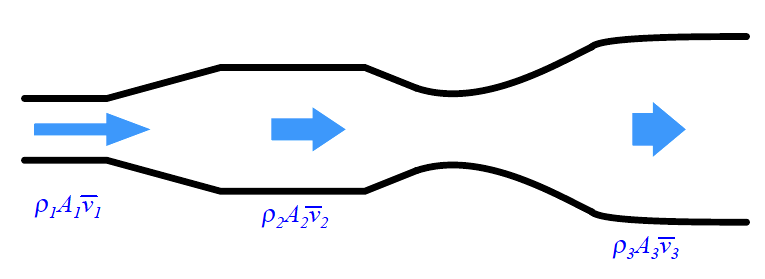
If the density of the fluid is not subject to change as it travels through the pipe (a very good assumption for liquids), we may simplify the Law of Continuity by eliminating the density terms from the equation:
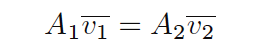
The product of cross-sectional pipe area and average fluid velocity is the volumetric flow rate of the fluid through the pipe (Q = Av).
This tells us that fluid velocity will be directly proportional to the volumetric flow rate given a known cross-sectional area and a constant density for the fluid flow stream.
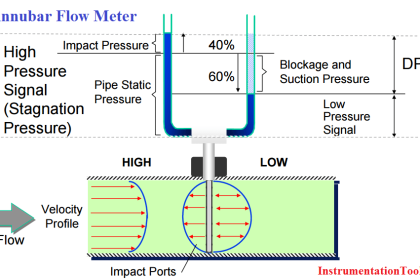
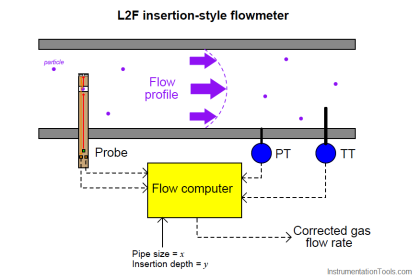
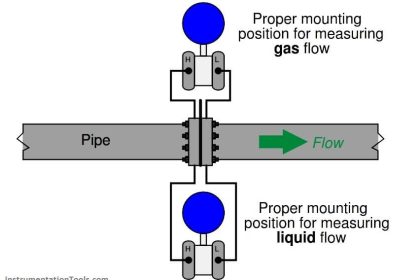
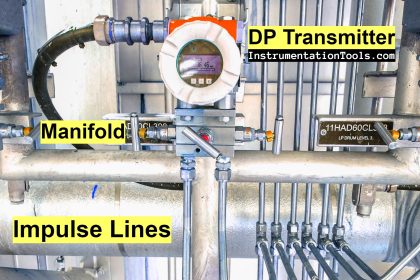
Any device able to directly measure fluid velocity is therefore capable of inferring the volumetric flow rate of fluid in a pipe. This is the basis for velocity-based flow meter designs.
Example Flow Meters