The inverse z-transform & Response of Linear Discrete Systems
1. Unit step response of the system described by the equation y(n) +y(n-1) =x(n) is:
a) z2/(z+1)(z-1)
b) z/(z+1)(z-1)
c) z+1/z-1
d) z(z-1)/z+1
Answer: a
Explanation: Response of the system is calculated by taking the z-transform of the equation and input to the transfer function in the step input.
2. Inverse z-transform of the system can be calculated using:
a) Partial fraction method
b) Long division method
c) Basic formula of the z-transform
d) All of the mentioned
Answer: d
Explanation: Inverse z-transform is the opposite method of converting the transfer function in Z domain to the discrete time domain and this can be calculated using all the above formulas.
3. Assertion (A): The system function
H(z) = z3-2z2+z/z2+1/4z+1/s is not causal
Reason (R): If the numerator of H (z) is of lower order than the denominator, the system may be causal.
a) Both A and R are true and R is correct explanation of A
b) Both A and R are true and R is not correct Explanation of A
c) A is True and R is false
d) A is False and R is true
Answer: a
Explanation: The transfer function is not causal as for causality the numerator of H (z) is of lower order than the denominator, the system may be causal.
4. Assertion (A): Z-transform is used to analyze discrete time systems and it is also called pulsed transfer function approach.
Reason(R): The sampled signal is assumed to be a train of impulses whose strengths, or areas, are equal to the continuous time signal at the sampling instants.
a) Both A and R are true and R is correct explanation of A
b) Both A and R are true and R is not correct Explanation of A
c) A is True and R is false
d) A is False and R is true
Answer: a
Explanation: Z-transform is used to convert the discrete time systems into the z domain and it is also called pulsed transfer function approach that is justified only at the sampling instants.
5. The z-transform corresponding to the Laplace transform G(s) =10/s(s+5) is
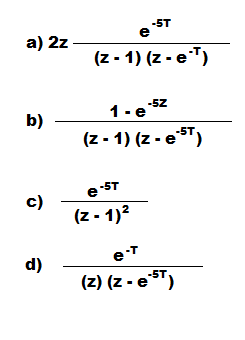
Answer: b
Explanation: Laplace transform is the technique of relating continuous time to the frequency domain while the z transform is relating discrete time hence Laplace transform is first converted into time domain and then the z transform is calculated.
6. Homogeneous solution of: y(n) -9/16y(n-2) = x(n-1)
a) C1(3/4)n+C2(3/4)-n
b) C1-(3/4)n-1+C2(3/4)n-1
c) C1(3/4)n
d) C1-(3/4)n
Answer: a
Explanation: Taking the z-transform of the given difference equation and solving the homogeneous equation and finding the solution using complimentary function.
7. If the z transform of x(n) is X(z) =z(8z-7)/4z2-7z+3, then the final value theorem is :
a) 1
b) 2
c) ∞
d) 0
Answer: a
Explanation: Final value theorem is calculated for the transfer function by equating the value of z as 1 and this can be calculated only for stable systems.
8. Final value theorem is used for:
a) All type of systems
b) Stable systems
c) Unstable systems
d) Marginally stable systems
Answer: b
Explanation: Final value theorem is used to calculate the final value as for time infinite and for z = 1 the final value theorem can be calculated and final value theorem is for for stable systems.
9. If the z-transform of the system is given by H (z) = a+z-1/1+az-1 . Where a is real valued:
a) A low pass filter
b) A high pass filter
c) An all pass filter
d) A bandpass filter
Answer: c
Explanation: The discrete time frequency response will be aperiodic and does not depend on the frequency and the transfer function will be representing the all pass filter.
10. The system is stable if the pole of the z-transform lies inside the unit circle
a) True
b) False
Answer: a
Explanation: For the system to be stable in Z domain the pole in the this domain must lie inside the unit circle and for the causal stable region must be outside the circle and hence the locus will be a ring.