The Z-Transform
1. The discrete-time signal x (n) = (-1)n is periodic with fundamental period
a) 6
b) 4
c) 2
d) 0
Answer: c
Explanation: Period of the signal refers to the instant of time at which the signal repeats itself and for this Period =2 of the given discrete time signal.
2. The frequency of a continuous time signal x (t) changes on transformation from x (t) to x (α t), α > 0 by a factor
a) α
b) 1/α
c) α2
d) α
Answer: a
Explanation: x(t)->x(αt), α > 0
α > 1 compression in t, expansion in f by α.
α < 1 expansion in t, compression in f by α.
3. Two sequences x1 (n) and x2 (n) are related by x2 (n) = x1 (- n). In the z- domain, their ROC’s are
a) The same
b) Reciprocal of each other
c) Negative of each other
d) Complements of each other
Answer: b
Explanation: x1(n) is the signal in the discrete domain and X1(z) is the signal in the z domain, RoC Rx
z Reciprocals x2(n) = x1(-n) X1(1/z), RoC 1/ Rx
4. The ROC of z-transform of the discrete time sequence x(n) =
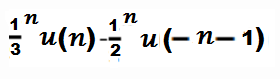
is:
a) 1/3>|z|<1/2
b) |z|>1/2
c) |z|<1/3
d) 2>|z|<3
Answer: a
Explanation: One part of the equation is the right sided signal and other part is the left sided signal hence the ROC of the system will be 1/3>|z|<1/2.
5. Which one of the following is the correct statement? The region of convergence of z-transform of x[n] consists of the values of z for which x[n] is:
a) Absolutely integrable
b) Absolutely summable
c) Unity
d) <1
Answer: b
Explanation: The region of convergence of z-transform of x[n] consists of the values of z for which x[n]r-n is absolutely summable.
6. The region of convergence of the z-transform of a unit step function is:
a) |z|>1
b) |z|<1
c) (Real part of z)>0
d) (Real part of z)<0
Answer: a
Explanation: h[n] =u[n] Hence, Region of Convergence is the region for which the values of the roots in z transform are lying in the function and is the range of values of z for which |z|>1.
7. If the region of convergence of x1[n]+x2[n] is 1/>|z|<2/3, the region of convergence of x1[n]-x2[n] includes:
a) 1/3>|z|<3
b) 2/3>|z|<3
c) 3/2>|z|<3
d) 1/3>|z|<2/3
Answer: d
Explanation: Region of Convergence is the region for which the values of the roots in z transform are lying in the function and ROC remains the same for addition and subtraction in z-domain.
8. A sequence x (n) with the z-transform X (z) = Z4 + Z2 – 2z + 2 – 3Z-4 is applied to an input to a linear time invariant system with the impulse response h (n) = 2δ (n-3). The output at n = 4 will be:
a) -6
b) Zero
c) 2
d) -4
Answer: b
Explanation: H (z) = 2z-3
Then taking the inverse Laplace transform of the equation of Y (z) at n=4 y(n) =0.
9. H (z) is discrete rational transfer function. To ensure that both H(z) and its inverse are stable:
a) Poles must be inside the unit circle and zeros must be outside the unit circle
b) Poles and zeroes must be inside the unit circle
c) Poles and zeroes must be outside the unit circle
d) Poles must be outside the unit circle and zeros must be inside the unit circle
Answer: b
Explanation: For H(z) to be stable the poles must be inside the unit circle and for the inverse of H(z) to be stable the poles of it must be inside the unit circle.
10. Z and Laplace transform are related by:
a) s = ln z
b) s =ln z/T
c) s =z
d) s= T/ln z
Answer: b
Explanation: z = est
s =ln z/T.