Communication between InTouch Scada and Allen Bradley PLC

This article is about communication between InTouch SCADA and Allen Bradley PLC with a ladder logic example with screenshots.

InTouch Scada and Allen Bradley PLC

Do follow the below steps for establishing the communication process.

Step 1:

Open RSlogix software along with RSlinx and emulator.

Step 2:

Create a new project in RSlogix and established communication with an emulator.

Step 3:

Open InTouch SCADA software.

Step 4:

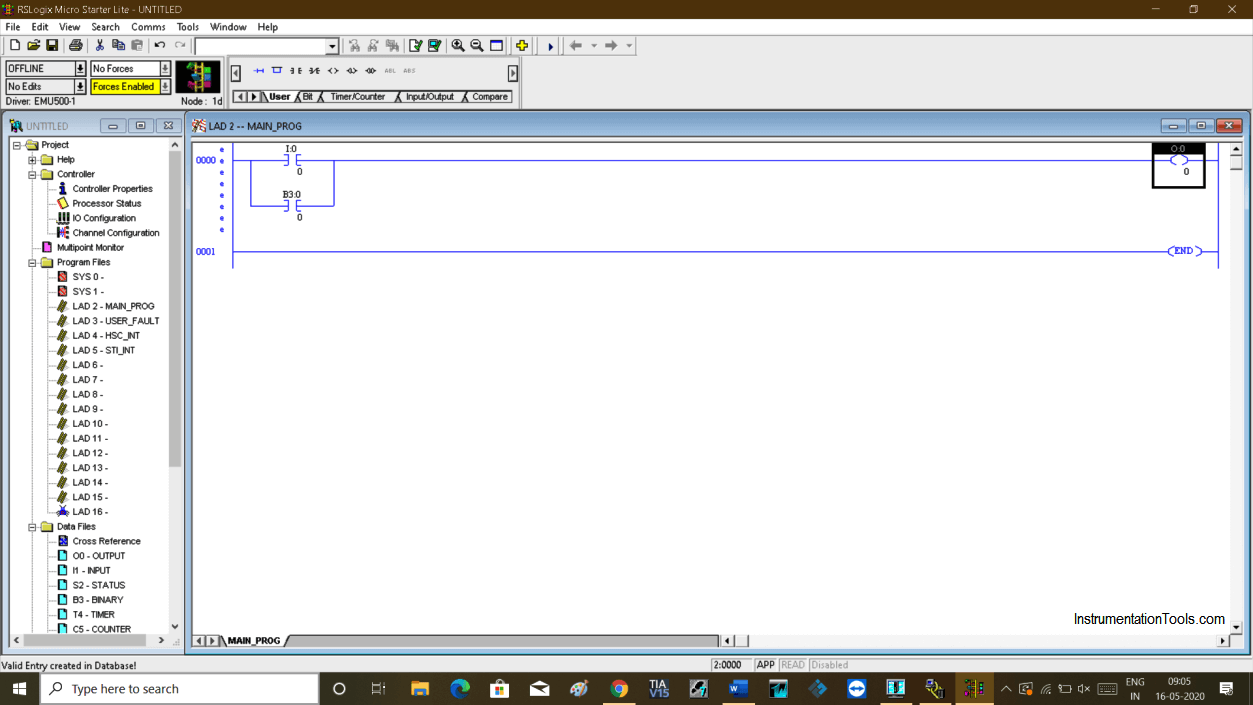
As you can see in the below window of RSlogix I have created a small example with one input and output.

In branch, I have use memory bit which we will use in SCADA to give a command.

Step 5:

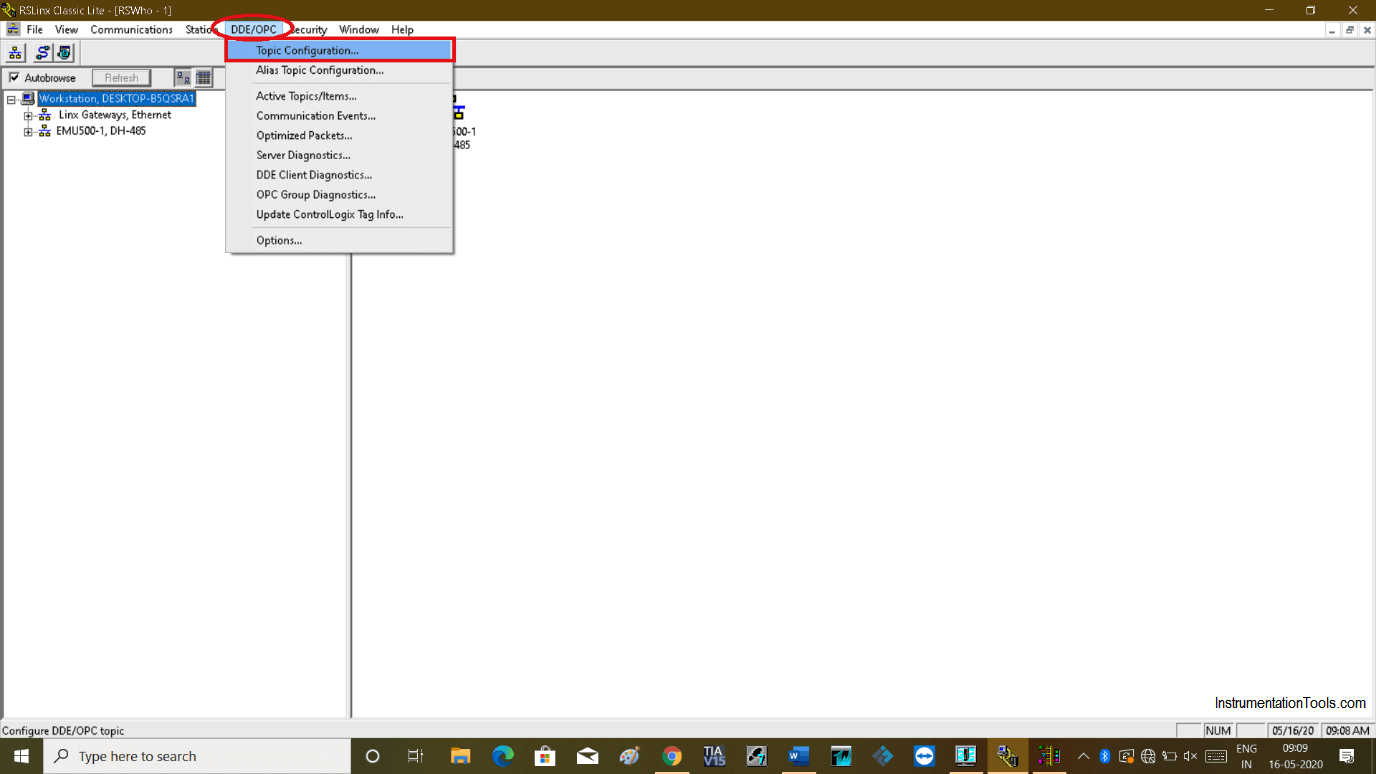
Now, let open RSlinx. Click on option “DDE/OPC” and choose “topic configuration”.

Step 6:

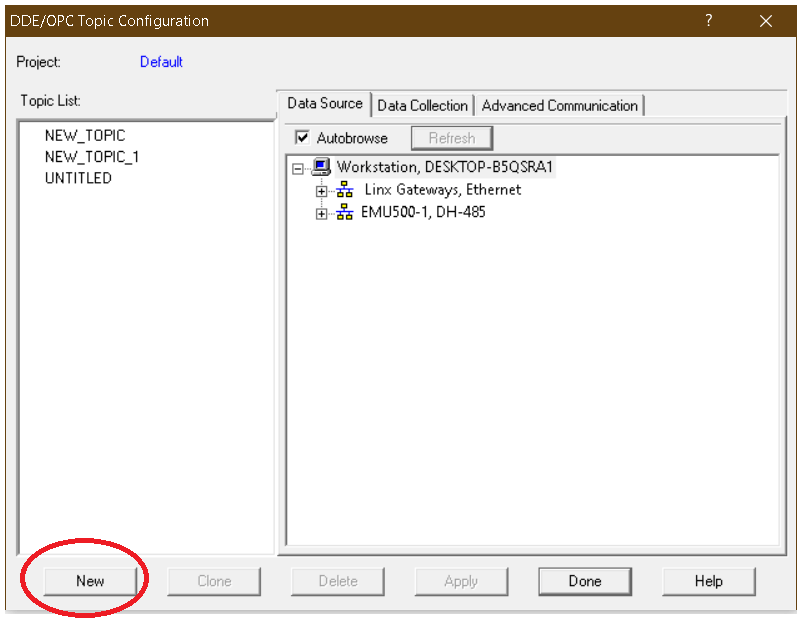
Following window will pop-up. Choose “New” to proceed.

Step 7:

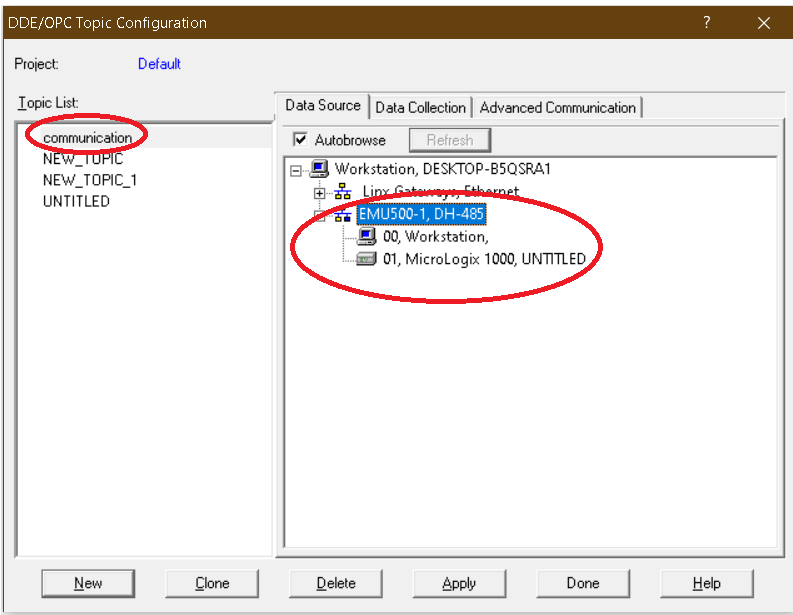
Create a new topic as I have created communication and choose communication protocol. Click “apply” then “done” to proceed.

Step 8:

Now open InTouch SCADA. Create a new project.

As we have used one input and output we have to create one input button and output button as shown in the below window.

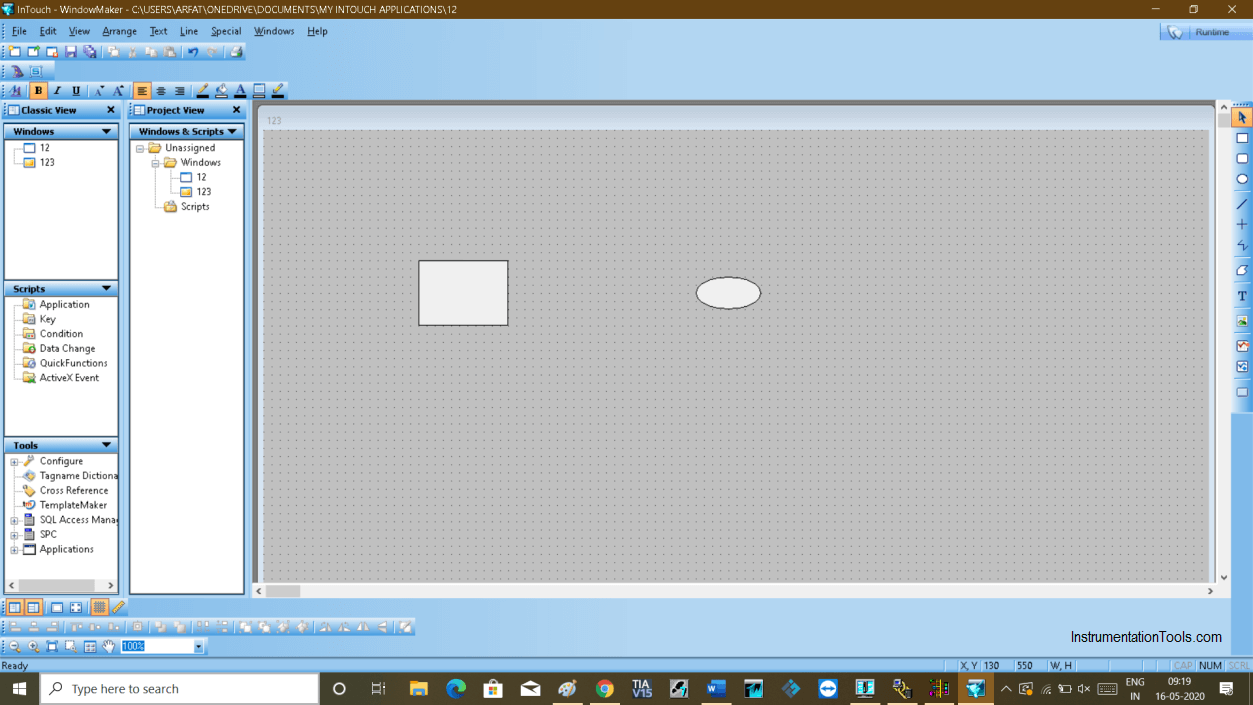
Step 9:

Hit double click on a button will open up the following window. Choose “Discrete” will open up a new window.

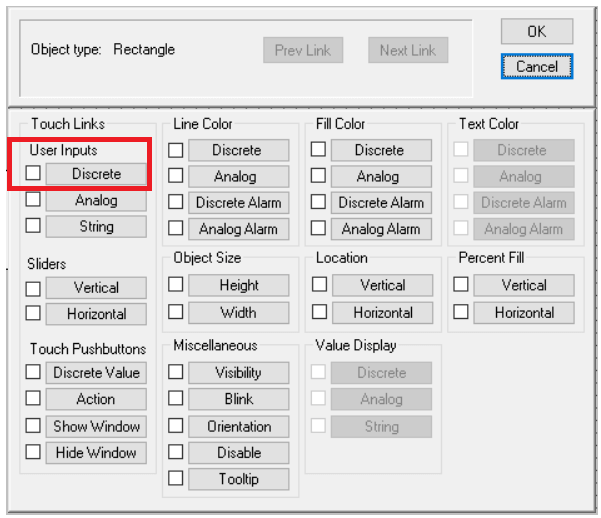
Step 10:

Give a name to button and hit “ok” to proceed.

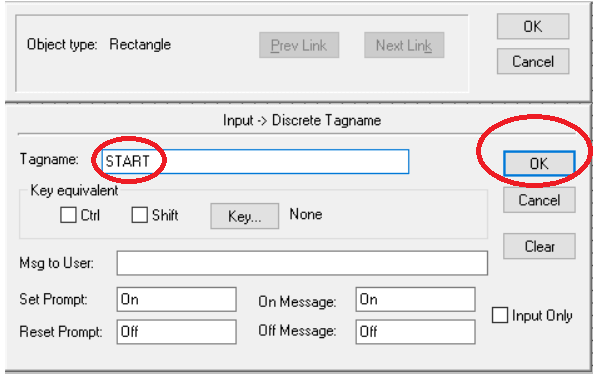
Step 11:

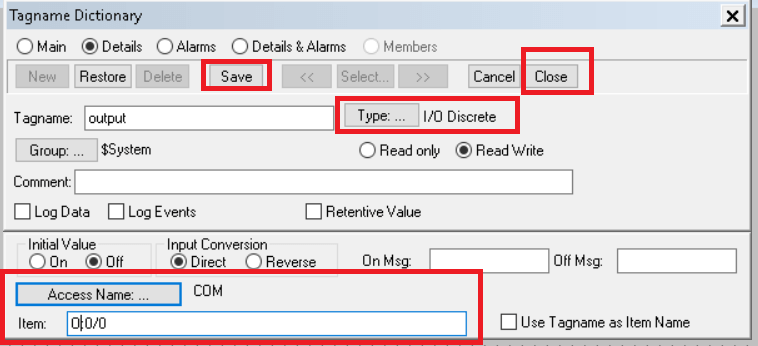
Choose I/O Discrete in the “Type” option. Then click on “access name”.

Write a bit address in “item” for input which we have used in the programming software (check step no. 4).

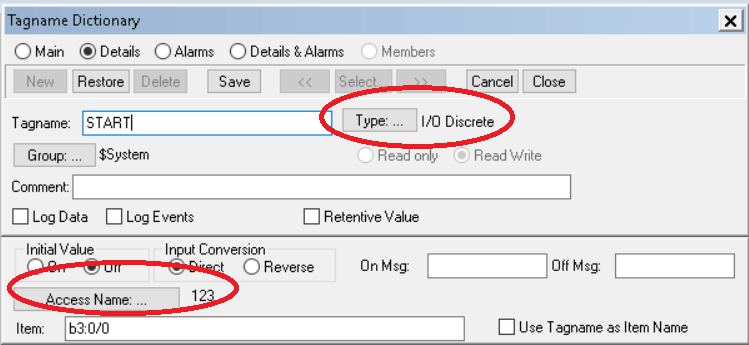
Step 12:

Clicking on Access name will open another window. Click on “add” as shown in the below window.

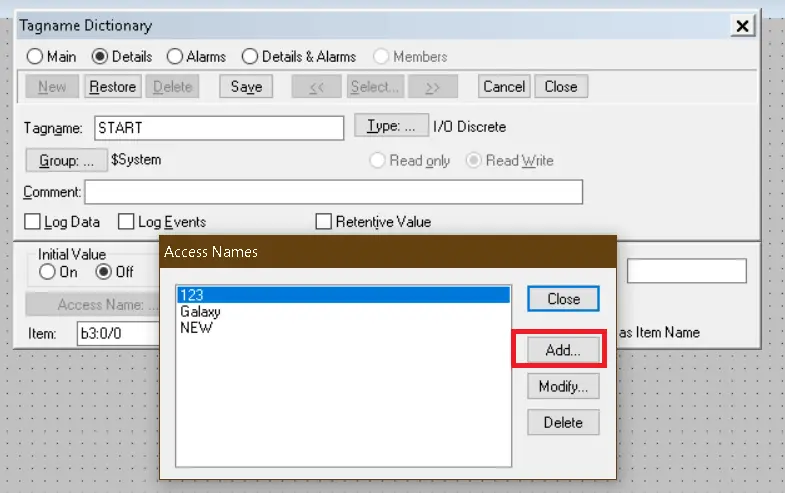
Step 13:

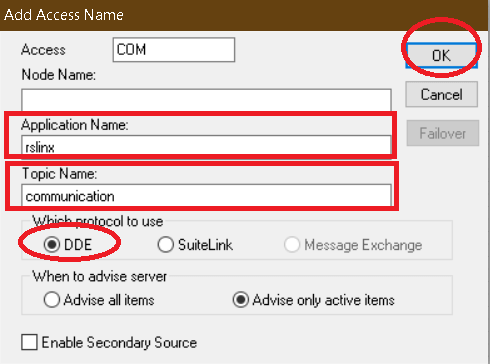
This is a very important step to establish communication.

Access: Give any name

Application name: RSlogix

Topic name: communication (the same name we have used in step no. 7)

Choose “DDE” as a communication protocol and hit “ok” to proceed.

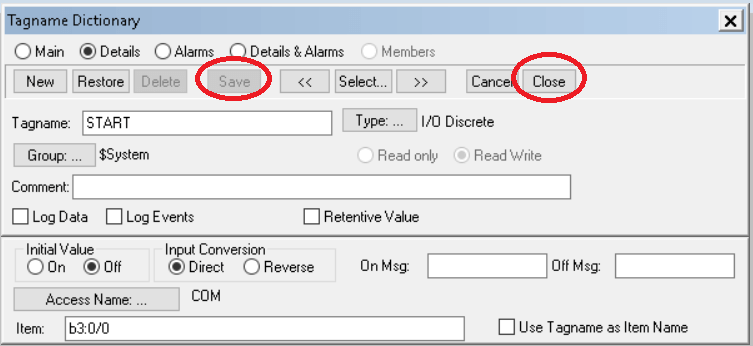
Step 14:

After configuration hit “save” and close the pop-up.

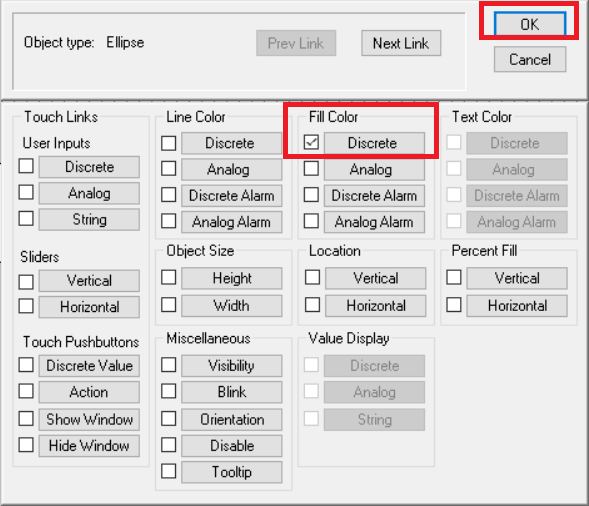
Step 15:

For output, we have select “fill color” property and choose “Discrete”.

Step 16:

Do follow the same procedure for output as shown in the below window.

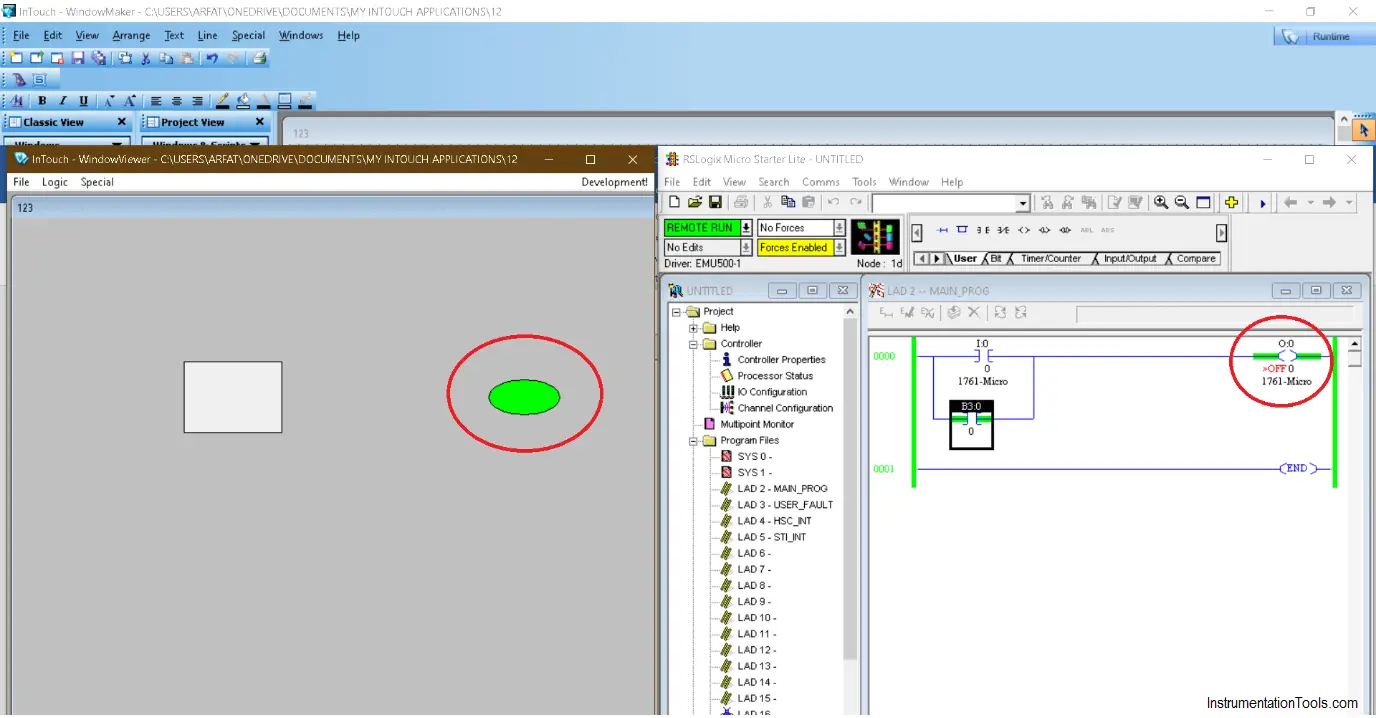
Step 17:

Communication has established. Test the logic. Keep a window in “runtime” and put CPU in “run” mode.

As you can see in the below window output gets energized if I give the command from SCADA.

Author: Suhel Patel

If you liked this article, then please subscribe to our YouTube Channel for PLC and SCADA video tutorials.

You can also follow us on Facebook and Twitter to receive daily updates.

Read Next:

• Quiz Questions on Motors
• Modifying PLC Programs
• Field instrument to Control Room
• What is SCADA System?
• Siemens Profinet Configuration