Displacer Level Measurement Calculations
Problem 1 :-
A steel displacer of volume 0.25 cubic feet is 50% immersed in oil of relative density 0.78;
the density of steel = 490 lbs per cubic foot
the density of water = 63 × lbs per cubic foot
Calculate the apparent weight of the displacer.
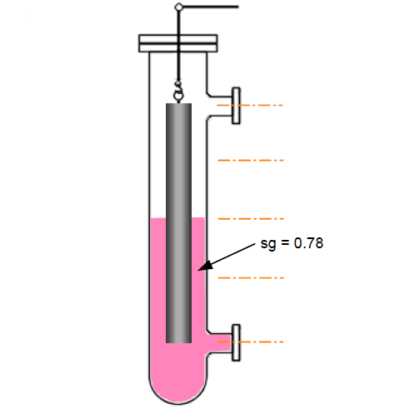
true weight of displacer = 0.25 × 490 = 122.5 lbs
volume of oil displaced = 0.25 × 0.5 = 0.125 cubic feet
weight of oil displaced = (0.125 × 0.78 × 63) lbs = 6.143 lbs
∴ Apparent weight of displacer = true weight − displaced weight
Apparent weight of displacer = 122.5 − 6.143 lbs = 116.36 lbs
Problem 2 :-
A steel displacer of volume 0.1 cubic feet is to be used as a level sensor in a vessel to store water.
Calculate the following;
1:- the maximum and minimum weights of the displacer.
2:- the maximum range of level able to be sensed, if the diameter of the displ. is 2 inch.
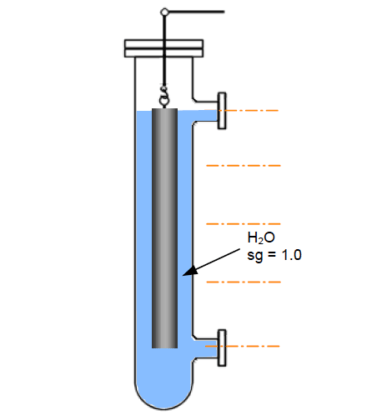
true weight of displacer = 0.1 × 490 lbs = 49 lbs
volume of water displaced = 0.1 cubic feet
weight of water displaced = 0.1 × 63 lbs = 6.3 lbs
∴ min. weight of the displacer = 49 − 6.3 lbs = 42.7 lbs
∴ max. weight of the displacer = 49 lbs
volume of the sensor = πr2L
Note : π = 3.142, 1 in = 1/12 ft = 0.0833ft
volume of the sensor ⇒ 0.1 ft3 = 3.142 × (0.0833)2 × L
0.1 ft3 = 0.0218 × L
hence, the length of displacer, L = 0.1 / 0.0218 = 4.587 ft , or 55 inches
Problem 3 :-
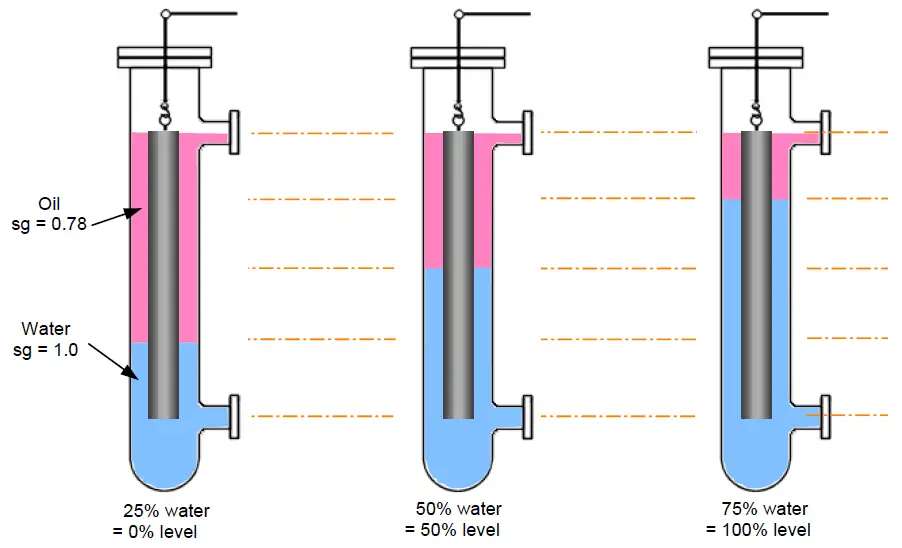
A steel displacer 1 metre long, and volume of 1000 CCs. is to be used to measure the interface level in an oil and water separator. The SG of oil is 0.78, the density of water is 1 kg/litre. Density of steel is 8000 kg per cubic meter.
Find,
1:- the diameter of the displacer.
2:- the displacer weight in air, oil & water.
3:- the “0%” and “100%” weights, if the 50% interface level is set at the displacer’s mid-point, and the span is 0.5 metres.
The displacer is assumed to be totally covered with oil or water.
volume of the sensor = πr2L
1000 c.c.s = 3.142 × r2 × 100 cm
thus, we now have, r2 = 1000 / (3.142 x 100 ) = 3.183 cm2
∴ the radius of displacer, r = Sqrt (3.183) cm = 1.78 cm
hence, the diameter of displacer = 1.78 × 2 cm = 3.56 cm
displacer’s weight in air = density × volume
Note that volume unit has to be inconsistent with density unit 1 ccs = 10−6 m3
= 8000 kgm−3 × (1×103/106) m3 = 8.0 kg
displacer’s weight in oil = (weight in air) − (weight loss in oil)
= 8.0 – (0.5 × 1 × 0.78) kg = 7.61 kg
displacer’s weight in water = (weight in air) − (weight loss in water)
= 8.0 – (0.5 × 1 × 1) kg = 7.50 kg
at 0% interface level, the displacer’s length will be covered 25% with water and 75% with oil. Hence, the displacer’s total weight will be made up of 75% of its weight in oil and 25% weight in water;
∴ displacer weight at 0% = (0.75 × 7.61) + (0.25 × 7.5) = 7.582 kg
at 50%, the displacer’s total weight will be made up of 50% weight in water, and 50% weight in oil;
∴ displacer weight at 50% = (0.5 × 7.61) + (0.5 × 7.5) = 7.555 kg
at 100%, the displacer’s total weight will be made up of 75% weight in water, and 25% weight in oil;
∴ displacer weight at 50% = (0.25 × 7.61) + (0.75 × 7.5) = 7.527 kg
Article Source : N. Asyiddin
Articles You May Like :
Conductive Level Switch Principle
Ultrasonic Level Switch Principle
Level Measurement with wet leg
DP Level Transmitter Calibration