Bernoulli’s principle is a fundamental concept in fluid dynamics that explains how the pressure within a fluid, like air or water, varies with its speed and height.
It is named after Daniel Bernoulli, who published the principle in his book Hydrodynamica in 1738.
Bernoulli’s Principle
Bernoulli’s principle can be stated as follows:
“An increase in the speed of a fluid occurs simultaneously with a decrease in the fluid’s pressure or potential energy, and vice versa.”
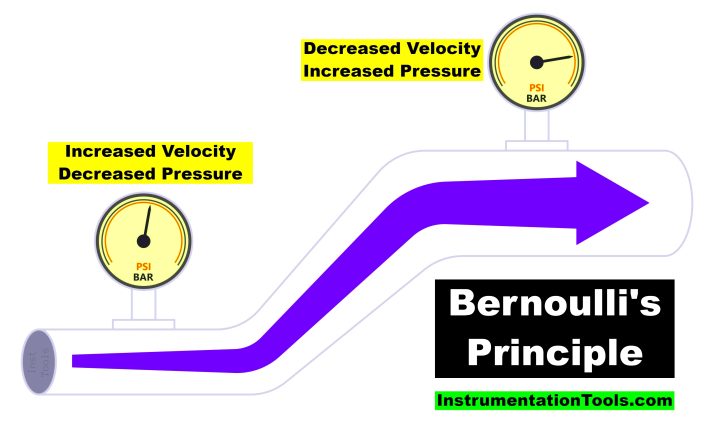
This means that if a fluid is flowing through a pipe and it reaches a section where the pipe narrows, the speed of the fluid will increase in the narrow section and the pressure will decrease. Conversely, if the fluid reaches a section where the pipe widens, the speed of the fluid will decrease and the pressure will increase.
Bernoulli’s principle is based on the law of conservation of energy. It assumes that the fluid is incompressible and that there is no energy lost due to friction (also known as a non-viscous fluid).
This principle has many practical applications, including the operation of airplane wings (the air moves faster over the top of the wing, which is curved, than underneath it, generating lift), the venturi effect (fluid pressure drops as it passes through a constriction), and even in the simple act of drinking from a straw (sucking air out of the straw increases the speed of the air in the straw and lowers the pressure, allowing atmospheric pressure to push the drink into your mouth).
Bernoulli’s Equation
Bernoulli’s Equation is a statement of the conservation of energy principle for flowing fluids, accounting for gravitational potential energy, kinetic energy, and fluid pressure. It is derived from the principles of Newton’s laws and is broadly applicable in fluid dynamics.
The Bernoulli Equation is often written like this:
P₁ + ½ρv₁² + ρgh₁ = P₂ + ½ρv₂² + ρgh₂
Where:
P₁ and P₂ are the fluid pressure at points 1 and 2.
ρ is the fluid density.
v₁ and v₂ are the fluid velocities at points 1 and 2.
h₁ and h₂ are the height of the fluid above a reference point at points 1 and 2.
g is the acceleration due to gravity.
The term P + ½ρv² is called the dynamic pressure and represents the fluid’s kinetic energy per unit volume. The term ρgh is called the fluid’s hydrostatic pressure, which represents the potential energy per unit volume.
According to Bernoulli’s equation, the sum of kinetic energy, potential energy, and pressure remains constant along a streamline assuming no work is done on or by the fluid, no heat is transferred to or from the fluid, and the fluid is incompressible and non-viscous (i.e., frictionless).
In practice, certain factors like friction (fluid viscosity), heat exchange, and work done on or by the fluid can cause energy to be added or removed from the fluid, making the equation less accurate.
However, Bernoulli’s equation provides a good approximation for many ideal fluids and many practical applications, such as aerodynamics or hydraulic systems.
Flow Measurement based on Bernoulli’s Theorem
Bernoulli’s principle is used in various types of flow measurement devices. The principle can be applied to understand and predict how a fluid’s pressure changes when its flow speed or height changes, which forms the basis for the operation of several flow measurement devices.
Here are a couple of examples:
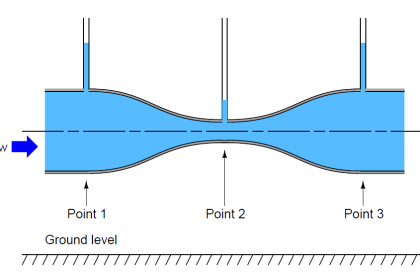
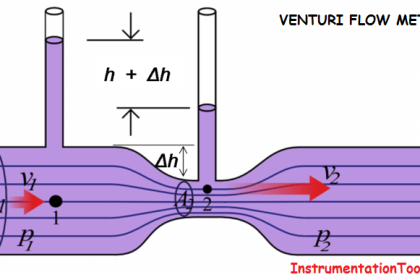
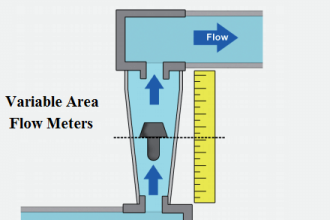
Venturi Meter
A Venturi meter is a device used to measure the flow rate of a fluid in a pipe. It consists of a pipe whose diameter gradually decreases to a throat (the narrowest point) and then gradually increases again.
According to Bernoulli’s principle, as the fluid’s speed increases in the narrow throat section, its pressure decreases. By measuring the pressure difference between the wide and narrow sections of the pipe, the flow rate can be calculated.
Pitot Tube
A Pitot tube is a pressure measurement instrument used to measure fluid flow velocity. It works by converting the kinetic energy in a fluid flow to potential energy.
When placed in a fluid flow, the fluid will come to a stop in the tube (stagnate), and by measuring the stagnation pressure and the static pressure, the fluid’s velocity can be determined using Bernoulli’s principle.
Orifice Plate
Similar to a Venturi meter, an orifice plate is placed in a pipe to constrict the flow, creating a pressure difference. This pressure difference can be used to calculate the flow rate.
In all these devices, Bernoulli’s principle is used to relate the pressure, velocity, and elevation along a streamline, providing a way to infer the velocity and therefore the flow rate of the fluid from pressure measurements.
If you liked this article, then please subscribe to our YouTube Channel for Instrumentation, Electrical, PLC, SCADA, and Industrial Automation video tutorials.
You can also follow us on Facebook and Twitter to receive daily updates.
- Orifice Sizing Guidelines
- Transmitter Calibration Frequency
- Instrumentation and Control Quiz
- Pitot Tube Troubleshooting Steps
- Ultrasonic Flow Meter Problems




nice
Very ????