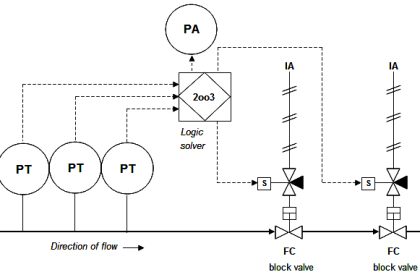
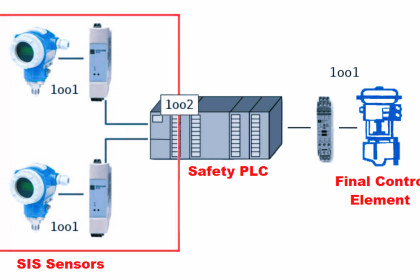
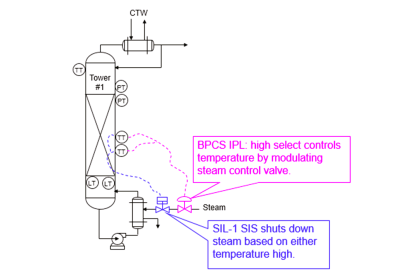
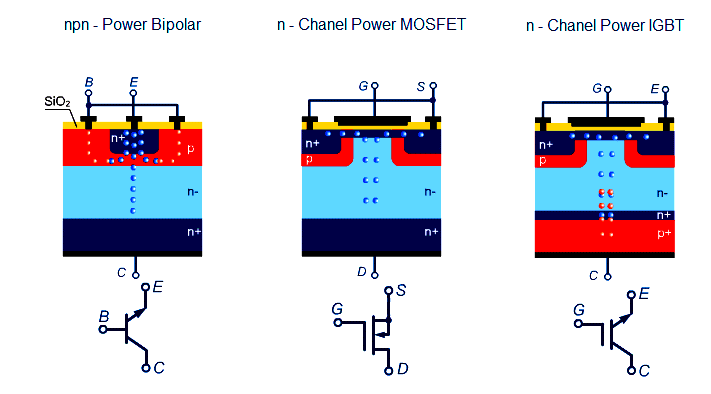
Suppose a semiconductor manufacturer creates a microprocessor “chip” containing 2500000 transistors, each of which is virtually identical to the next in terms of ruggedness and exposure to degrading factors such as heat.
The architecture of this microprocessor is such that there is enough redundancy to allow continued operation despite the failure of some of its transistors. This integrated circuit is continuously tested for a period of 1000 days (24000 hours), after which the circuit is examined to count the number of failed transistors.
This testing period is well within the useful life of the microprocessor chip, so we know none of the failures will be due to wear-out, but rather to random causes.
Supposing several tests are run on identical chips, with an average of 3.4 transistors failing per 1000-day test. Calculate the failure rate (λ) and the MTBF for these transistors.
Transistor Failure Rate Calculation
The testing scenario is one where failed components are not replaced, which means both the number of failed transistors and the number of surviving transistors changes over time like voltage and current in an RC charging circuit.
Thus, we must calculate lambda by solving for it in the exponential formula.
Using the appropriate formula, relating number of failed components to the total number of components:
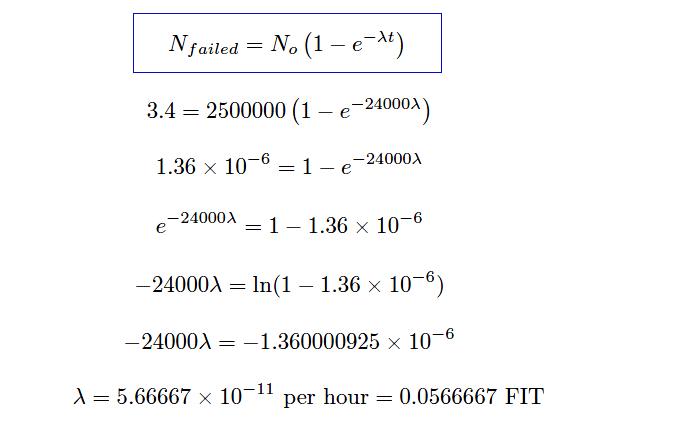
Failure rate may be expressed in units of “per hour,” “Failures In Time” (FIT, which means failures per 109 hours), or “per year” (pa).
MTBF = 1/λ = 1.7647 × 1010 hours
MTBF = 2.0145 × 106 years
Mean Time Between Failures (MTBF) is essentially the “time constant” for this decaying collection of transistors inside each microprocessor chip.