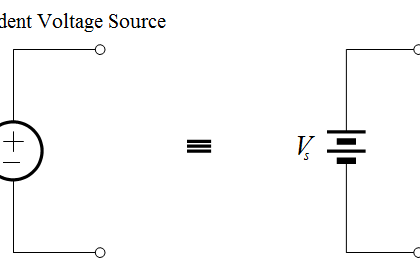
Combining Independent Sources
An inspection of the KVL equations for a series circuit shows that the order in which elements are placed in a series circuit makes no difference. An inspection of the KCL equations for a parallel circuit shows that the order in which elements are placed in a parallel circuit makes no difference. We can use these facts to simplify voltage sources in series and current sources in parallel.
Combining Independent Voltage Sources in Series
It is not possible to combine independent voltage sources in parallel, since this would violate KVL. However, consider the series connection of two ideal voltage sources shown in (a) below:
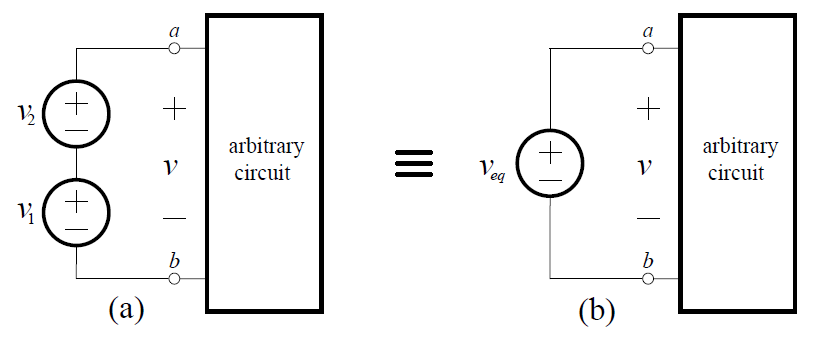
From KVL we know that v = v1 + v2 , and by the definition of an ideal voltage source, this must be the voltage between nodes a and b, regardless of what is connected to them. Thus, the series connection of two ideal voltage sources is equivalent to a single independent voltage source given by:
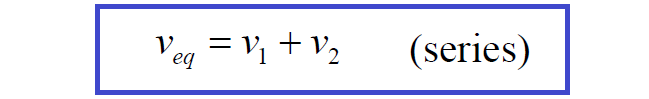
Clearly, the obvious generalization to N voltage sources in series holds.
Example
In a previous example we determined the current i in the one-loop circuit shown below:
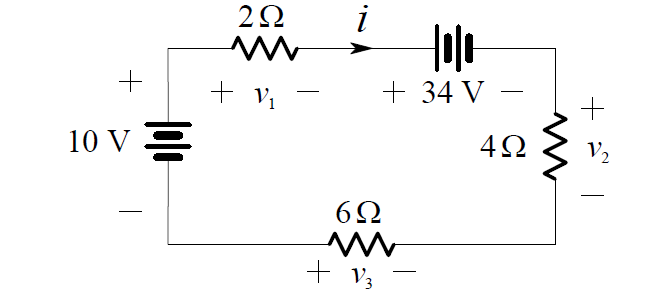
By rearranging the order in this one loop circuit (of course this does not affect i), we obtain the circuit shown below:
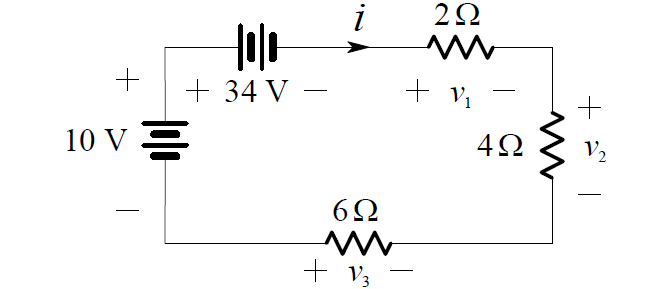
We can now combine the series independent voltage sources and the series resistors into single equivalent elements:
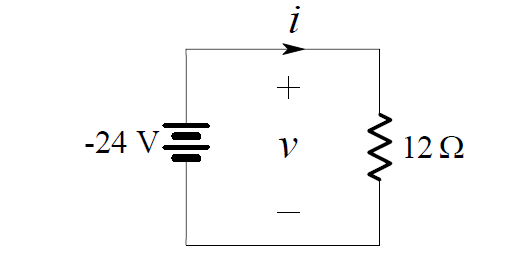
By Ohm’s Law:
i = – 24/12 = -2 A