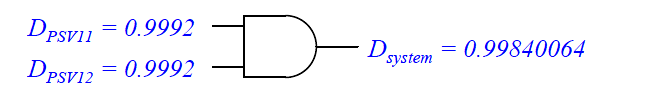The relatively simple concepts of AND and OR Boolean functions become surprisingly complicated when applying them to real-life measures of component reliability, mainly because reliability is measured in multiple ways.
As we have already seen, dependability (D) and security (S) are related concepts in that they both describe the probability of a system or system component functioning properly, but defy simple correlation because they imply different failure modes.
“Dependability” for any safety-related system or component is the probability that it will perform its safety function when called upon in an emergency. “Security” by contrast is the probability that the system or component in question will maintain normal operation when there is no emergency.
Probability Laws to a Safety Instrumented System
To illustrate, we will examine the overpressure protection features of a “knock-out drum” used to collect small amounts of liquid entrained in a gas stream.
This particular vessel is equipped with two pressure-safety valves (PSV-11 and PSV-12) designed to open and vent gas to atmosphere in the event of an overpressure condition (over 410 PSIG):
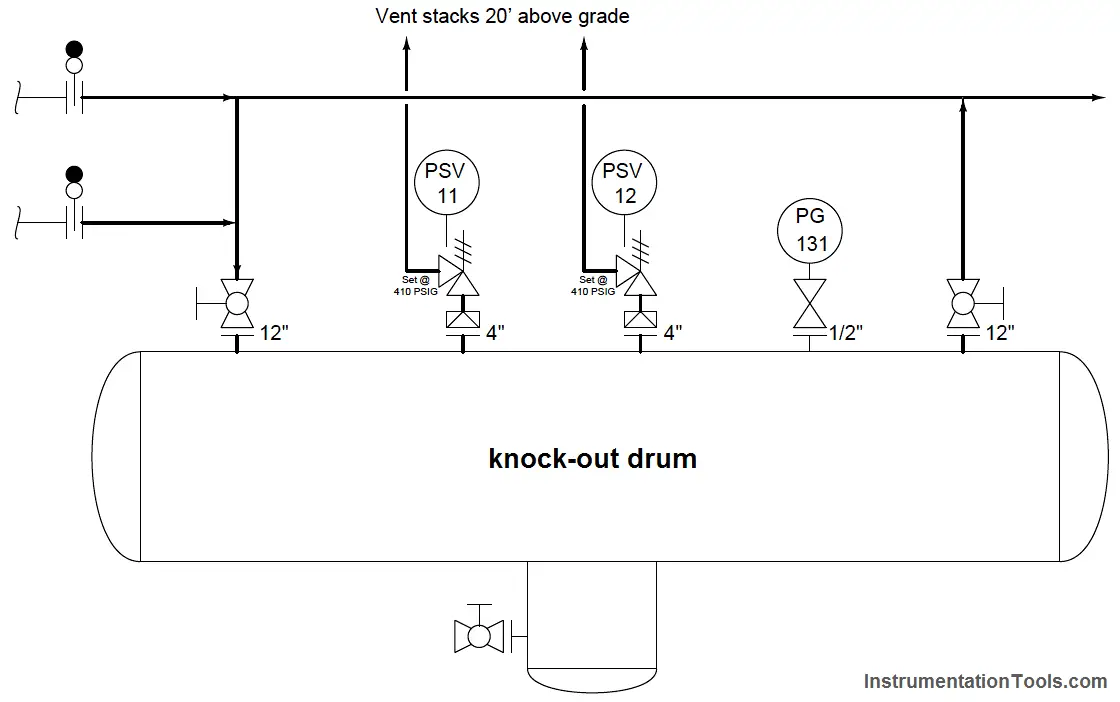
Suppose each of these pressure safety valves has a dependability (D) rating of 0.9992, which means each one has a 99.92% chance of opening up to relieve excess pressure when a high-pressure condition exists.
Let us also suppose each of these PSVs has a security (S) rating of 0.995, which means each one has a 99.5% chance of remaining in the shut condition when no overpressure condition exists.
Furthermore, assume each of the two pressure safety valves individually has a high enough flow capacity to adequately vent the vessel during an overpressure condition.
Note : An easy way to remember what each of these terms mean in the context of a protective system is to associate D (Dependability) with a dangerous scenario and S (Security) with a safe scenario: D expresses what the system or component will do when a dangerous condition presents itself to the protective system and it needs to act; S expresses what the system or component will do when conditions are safe and there is no need to act.
How might we calculate the overall dependability and security ratings of this dual-PSV overpressure protection system?
Clearly, we must use Boolean functions to combine the two valves’ D ratings into a Dsystem rating, and likewise with the two valves’ S ratings, but which logical function should we use to calculate each measure of reliability?
The choice between AND and OR functions may not be obvious at first inspection.
One way to analyze logical functions is in terms of what state (0 or 1) at any input will guarantee a certain output state. For an AND function, any 0 state in guarantees a 0 state out. For an OR function, any 1 state in guarantees a 1 state out.
These facts are useful when selecting logical functions for a variety of purposes, and they will serve us well in this application of probability values too.
A useful problem-solving technique for this application is called limiting cases, where we take some quantity to its extreme limits in an effort to simply the problem at hand.
To begin, we will assume that one of the two pressure safety valves in this system has a D rating of 1, which means it is perfectly reliable when called to open by a high-pressure condition. A D rating of 1 is a “limiting case” of the pressure safety valve’s dependability: a perfectly dependable PSV.
If this were true, would it guarantee the whole overpressure protection system is dependable, or not? Since we know each valve is sized large enough to protect the vessel on its own (without need of the second PSV opening), then the answer to this question is “yes”: a single PSV with a D rating of 1 guarantees a Dsystem rating of 1.
All we need is for one of these PSVs to vent when it senses a high-pressure condition to protect the vessel from overpressure damage. Therefore, the proper Boolean function to calculate Dsystem from the valves’ individual D ratings is the OR function, because given the choices of AND and OR only the OR function guarantees a certain output state with any “1” input. Calculating system dependability using both valves’ D ratings:

The numerical results shown here should make sense: in an overpressure protection system where we only need one of the two valves to vent gas during an overpressure condition, having two valves increases the probability that the vessel will be adequately protected.
Now we will apply this same problem-solving strategy to the system’s security (S). Taking the high limiting-case value of either PSV’s S rating, we ask ourselves the question “Does any one perfectly secure PSV (S = 1) make the system secure?”
In other words, if one of these valves was guaranteed not to vent when no overpressure condition exists, would that mean the entire system was guaranteed not to vent when it didn’t need to? The answer here is “no”, since the presence of two pressure safety valves increases the chance of unnecessary leakage.
This tells us we cannot use the OR function for security, because a perfectly secure PSV (S = 1) does not guarantee a perfectly secure system.
At this point we may conclude that the proper Boolean function for system security in this application is the AND, by process of elimination. However, we may also consider a different limiting case scenario to verify this conclusion.
Let us suppose one of the pressure safety valves failed in such a way that it had zero security, meaning there was no chance at all it would remain shut when no overpressure condition existed (i.e. a security rating of S = 0 means it is guaranteed to vent when it shouldn’t).
Would one PSV in this state guarantee a certain system security state? We see here that this is true: any one PSV with an S rating of zero means the system as a whole has a zero S rating as well, because all it takes is one PSV to unnecessarily vent to make the system as a whole unnecessarily vent.
Since we know the Boolean AND function guarantees a zero output for any zero input, this is the function we should use when calculating system security. Calculating system security using both valves’ S ratings:

These numerical results should make sense as well: in an over-pressure protection system where a leak in one valve is enough to constitute a problem, the presence of multiple valves is a liability and therefore reduces the over-all security.
It is worth noting that a simple change in parameters may strongly impact our reliability calculations. In this scenario we were told each pressure safety valve was sized large enough to adequately vent the vessel on its own, without the help of the other PSV, in the event of an over-pressure condition.
What if the PSVs were undersized, and both of them would be required to vent in order to protect the vessel from over-pressure damage? How would this alteration impact our reliability calculations?
It should be obvious that this change will have no effect whatsoever on the system’s security, because it still takes just one PSV to leak in order to make the whole system unsecure.
However, dependability will definitely be affected by this change because now a single PSV with a D = 1 rating is not enough to guarantee a protected system. With undersized PSVs, both valves must be dependable in order to guarantee dependable over-pressure protection.
Conversely, if only one of the PSVs fails in such a way as to be completely undependable (D = 0, meaning the valve is guaranteed to fail in the shut condition when faced with high pressure), it makes the whole system undependable because the other valve on its own is not enough to adequately vent the excess gas.
From this analysis we can see that the proper Boolean function for dependability will now be AND, because any zero into an AND function guarantees a 0 output. Re-calculating dependability for undersized PSVs: