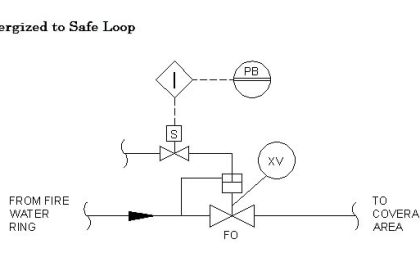
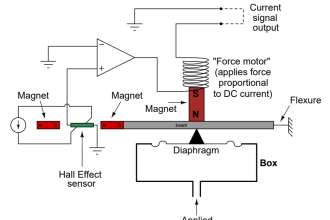
The closed-loop, or “Ultimate” tuning method of Ziegler and Nichols was applied to this process.
Eliminating both integral and derivative control actions from the controller, and experimenting with different gain (proportional) values until self-sustaining oscillations of consistent amplitude (Note) were obtained, gave a gain value of 11, as shown in below figure.
Note : The astute observer will note the presence of some limiting (saturation) in the output waveform, as it attempts to go below zero percent.
Normally, this is unacceptable while determining the ultimate gain of a process, but here it was impossible to make the process oscillate at consistent amplitude without saturating on the output signal.
The gain of this process falls off quite a bit at the ultimate frequency, such that a high controller gain is necessary to sustain oscillations, causing the output waveform to have a large amplitude.
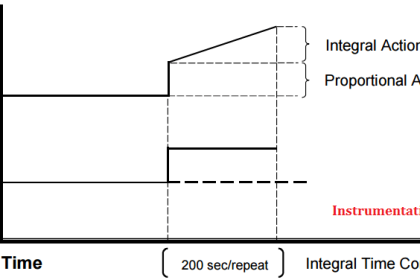
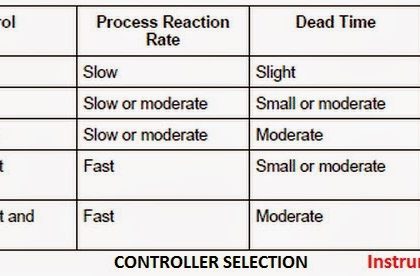
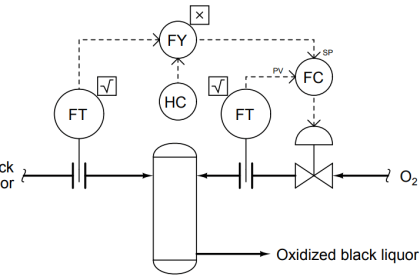
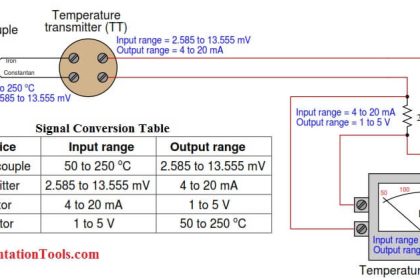
Ziegler-Nichols Closed Loop Tuning
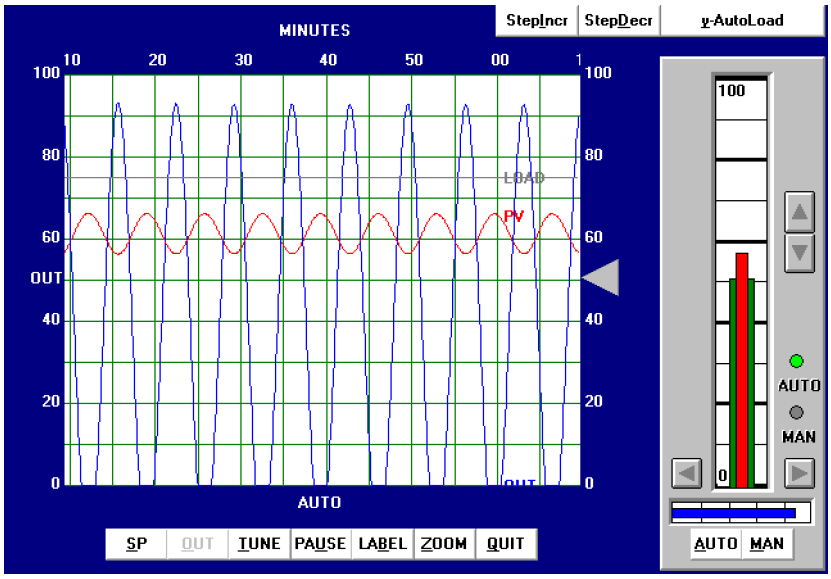
From the trend, we can see that the ultimate period (Pu) is approximately 7 minutes in length. Following the Ziegler-Nichols recommendations for PID tuning based on these process characteristics:
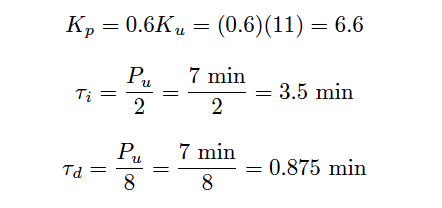
It should be immediately apparent that these tuning parameters will yield poor control. While the integral and derivative values are close to those predicted by the open-loop (Reaction Rate) method, the gain value calculated here is even larger than what was calculated before.
Since we know proportional action was excessive in the last tuning attempt, and this one recommends an even higher gain value, we can expect our next trial to oscillate even worse.
Applying the PID values of 6.6 (gain), 3.5 minutes per repeat (integral), and 0.875 minute (derivative) gave the following result in automatic mode:
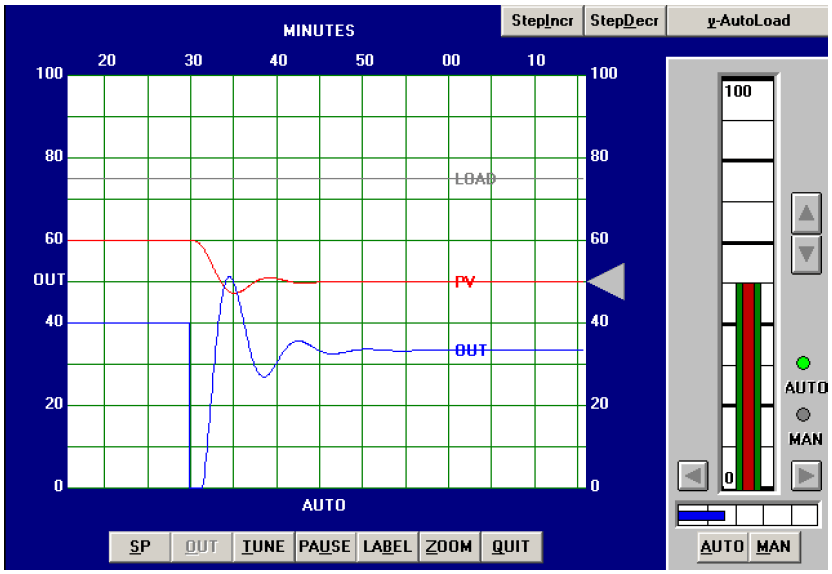
This time the loop stability is a bit worse than with the PID values given by the Ziegler-Nichols open-loop tuning equations, owing mostly to the increased controller gain value of 6.6 (versus 4.5).
Proportional action is still the dominant mode of control here, as revealed by the minimal phase shift between PV and OUT waveforms (ignoring the 180 degrees of shift inherent to the controller’s reverse action).
In all fairness to the Ziegler-Nichols technique, the excessive controller gain value probably resulted more from the saturated output waveform than anything else. This led to more controller gain being necessary to sustain oscillations, leading to an inflated Kp value.