When calculating the power dissipation of resistive components, use any one of the three power equations to derive the answer from values of voltage, current, and/or resistance pertaining to each component:
Power Calculations
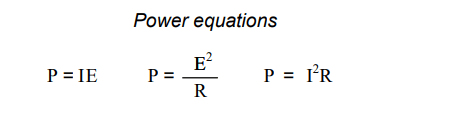
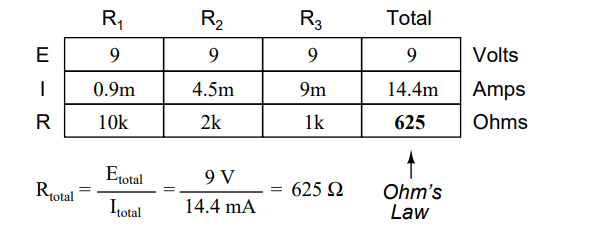
This is easily managed by adding another row to our familiar table of voltages, currents, and resistances:
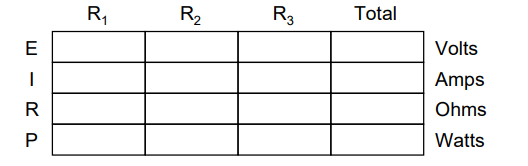
Power for any particular table column can be found by the appropriate Ohm’s Law equation (appropriate based on what figures are present for E, I, and R in that column).
An interesting rule for total power versus individual power is that it is additive for any configuration of circuit: series, parallel, series/parallel, or otherwise.
Power is a measure of rate of work, and since power dissipated must equal the total power applied by the source(s) (as per the Law of Conservation of Energy in physics), circuit configuration has no effect on the mathematics.
Review:
- Power is additive in any configuration of resistive circuit: PTotal = P1 + P2 + . . . Pn