Power supply circuits are a class of circuits that are designed to convert electrical energy for some load.
Power Supply Circuits
Every power supply consists of at least three parts:
- An input power source, which delivers power at some voltage or range of voltages V1
- A load, which requires power delivered at some voltage or range of voltages V2
- Conversion circuitry, which receives voltage V1 as an input and generates voltage V2 as an output
Some devices are simple enough that they can operate properly without any modifications to the voltage and current provided by the input source.
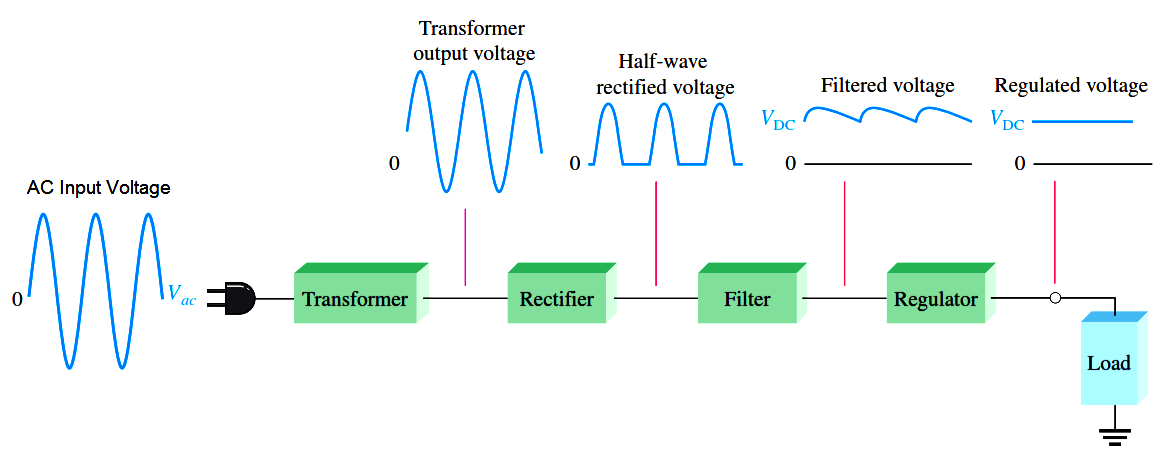
For example, the lightbulb inside a low-cost flashlight is designed to emit light when connected in series with a few batteries, meaning the entire conversion circuit is just wires.
In a similar way, household incandescent lightbulbs are designed to operate properly when connected to an AC source, operated at a well-regulated voltage and line frequency.
But for the majority of electronic devices, it is impractical to operate an entire circuit at voltages commonly available. Computers, cell phones, car stereos, aircraft sensors, traffic lights, and pacemakers all have elements which require drastically different voltages than those delivered by any common power source.
Well-designed power supply circuits convert almost all of the energy supplied by batteries, solar cells, AC lines and other power sources to voltage levels suitable for the operation of intricate electronic devices.
These are some of the typical considerations when designing a power supply circuit:
Efficiency
Efficiency is defined as the output power divided by the total input power. The maximum theoretical efficiency of a circuit is 100%, and this makes sense: the only place output power can come from in a power supply is the input power source.
Energy that is consumed in the conversion process, and is not delivered as output power, is called power loss. All power supply circuits have some losses, even if those losses are very small. Maximizing efficiency and minimizing losses is of key importance in power supply design.
Highly efficient devices can last longer on a single battery charge, cost less money to operate from a utility AC line, and generate less heat.
Heat
Power loss is dissipated away from a power supply circuit as heat. Very small semiconductor components may only be able to dissipate a few hundred milliwatts before they become too hot and fail. On the other hand, very large power supplies can convert multiple kilowatts of power, and routinely see tens of watts dissipated across only a few components.
Further complicating issues, many power supplies are designed to operate in hot or cold environments, where temperatures can vary by over 100o C. At hotter temperatures, devices must be thermally derated to avoid overheating, which significantly reduces the maximum output power available.
At colder temperatures, considerable deviations in component values can be expected, and rapid changes in loading can lead to thermal shock effects, where repeated heating and cooling stresses components to failure.
In most cases, cold temperature performance can be guaranteed with proper component selection; removing waste heat and preventing damage from overheating receive much greater consideration.
In order to prevent component failures, high dissipation components are usually connected to heat sinks. Sometimes the only heat sink needed is a solid connection to a copper plane in a printed circuit board. But for anything beyond a few watts, components need to be connected to a separate, thermally conductive metal block.
By putting long metal fins on these blocks, the surface area can be boosted to increase convective heat transfer. A fan can also be used to increase airflow. Some designs even use water or oil traveling through the block to more effectively remove waste heat.
As a general rule, most semiconductors begin experiencing damage when the circuit\’s internal temperature reaches 150oC, though some devices are designed to withstand even higher temperatures.
Other components such as inductors and capacitors are available in a wide range of operating temperatures and tolerances, with a premium charged for more extreme temperatures and tighter tolerances.
Size
In some devices such as cell phones or smart watches, there can be dozens or hundreds of components made to fit within only a few square centimeters. Power supply circuits in these types of devices must be small leave room for other, feature-rich components.
In other devices such as aircraft electronics, the power requirements are large enough that many components must be attached to a heat sink. This can add significant weight to the overall design, which reduces fuel economy of the aircraft.
Size is directly related to the amount of power being converted, and the efficiency of the conversion. The more power being converted, the larger the components must be to spread out self-heating and to withstand the high voltages used for larger power conversions. Improvements in efficiency can help to reduce supply size, since less heat sinking is required.
Cost
Unsurprisingly, cost is a critical factor. Generally, as both power and efficiency are increased, the cost of the power supply increases as well. This cost increase comes from a combination of expensive but well-optimized components, increased complexity leading to longer design and test cycles, and costs associated with regulatory compliance.
As in any engineering challenge, power supply design is a tradeoff of acceptable performance and cost. Since all electronic devices require one or more power supply circuits, aggressive cost optimization is common. In high-volume manufacturing, saving even a few cents per product can reduce build costs by thousands of dollars.
Line Regulation
Line regulation is a measure of how well a power supply circuit can respond to changes in input source voltage. Many input power sources present a wide voltage range to a power supply input: battery voltages can vary by 30% or more across one charge cycle, solar cell voltages vary proportionally to incident sunlight, and AC line voltages can (on rare occasion) deviate by as much as 20% in either direction.
Line regulation is defined as the output voltage at the maximum/minimum input voltage, minus the output voltage at the nominal input voltage. It can also be given as a percentage of the nominal output voltage value. An ideal power supply has perfect line regulation, ±0V or ±0% change. It is not uncommon for modern power supplies to see values < ±5mV or < ±0.1%.
Load Regulation
Load regulation is a measure of how well a power supply circuit can respond to changes in output loading. As output power increases, heating from power loss causes changes in reference parameters used by the circuit to control the output.
Power supply designers use carefully designed reference circuits to minimize the effects of temperature variations, but observable effects still exist. Load regulation is defined as the output voltage at full load, minus the output voltage at no load.
It can also be given as a percentage of the nominal output voltage value. An ideal power supply has perfect load regulation, 0V or 0% change. Modern power supply circuits can achieve values similar to line regulation.
Ripple Rejection
For many power supply circuits with an AC line as input, the line frequency is coupled through the supply to the output.
Some power supply circuits specify a ripple rejection, usually in dB, which is defined as the magnitude of a specific frequency on the output (commonly 100Hz or 120Hz) relative to the magnitude of that same specific frequency on the input.
Quiescent Current
Even at no load, some power is required to keep a power supply in regulation. The housekeeping current used to power the control circuitry of the supply is called the quiescent current. This value has a wide range, spanning from hundreds of milliamps all the way down to hundreds of nanoamps.
Output Impedance
An ideal voltage source has zero output impedance. Practical converters see some small output impedance, which tends to grow at higher frequencies.
For a power supply to effectively regulate against loads that change in milliseconds or less, low output impedance is mandatory. Otherwise, sudden changes in load current will produce severe changes in output voltage.
Nearly all converters can easily achieve output impedances of less than an ohm; < 10mΩ at DC is not uncommon.
Output Voltage Noise
Electrons flowing in resistors and transistors are susceptible to thermodynamic events, statistical fluctuations in current density, and other complex particle-scale phenomena. These tendencies manifest in all circuits, including power supply circuits, as noise on the output voltage.
Although the average value of a power supply output is constant, noise can cause the output to experience millivolt excursions on a microsecond or submicrosecond scale.
For lower power analog circuits that depend on tightly regulated power supply voltages such as high-resolution analog-to-digital converters or high-frequency oscillators, power supply noise can cripple performance.
Because noise sources tend to be a function of frequency, noise is commonly listed as a value integrated over a frequency range (in RMS Volts), or is specified as a plot of noise spectral density comparing noise (in Volts/Hz) vs. frequency.
Wideband (10Hz to 100kHz) integrated noise can be controlled to < 10µVrms, and noise at high frequencies can approach < 10nV/Hz.
Higher power designs tend to introduce noise on the order of tens or hundreds of millivolts, concentrated at specific frequencies, as a function of their construction. Though some designs exist which can tightly control even high-power supply noise, they are costly and are therefore reserved for specialized test and measurement equipment.
Virtually all practical power supplies above a few watts will generate millivolts of noise on the output, and for many types of load this does not affect device performance in the slightest. It is common to use an effective but noisy power supply for insensitive loads, and as the input to a second, quieter power supply.
Linear Power Supplies
There are two major types of power supplies whose output behavior can be determined according to linear equations: shunt regulators, and series regulators. Shunt regulators (pictured in Figure below are so named because they shunt away unnecessary load current to keep the output in regulation.
In a shunt regulator, high quiescent current is necessary, since the shunt must be able to redirect the full load current at no load conditions. This can lead to high power dissipation, especially for appreciably large full load currents.
On the bright side, they are relatively simple, often made of entirely passive elements, and can be reduced to two-terminal devices.
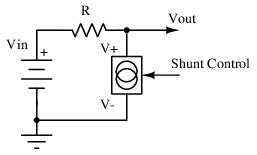
Shunt regulators
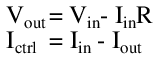
Series regulators, in contrast, regulate the input current with a pass element to control the output current delivered to a load pictured in Figure below. This can be utilized to reduce quiescent current to almost nothing at light or no load, though some current must always pass through the series element to ensure proper output voltage regulation.
However, the series regulator must control both the voltage drop across and the current through the series element to regulate the output voltage, and no passive element can be used to guarantee this behavior. Because of the need for some form of output sensing circuitry, a three terminal solution is almost always required.
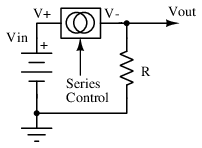
Series regulators
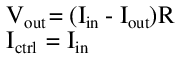
For the sake of illustrating the common terms seen in power supply design, consider the following specification: Suppose there is a need to take a static 15V output from a converter, and step it down to a 5V level.
The input voltage may vary by as much as ±3V, and the output current must be 500mA maximum. In the following examples, several basic topologies will be explored, and the relative strengths and weaknesses of the different approaches compared.
Resistor divider power supply
Example Supply: Resistor Divider
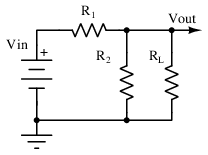
Resistor divider power supply
The humble resistor divider circuit of Figure above is perhaps the simplest power supply circuit. While its behavior is entirely linear, it is hard to say whether such a supply should be considered a shunt or series regulator, since the output voltage is a function of both the shunt and series elements.
For the purposes of this first example, the distinction is unimportant. The nonidealities of this circuit, especially when constrained by the specification above, make it useful to conceptualize the common terms used in power supply design.
The resistor values must be small to simultaneously allow 500mA through the pass element without causing too much of a voltage drop, and maintain a nominal output voltage of 5V from a 15V supply. The values 15Ω and 7.5Ω are selected for R1 and R2, respectively.
The behavior of the circuit can be described by a system of equations, first using ohm\’s law at the output, second by using the standard divider equation considering R2 and the load in parallel:
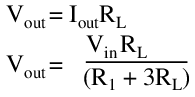
By selecting values for Vin and one other parameter, and solving for the remaining unknowns, the performance of this circuit may be interrogated. The key points are summarized below.
Efficiency
To achieve the maximum output current of 500mA with nominal input conditions (Vin = 15V), solving the system of equations gives:
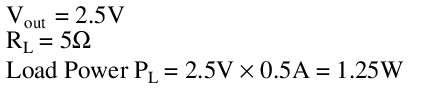
Meanwhile, the input power is the input voltage multiplied by the input current, and the input current is found as:
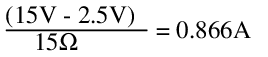
Therefore,
![]()
Our efficiency at full load is then:
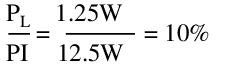
It can also be shown using calculus that the maximum efficiency is achieved with a load resistance of 5Ω, yielding only 10.1% efficiency. These values are unimpressive.
Interestingly, a quick calculation will reveal that this maximum efficiency is the same, regardless of input voltage. This makes sense, since output power is ratiometric with input power for the same circuit.
Quiescent Current
At no load, the circuit draws:
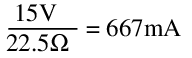
This is more than the maximum output by some margin, and is very wasteful compared to what might be achievable with other topologies. Worse still, the total current only increases with increasing load.
Heat
At no load, the circuit dissipates 10W power, and at full load this increases to 12.5W. Under short circuit conditions, this increases to 15W, all dissipated in R1.
Both R1 and R2 would need to be large wirewound resistors, or would require active cooling, for this supply to function at ambient temperature. Performance above ambient temperature is more difficult.
Load regulation
At full load, the output voltage drops from 5V to 2.5V. From the load regulation equation, we find that this supply has the following load regulation:
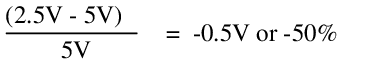
This is atrocious. Any improvement in load regulation is also practically infeasible; to make the parallel combination of R2 and the load negligibly different from the load, even at full load, the value of R1 and R2 would need to be further decreased by more than an order of magnitude, which would necessarily increase the quiescent current and decrease the efficiency by the same degree.
It is unreasonable to require over 100W of power dissipation to maintain a reasonable load regulation from a resistor divider. Ideally, it shouldn\’t even take milliwatts.
Line regulation
At 18V with no load, the output voltage is:
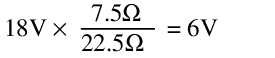
Meanwhile, at 12V, the output voltage is:
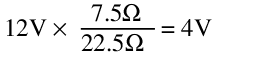
This corresponds to a line regulation of ±1V, or ±20%. This is quite terrible.
While on the subject of input voltage variations, consider that the values of quiescent current and load regulation will change for different input voltages. As the input voltage increases, the quiescent current increases, and the heat generation increases.
The output will deliver 500mA to a 7Ω load at 3.5V. At <15V the output voltage decreases substantially, delivering 500mA to a 3Ω load at 1.5V. Since the output voltage is directly proportional to the input voltage, the output is dependent on a stable input voltage, which is not always possible.
Output Impedance
By small signal analysis, the voltage source at Vin is shorted, and the output impedance is plainly the parallel combination of R1||R2, or 5Ω.
Since this output impedance is static across all changes in input voltage and output current, it is understandable why the output voltage varies so much with every change in input and load conditions.
Output Noise
Although this resistor will be affected by thermal noise, standard 1/f noise, and excess noise due to resistor construction, ultimately noise is unlikely to be the biggest concern in this design, and true noise analysis will be saved for more deserving circuits.
The performance of this circuit as a power supply is nothing short of abysmal. In fairness to the resistor divider, the most common use for such a circuit is voltage division into high-impedance loads, such as amplifier input pins and transistor gates.
For these high-impedance load conditions, the divider may be treated as very close to ideal, and as such it is not often thought of as a power supply circuit.
Nevertheless, when operating conditions begin to change (such as with supply voltage variations or even small load current increases), high impedance amplifier inputs and transistors can still be made to misbehave.
In this impractical example it should be clear that a resistor divider is unsuited for any serious power delivery, with completely unusable line and load regulation and horrible overall efficiency. However, with only a minor modification, this circuit can be augmented with vastly improved line and load regulation. This is explored in the following example.
Zener Divder Power Supply
Example Supply: Zener Divider
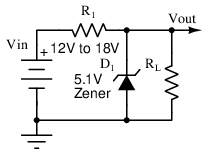
Zener Divder Power Supply
The circuit of Figure above is a Zener divider (Zener diodes are discussed in chapter 3). By substituting a reverse-biased Zener diode in place of R2 in the previous circuit, the shifting Zener impedance above a certain reverse current knee point can be exploited to guarantee a stable output voltage over different line and load conditions.
Keeping in mind that Zener diodes can only be constructed with certain reverse voltages, the closest stable output to 5V is chosen, giving a Zener voltage of 5.1V. At no load, all available current will be passed through the Zener diode.
By choosing this load current to be slightly over 500mA at maximum load (say by 10mA), regulation can be ensured even when the the full load current is delivered to the load. R1 is selected for all voltages within the tolerance of the input voltage range: the worst case, at 12V, requires that:
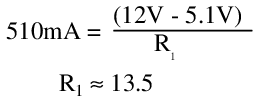
As long as the Zener diode has current through it, a load of 10.2Ω can now be attached, with any input supply voltage in the specified range, and 500mA will be delivered to it.
To prove this assertion, test the behavior at Vin = 12V and Vin = 18V:
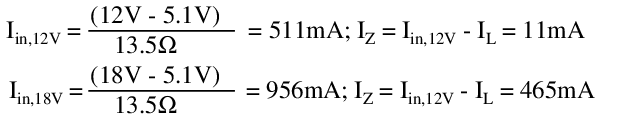
In theory, this design should therefore be capable of meeting all the requirements. A closer examination of the affected parameters offers some caveats.
Efficiency
The Zener regulator efficiency differs depending on input voltage and output loading. The best case efficiency for any input voltage is at full load, and the best case efficiency for any load is at the minimum input voltage.
In this condition, we find that:
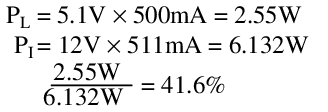
This is better than the resistor divider, but not by much, and only at one extreme corner of operation. At the other corner the results are less impressive:
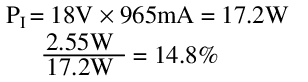
Quiescent current
At no load, the full operating current of the Zener regulator must travel through the Zener diode. Best case, this is always more than the maximum output current; worst case, it can be much greater.
At 17V, this regulator consumes almost double the maximum output current!
Heat
Since the Zener regulator quiescent current is always greater than the maximum operating current, the worst case power dissipation leads to a great deal of heat dissipated in both R1 and in the diode.
However, as the load current increases, the Zener diode dissipates less and less power, since the current and therefore the power must be diverted from the diode to the output load.
Meanwhile, R1 power dissipation remains almost constant across loading, but benefits from a lower input voltage. If for any reason the output current exceeds the quiescent current (such as during a short circuit), the power dissipation in R1 increases above the typical worst case operating point, requiring a larger component or better cooling to endure this stress.
Even under normal operating conditions, R1 still dissipates enough to require a large wirewound resistor and probably some form of active cooling:
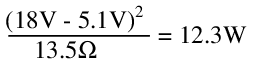
It is worth noting, in passing, that at worst case the Zener diode must dissipate close to 5W; while there exist Zener diodes capable of this, 5W is an uncommonly large value for a Zener diode. With smaller maximum load current requirements, low power Zeners may be used at substantially decreased costs.
Line and load regulation
From an ideal standpoint, the Zener voltage is always 5.1V, across all line and load conditions. In reality, however, the Zener diode has some temperature related effects which cause the Zener voltage to change. Worse still, the temperature effects do not all act in the same direction.
Low voltage Zener diodes behave predominantly according to the Zener effect, an electron tunneling process, which has a negative temperature coefficient (Zener voltage decreases with increasing heat).
Higher voltage Zener diodes behave predominantly according to the avalanche effect, a form of current multiplication that has a positive temperature coefficient (Zener voltage increases with increasing heat).
At around 4V to 6V, and dependent on the Zener current, the temperature coefficients of these two mechanisms will combine and can occasionally cancel out almost entirely.
Unfortunately, there is still some effect at 5.1V; A 5W rated 1N5338B, for example, can see a difference of almost 0.4V across temperature, typically increasing in voltage.
A basic approximation of this effect can explain the difficulty. With a 15V supply voltage, at no load the Zener current and power are found to be:
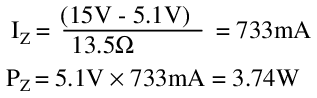
Assuming the change in Zener voltage is up to 0.4V at 5W for the given Zener diode, and the change is both linear and positive, the Zener voltage may increase in response to increasing junction temperature by as much as:
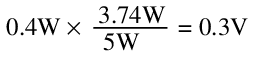
This changes the Zener current and power to:
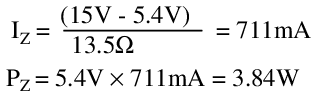
Iteration shows this change in Zener voltage with temperature eventually stabilizes; still, the output is far from its ideal value. As load current increases, Zener current decreases, returning the output voltage to a lower value.
Line and load regulation are difficult to estimate precisely, since the exact location of the Zener knee, the effect of process variation on the temperature coefficient, and the variation of the temperature coefficient with Zener current cannot always be predicted.
Both are frequently verified experimentally or with a spice simulation. Broadly speaking, with a maximum specified regulation swing of about 0.4V, and assuming this can be either positive or negative for a 5.1V Zener diode, the combined line and load regulation can be stated as:
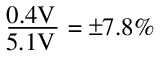
Output Impedance
For the small signal analysis, voltage sources are shorted. The impedance looking into the output is just R1||RZ.
But RZ is a dynamic value, based on the Zener voltage (Vout) and the Zener current (Iz).
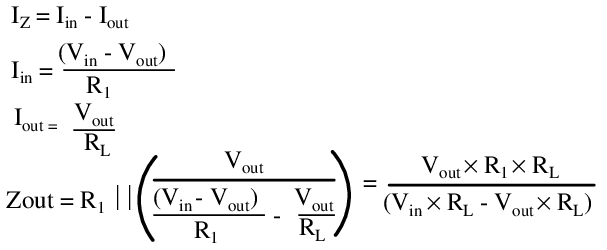
In the limit as RL approaches infinity, Zout becomes Vout x R1 / Vin, approximately 4.59Ω at 15V input. Interestingly, from this equation we can discover that the output impedance increases as a function of increasing load, to a maximum of R1 at a dead short across the output. The output is regulated because the output impedance continuously changes to match the level of loading.
Output Noise
The topic of output noise for Zener diodes is complicated. Due to the different mechanisms of Zener diode behavior, there are different sources of noise for different Zener voltages and currents. Some attempt to simplify these topics will be made here.
Low voltage Zener diodes operate on the Zener effect, where discrete electrons tunnel across a barrier. Since this is a discrete, random process centered around a mean value, it follows a Poisson distribution and generates corresponding shot noise.
The noise level is proportional to the square root of the number of discrete events. Thus, as current increases, shot noise increases as well. For a given Zener current IZ and Zener voltage VZ and recalling the electron elementary charge q = 1.6 x 10-19 coulombs, the shot noise is:
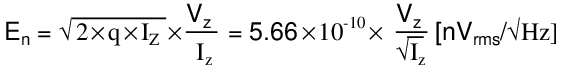
At no load, this effect is almost negligible, since it is inversely proportional to IZ. But at full load, IZ shrinks considerably. The noise at full load for Vin = 12V is 7x worse than the noise at no load. At 18V, since the difference in IZ at no load and at full load is smaller, the effect is much less pronounced.
High voltage Zener diodes operate on the avalanche effect, where one carrier collides with many others and causes an avalanche multiplication of carrier movements, resulting in wide-bandwidth noise that can exceed simple shot noise by orders of magnitude.
In fact, the equation is almost identical, but depends to some extent on the recombination lifetime of each new electron in the avalanche. Without getting too deeply into the physics, it is usually sufficient to introduce some large multiplier to the original shot noise equation.
Whereas a low voltage Zener diode might measure its wideband noise in the hundreds of nV, a high voltage Zener diode might measure its wideband noise in hundreds of µvolts or even low millivolts.
To keep a Zener diode at the lowest possible noise, there are only two requirements: first, use a low voltage Zener diode, to minimize avalanche noise; second, use a large Zener current, even at full load.
Though increasing the current increases the power dissipation, potentially leading to greater thermal noise, remember that thermal noise is proportional to Zener impedance, and that Zener impedance shrinks faster than absolute temperature grows.
In power supply design Zener noise is once again rarely an issue, since other regulators can be created with less noise, more efficiency, and better line and load regulation.
In general, shunt regulators are used in cases where the power dissipation is negligible, and the load current is small (tens of milliamps or fewer). More complex shunt regulators can incorporate compensation schemes which minimize the effects of line, load, and temperature variations.
The exact mechanisms of these compensation schemes are beyond the scope of this discussion, but line and load regulation values of <1% are achievable with shunt regulation schemes, over a very wide range of temperatures and input voltages.
