Let’s begin with a semiconductor gate circuit in need of simplification. The “A,” “B,” and “C” input signals are assumed to be provided from switches, sensors, or perhaps other gate circuits. Where these signals originate is of no concern in the task of gate reduction.
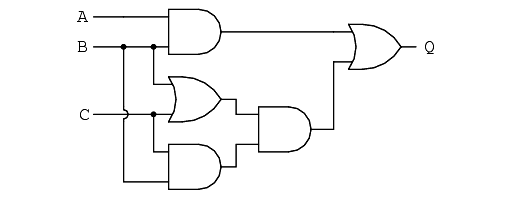
Our first step in simplification must be to write a Boolean expression for this circuit. This task is easily performed step by step if we start by writing sub-expressions at the output of each gate, corresponding to the respective input signals for each gate.
Remember that OR gates are equivalent to Boolean addition, while AND gates are equivalent to Boolean multiplication.
For example, I’ll write sub-expressions at the outputs of the first three gates:
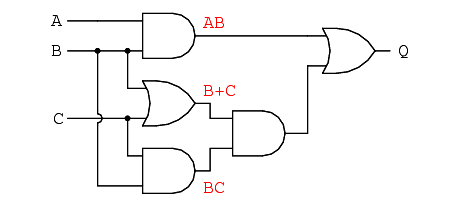 . . . then another sub-expression for the next gate:
. . . then another sub-expression for the next gate:
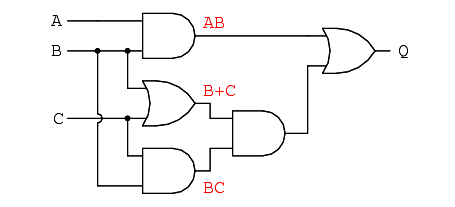
Finally, the output (“Q”) is seen to be equal to the expression AB + BC(B + C):
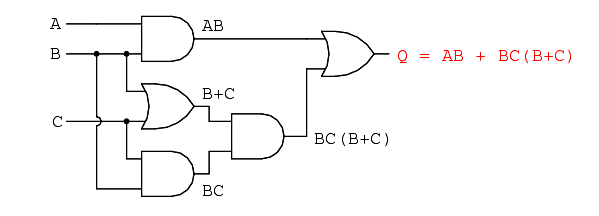 Now that we have a Boolean expression to work with, we need to apply the rules of Boolean algebra to reduce the expression to its simplest form (simplest defined as requiring the fewest gates to implement):
Now that we have a Boolean expression to work with, we need to apply the rules of Boolean algebra to reduce the expression to its simplest form (simplest defined as requiring the fewest gates to implement):
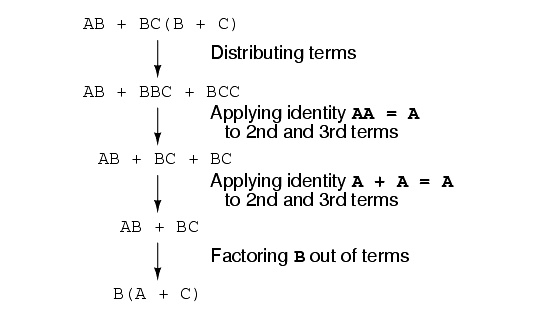
The final expression, B(A + C), is much simpler than the original, yet performs the same function. If you would like to verify this, you may generate a truth table for both expressions and determine Q’s status (the circuits’ output) for all eight logic-state combinations of A, B, and C, for both circuits. The two truth tables should be identical.
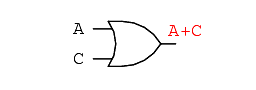
Now, we must generate a schematic diagram from this Boolean expression. To do this, evaluate the expression, following proper mathematical order of operations (multiplication before addition, operations inside parentheses before anything else), and draw gates for each step.
Remember again that OR gates are equivalent to Boolean addition, while AND gates are equivalent to Boolean multiplication. In this case, we would begin with the sub-expression “A + C”, which is an OR gate:
The next step in evaluating the expression “B(A + C)” is to multiply (AND gate) the signal B by the output of the previous gate (A + C):
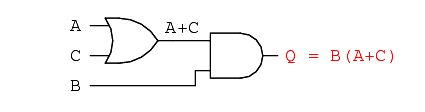 Obviously, this circuit is much simpler than the original, having only two logic gates instead of five. Such component reduction results in higher operating speed (less delay time from input signal transition to output signal transition), less power consumption, less cost, and greater reliability.
Obviously, this circuit is much simpler than the original, having only two logic gates instead of five. Such component reduction results in higher operating speed (less delay time from input signal transition to output signal transition), less power consumption, less cost, and greater reliability.
Electromechanical relay circuits, typically being slower, consuming more electrical power to operate, costing more, and having a shorter average life than their semiconductor counterparts, benefit dramatically from Boolean simplification. Let’s consider an example circuit:
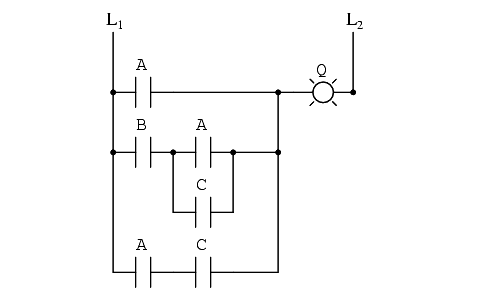
As before, our first step in reducing this circuit to its simplest form must be to develop a Boolean expression from the schematic. The easiest way I’ve found to do this is to follow the same steps I’d normally follow to reduce a series-parallel resistor network to a single, total resistance.
For example, examine the following resistor network with its resistors arranged in the same connection pattern as the relay contacts in the former circuit, and corresponding total resistance formula:
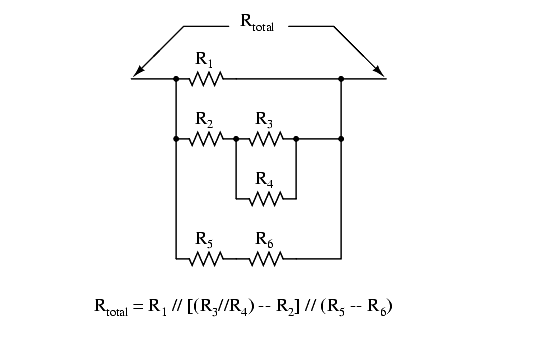 Remember that parallel contacts are equivalent to Boolean addition, while series contacts are equivalent to Boolean multiplication.
Remember that parallel contacts are equivalent to Boolean addition, while series contacts are equivalent to Boolean multiplication.
Write a Boolean expression for this relay contact circuit, following the same order of precedence that you would follow in reducing a series-parallel resistor network to a total resistance.
It may be helpful to write a Boolean sub-expression to the left of each ladder “rung,” to help organize your expression-writing:
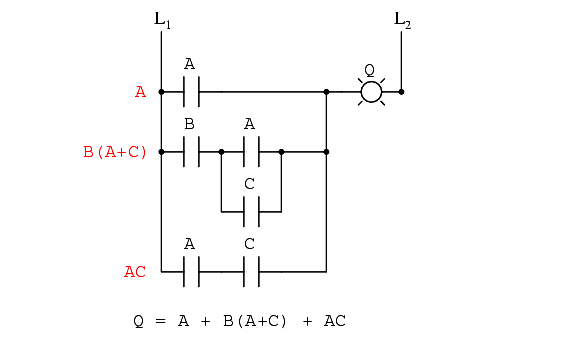 Now that we have a Boolean expression to work with, we need to apply the rules of Boolean algebra to reduce the expression to its simplest form (simplest defined as requiring the fewest relay contacts to implement):
Now that we have a Boolean expression to work with, we need to apply the rules of Boolean algebra to reduce the expression to its simplest form (simplest defined as requiring the fewest relay contacts to implement):
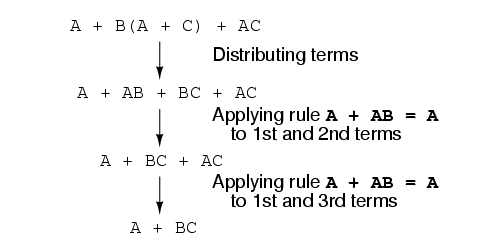 The more mathematically inclined should be able to see that the two steps employing the rule “A + AB = A” may be combined into a single step, the rule being expandable to: “A + AB + AC + AD + . . . = A”
The more mathematically inclined should be able to see that the two steps employing the rule “A + AB = A” may be combined into a single step, the rule being expandable to: “A + AB + AC + AD + . . . = A”
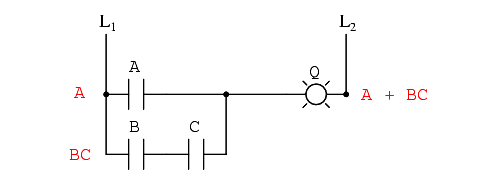
 As you can see, the reduced circuit is much simpler than the original, yet performs the same logical function:
As you can see, the reduced circuit is much simpler than the original, yet performs the same logical function:
Review
To convert a gate circuit to a Boolean expression, label each gate output with a Boolean sub-expression corresponding to the gates’ input signals, until a final expression is reached at the last gate.
To convert a Boolean expression to a gate circuit, evaluate the expression using standard order of operations: multiplication before addition, and operations within parentheses before anything else.
To convert a ladder logic circuit to a Boolean expression, label each rung with a Boolean sub-expression corresponding to the contacts’ input signals, until a final expression is reached at the last coil or light.
To determine proper order of evaluation, treat the contacts as though they were resistors, and as if you were determining total resistance of the series-parallel network formed by them. In other words, look for contacts that are either directly in series or directly in parallel with each other first, then “collapse” them into equivalent Boolean sub-expressions before proceeding to other contacts.
To convert a Boolean expression to a ladder logic circuit, evaluate the expression using standard order of operations: multiplication before addition, and operations within parentheses before anything else.
