A Resistive Temperature Detector (RTD) is a special temperature-sensing element made of fine metal wire, the electrical resistance of which changes with temperature as approximated by the following formula:
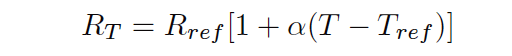
Where,
RT = Resistance of RTD at given temperature T (ohms)
Rref = Resistance of RTD at the reference temperature Tref (ohms)
α = Temperature coefficient of resistance (ohms per ohm/degree)
The following example shows how to use this formula to calculate the resistance of a “100 ohm” platinum RTD with a temperature coefficient value of 0.00392 at a temperature of 35 degrees Celsius:
RT = 100 [1 + (0.00392)(35o C − 0o C)]
RT = 100 [1 + 0.1372]
RT = 100 [1.1372]
RT = 113.72
Due to nonlinearities in the RTD’s behavior, this linear RTD formula is only an approximation. A better approximation is the Callendar-van Dusen formula, which introduces second, third, and fourth-degree terms for a better fit:
RT = Rref (1 + AT + BT2 − 100CT3 + CT4) for temperatures ranging −200 oC < T < 0 oC and
RT = Rref (1+AT +BT2) for temperatures ranging 0 oC < T < 661 oC,
both assuming Tref = 0 oC. The A, B, and C coefficients vary with the specific type of RTD, equivalent in role to α in the linear RTD formula.
Water’s melting/freezing point is the standard reference temperature for most RTDs. Here are some typical values of α for common metals:
- Nickel = 0.00672 Ω/ΩoC
- Tungsten = 0.0045 Ω/ΩoC
- Silver = 0.0041 Ω/ΩoC
- Gold = 0.0040 Ω/ΩoC
- Platinum = 0.00392 Ω/ΩoC
- Copper = 0.0038 Ω/ΩoC
As mentioned previously, platinum is a common wire material for industrial RTD construction. The alpha (α) value for platinum varies according to the alloying of the metal. For “reference grade” platinum wire, the most common alpha value is 0.003902. Industrial-grade platinum alloy RTD wire is commonly available in two different coefficient values: 0.00385 (the “European” alpha value) and 0.00392 (the “American” alpha value), of which the “European” value of 0.00385 is most commonly used (even in the United States!).
An alternative to mathematically predicting the resistance of an RTD is to simply look up its predicted resistance versus temperature in a table of values published for that RTD type. Tables capture the nuances of an RTD’s non-linearity without adding any mathematical complexity: simply look up the resistance corresponding to a given temperature, or vice-versa. If a value falls between two nearest entries in the table, you may interpolate the find the desired value, regarding the two nearest table entries as end-points defining a line segment, calculating the point you desire along that line.
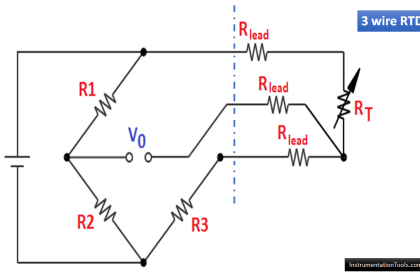
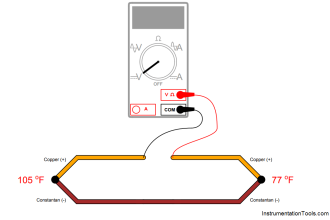
100 Ω is a very common reference resistance (Rref at 0 degrees Celsius) for industrial RTDs. 1000 Ω is another common reference resistance, and some industrial RTDs have reference resistances as low as 10 Ω . Compared to thermistors with their tens or even hundreds of thousands of ohms’ resistance, an RTD’s resistance is comparatively small. This can cause problems with measurement, since the wires connecting an RTD to its ohmmeter possess their own resistance, which will be a more substantial percentage of the total circuit resistance than for a thermistor.
Credits : Tony R. Kuphaldt – Creative Commons Attribution 4.0 License