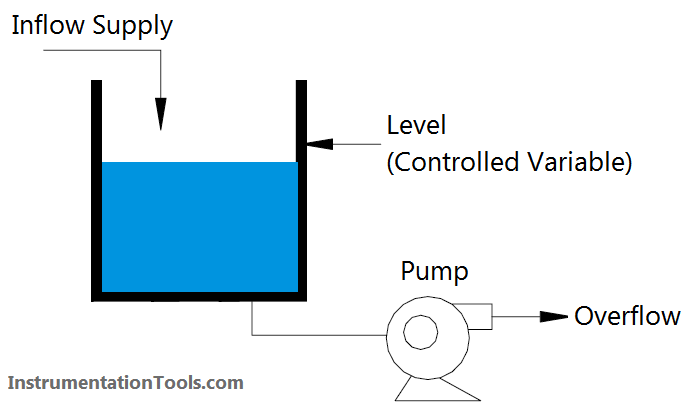
Consider a typical process control system. For a particular example let us look at an open tank, which supplies a process, say, a pump, at its output. The tank will require a supply to maintain its level (and therefore the pump’s positive suction head) at a fixed predetermined point. This predetermined level is referred to as the setpoint (SP) and it is also the controlled quantity of the system.

Clearly whilst the inflow and outflow are in mass balance, the level will remain constant. Any difference in the relative flows will cause the level to vary. How can we effectively control this system to a constant level? We must first identify our variables. Obviously there could be a number of variables in any system, the two in which we are most interested are:

The controlled variable – in our example this will be level.

The manipulated variable -– the inflow or outflow from the system.

If we look more closely at our sample system (Below Figure), assuming the level is at the setpoint, the inflow to the system and outflow are balanced. Obviously no control action is required whilst this status quo exists. Control action is only necessary when a difference or error exists between the setpoint and the measured level. Depending on whether this error is a positive or negative quantity, the appropriate control correction will be made in an attempt to restore the process to the setpoint.

Henceforth, the error will always take the form of:

Error = Setpoint – – Measured Quantity

or

e = SP – M

The control action will be either to vary the inflow or outflow from the system in order to keep the level at the setpoint. Let us consider the general format for achieving these objectives.

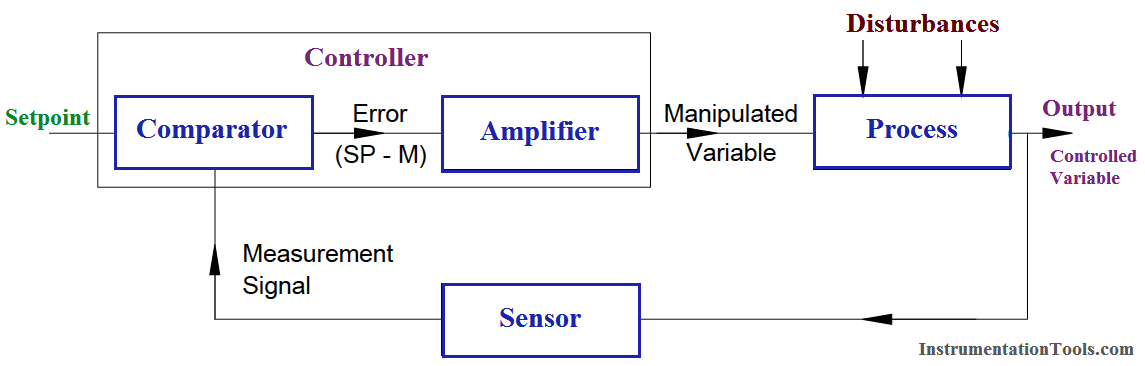
As can be seen from Below Figure, the process can be represented by a closed loop. The system output (level) is monitored by a process sensor and the measurement signal is fedback to a comparator at the input of the system. The second input to the comparator is the setpoint signal; the comparator’s output being the difference or error signal. The amplifier will provide the appropriate correction to maintain the process at its setpoint despite disturbances that may occur (Generally Amplifier is also inbuilt function of comparator/controller). It can be seen that if the system were being operated in manual control the feedback path would not be present. The operator would provide this feedback and apply the necessary correction to the system whilst observing the effect on the controlled variable. This is termed open loop operation.

Fig : Feedback Control Block Diagram

We have two types of basic control systems:

Feedback Control

This concept justifies the use of the word negative in three ways:

• The negative aspect of feeding the measured signal backwards from the output to the input of the system. (Actual definition of negative feedback control).
• The control correction must be negative in that a correction rather than a compounding of error must occur.
• The fact that an error must occur before a correction can take place, i.e., retrospective or negative control action.

Feedforward Control

If we wish to control our process without an error first occurring, we must base our control on correction of the disturbances, which will eventually, cause a process error. This is termed feedforward control. Feedforward control is rarely if ever used on its own but is used in conjunction with feedback control to improve the response of control to process disturbances.

Summary

• Controlled Variable –: output quantity of system (Level, Temperature, etc.).
• Manipulated Variable :– means of maintaining controlled variable at the setpoint.
• Error signal –: equals the difference between the setpoint and the measurement. (e = SP -– M).
• Setpoint –: desired process level. (SP)
• Measurement :– actual process level. (M)
• Closed Loop :– automatic control.
• Open Loop :– manual control.
• Feedback control is error correction following a disturbance.
• Feedforward control is control of disturbances, which could cause a process error.

Also Read :

• On/Off Controller Principle
• Proportional Controller Principle
• Integral Controller Principle
• Derivative Controller Principle