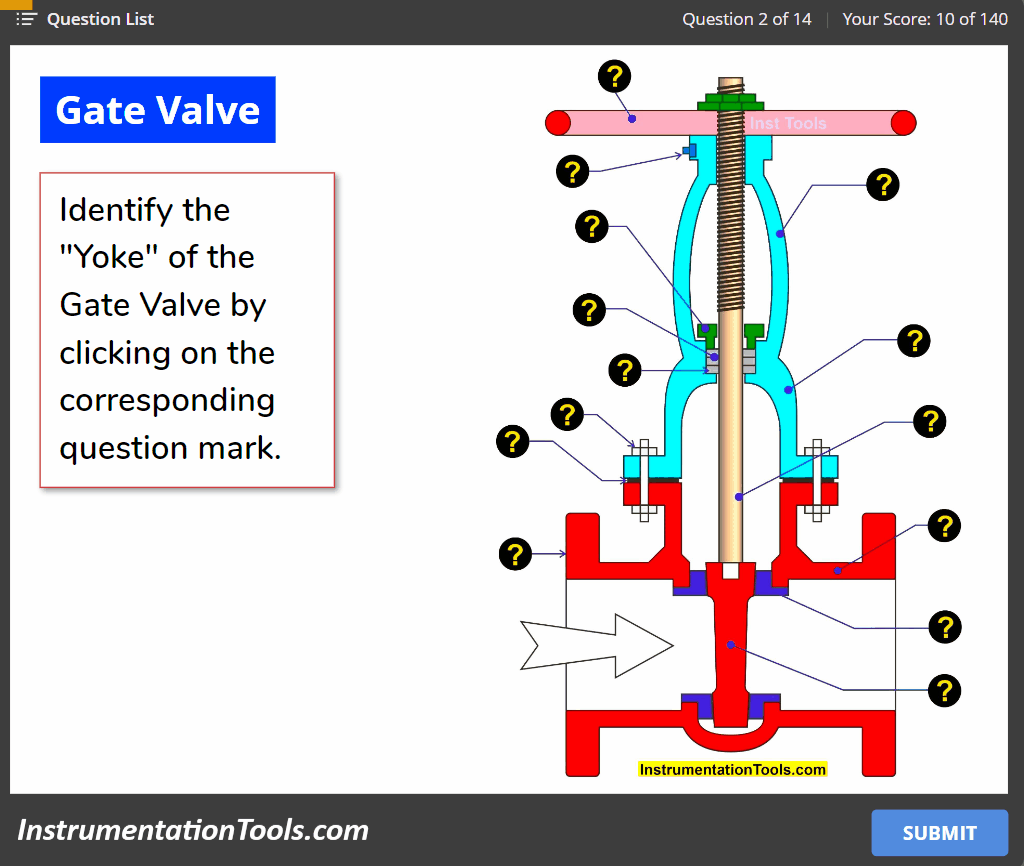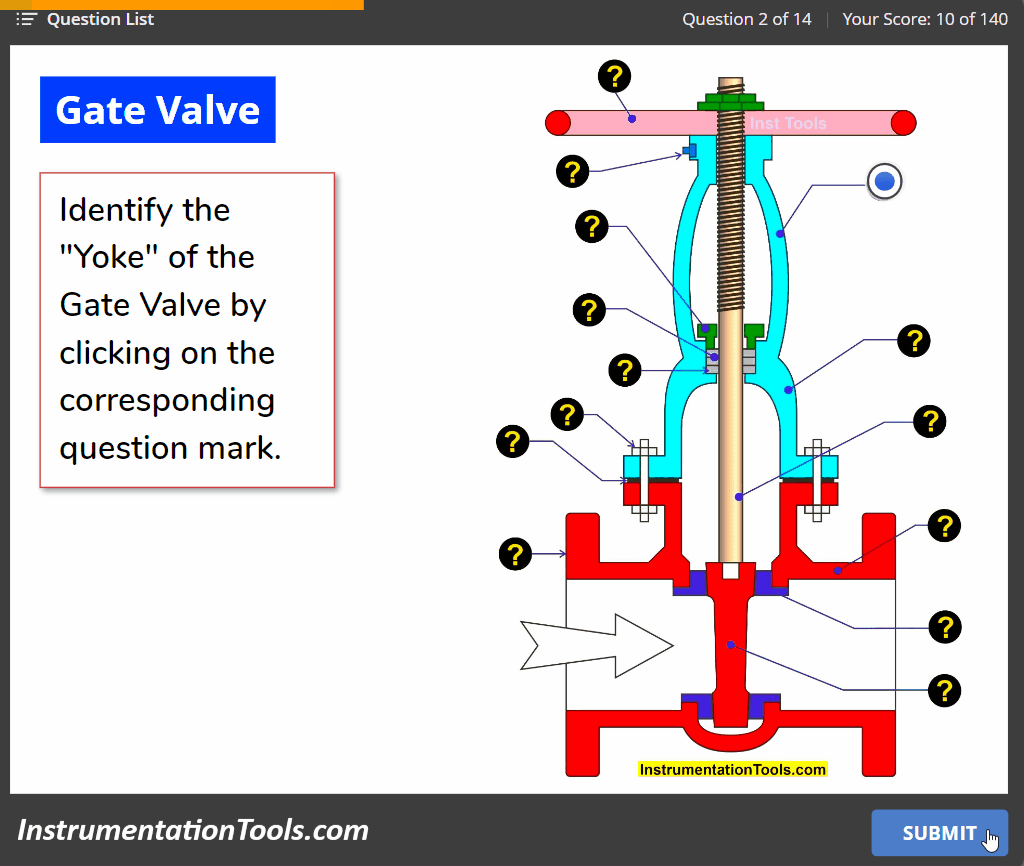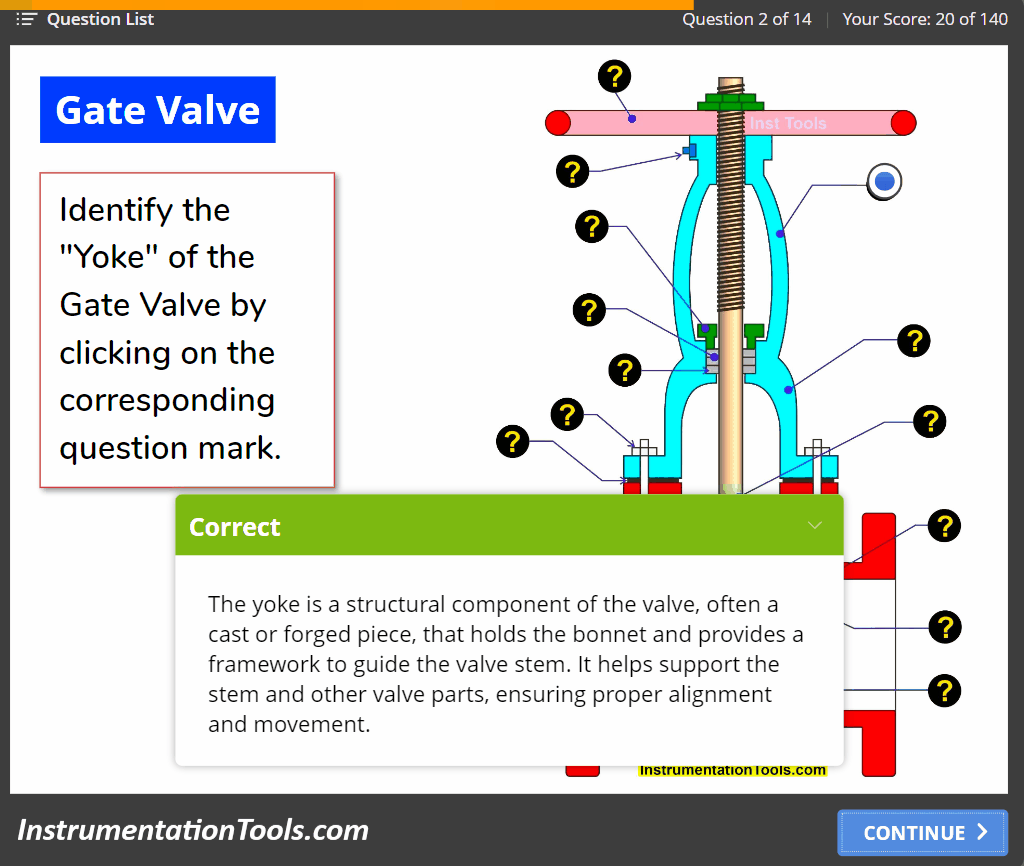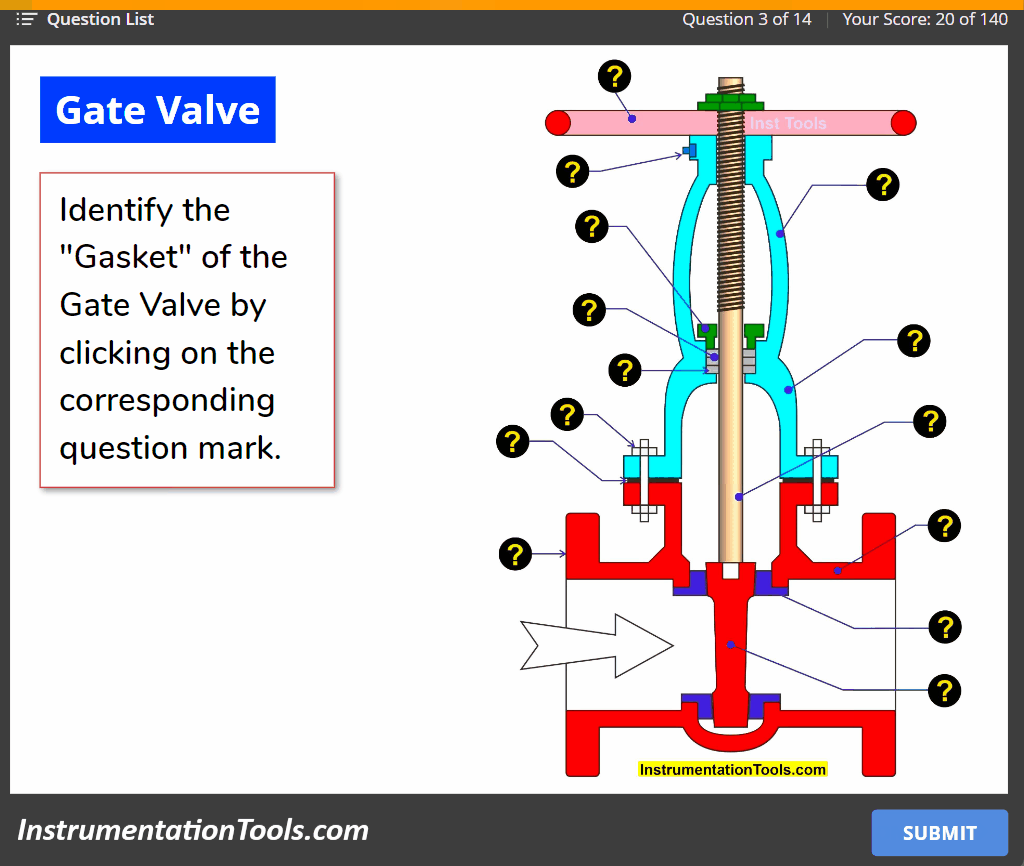
Effect of Adding a Zero to a System
1. Assertion (A): The zeroes on the real axis near the origin are generally avoided in design.
Reason (R): In a sluggish system introduction of zeroes can improve the transient response
a) Both A and R are true and R is correct explanation of A
b) Both A and R are true but R is not correct explanation of A
c) A is true but R is false
d) A is false but R is true
Answer: b
Explanation: Zero is defined as the root of the numerator of the transfer function and zero is to introduce a pronounced peak to the system’s response whereby the peak overshoot may increase appreciably.
2. Addition of zero increases the stability.
a) True
b) False
Answer: a
Explanation: Zero is defined as the root of the numerator of the transfer function and addition of zeroes increases the stability as the speed of response increases.
3. Zeroes are defined as:
a) Roots of the denominator of the closed loop transfer function
b) Roots of the numerator of the closed loop transfer function
c) Parts of the numerator
d) Parts of the denominator
Answer: b
Explanation: Zeroes are the roots of the numerator of the closed loop system and addition of the zeroes increases the stability of the closed loop system.
4. As zero moves sufficiently left from the origin the effect of zero becomes less pronounced.
a) True
b) False
Answer: a
Explanation: The effect of zero on transient response will be negligible if the zero moves left from the origin as the zero which is nearer to the origin is more dominant.
5. If number of poles are greater than number of zeroes then the system is known as ______________
a) Stable system
b) Unstable system
c) Minimum phase system
d) Non-minimum phase system
Answer: c
Explanation: Minimum phase system is defined as the perfect system with zeroes greater than poles and also the zeroes and poles lying on the left half of the s plane entirely.
6. A control system is generally met with the time response specifications:
a) Steady state accuracy
b) Damping factor
c) Setting time
d) All of the mentioned
Answer: d
Explanation: Steady state error, damping factor and settling times are the specifications are needed to control the system’s stability and speed of response.
7. Steady state accuracy specified in terms of:
a) Steady state error
b) Damping ratio
c) Natural frequency
d) All of the mentioned
Answer: a
Explanation: Steady state accuracy entirely depends on the accuracy of steady state which is determined by steady state error which is the difference between the final output and desired output.
8. Steady state accuracy is determined by suitable choice of____________
a) Steady error
b) Error constants
c) Damping
d) Transient error
Answer: b
Explanation: Steady state accuracy is determined by suitable choice of error constants Kv, Kp and Ka depending upon the type of the system.
9. Damping factor specifies:
a) Peak overshot to step input.
b) Steady state error
c) Damping ratio
d) Natural frequency
Answer: a
Explanation: Maximum peak overshoot is the maximum peak of the transient response at the resonant frequency and is so calculated as to determine the value of damping factor.
10. If rise time is also taken into consideration it should be ____________ to the settling time.
a) Inconsistent
b) Consistent
c) Perfect
d) Unique
Answer: b
Explanation: Rise time and settling time determine the speed of response as if the values of both these if less then the speed of response will be more and both of these depend on the damping factor and natural frequency.