Bimetallic Thermometer

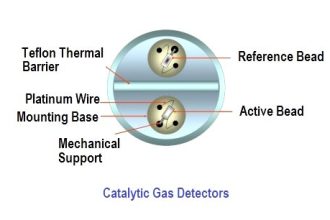
A bimetallic strip is made up of metal A and B, having different thermal expansion co-efficient. It is bonded together.

These thermometers use the following two principles:

1. All metals change in dimension, that is expand or contract when there is a change in temperature.

2. The rate at which this expansion or contraction takes place depend on the temperature co-efficient of expansion of the metal and this temperature coefficient of expansion is different for different metals.Hence the difference in thermal expansion rates is used to produce deflections which is proportional to temperature changes.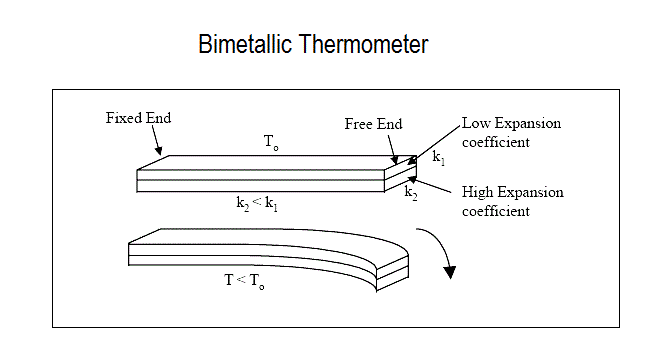The bimetallic thermometer consists of a bimetallic strip. A bimetallic strip is made of two thin strips of metals which have different coefficients of expansion. The two metal strips are joined together by brazing, welding or reveting so that the relative motion between them is arrested.

Fig : A bimetallic coil from a thermometer reacts to the heat from a lighter, by uncoiling and then coiling back up when the lighter is removed.

The bimetallic strip is in the form of a cantilever beam. An increase in temperature will result in the deflection of the free end of the strip as shown i diagram. This deflection is linear and can be related to temperature changes.

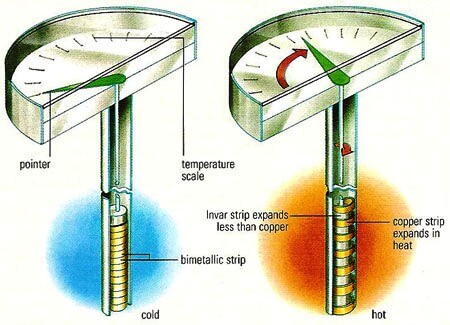
Image Credits : daviddarling.info

The radius of the curvature of the bimetallic strip which was initially flat is determined using the following relationship.

R= t{3(1+m)² + (1+mn)[m²+1/mn]}/6(άh-άl)(T2-T1)(1+m) ²

where,

R= radius of the curvature at the temperature T2.
T = total thickness of the bimetallic strip = (t1+t2)
m=t1/t2 = Thickness of lower – expansion metal/thickness of higher – expansion metal.
άl= coefficient of expansion of lower expansion metal.
άh= coefficient of expansion of higher expansion metal.
T1 = Initial temperature.
T2 = temperature.

Let us consider the case of a bimetallic strip in the form of a cantilever of length L as shown in fig. And α_A, α_B is the thermal co-efficient of expansion of metal A and metal B.

The strip is assumed to bend through a circular arc when subjected to a change in temperature. The thickness of each metal forming the strip is t/2.

Therefore,

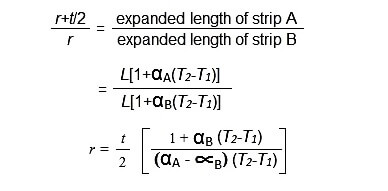
In case one of the metals has a very low thermal expansion co-efficient say B, we have α_B≈ 0.

Therefore,

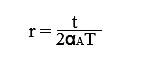
From the above relation it is clear that if one end of the bimetallic strip is fixed, the deflection of the free end is a direct indication of the temperature of strip.

The following are the important properties a material should have to be selected for bimetallic thermometers.

1. Coefficient of expansion.
2. Modulus of elasticity.
3. Elastic limit after cold rolling.
4. Electrical conductivity.
5. Ductility.
6. Metallurgical ability.

Different common forms of bimetallic sensors are listed.

1. Helix type.
2. Spiral type.
3. Cantilever type.
4. Flat type.

Metals used in bimetallic strips are:

1. High expansion

• Brass
• Nickel-iron alloyd with chromium & manganese.

2. Low Expansion

• Invar (alloy of nickel & iron).

Application of bimetallic strips and thermometers

1. The bimetallic strip is used in control devices.
2. The spiral strip is used in air conditioning thermostats.
3. The helix strip is used for process application such as refineries, oil burners, tyre vulcanisers etc.,

Advantages of bimetallic thermometers

1. They are simple, robust and inexpensive.
2. Their accuracy is between +or- 2% to 5% of the scale.
3. They can with stand 50% over range in temperaures.
4. They can be used where ever a mercury–in-glass thermometer is used.

Limitations of bimetallic thermometer

1. They are not recommended for temperature above 400’C.
2. When regularly used, the bimetallic may permanently deform, which in turn will introduce errors.