Controllability & Observability
1. A system is said to be_____________ if it is possible to transfer the system state from any initial state to any desired state in finite interval of time.
a) Controllable
b) Observable
c) Cannot be determined
d) Controllable and observable
Answer: a
Explanation: By definition a system is said to be controllable, if it is possible to transfer the system state from any initial state to any desired state in finite interval of time.
2. A system is said to be_________________ if every state can be completely identified by measurements of the outputs at the finite time interval.
a) Controllable
b) Observable
c) Cannot be determined
d) Controllable and observable
Answer: b
Explanation: By definition, a system is said to be observable, if every state can be completely identified by measurements of the outputs at the finite time interval.
3. Kalman’s test is for :
a) Observability
b) Controllability
c) Optimality
d) Observability and controllability
Answer: d
Explanation: Kalman’s test is the test that is done for the controllability and observability by solving the matrix by kalman’s matrix individually for both tests.
4. Consider a system if represented by state space equation and x1 (t) =x2 (t), then the system is:
a) Controllable
b) Uncontrollable
c) Observable
d) Unstable
Answer: b
Explanation: After calculating the matrix which for controllable system and finding the determinant and should not be zero but in this case comes to be zero.
5. For the system,
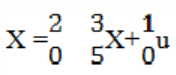
which of the following statements is true?
a) The system is controllable but unstable
b) The system is uncontrollable and unstable
c) The system is controllable and stable
d) The system is uncontrollable and stable
Answer: b
Explanation: By Kalman’s stability test the system is uncontrollable and root of the characteristic equation lies on the right side of the s-plane.
6. A transfer function of the system does not have pole-zero cancellation? Which of the following statements is true?
a) System is neither controllable nor observable
b) System is completely controllable and observable
c) System is observable but uncontrollable
d) System is controllable and unobservable
Answer: b
Explanation: If the transfer function of the system does not have pole-zero cancellation then it is completely controllable and observable.
7. Complex conjugate pair:
a) Center
b) Focus point
c) Saddle point
d) Stable node
Answer: b
Explanation: Complex conjugate pair is the complex pair of the roots of the equation and has a focus point.
8. Pure imaginary pair:
a) Centre
b) Focus point
c) Saddle point
d) Stable node
Answer: a
Explanation: Pure imaginary pair is the nature of the root of the equation that has no real part only has the nature of center for linearized autonomous second order system.
9. Real and equal but with opposite sign.
a) Center
b) Focus point
c) Saddle point
d) Stable node
Answer: c
Explanation: Saddle point are real and equal with opposite sign and these points are called the saddle point as the points are different with real and equal with opposite sign.
10. Real distinct and negative.
a) Center
b) Focus point
c) Saddle point
d) Stable node
Answer: d
Explanation: Stable node is real distinct and negative and this node is stable as the points or roots are real and neative lying on the left side of the plane.